Curso de R:
Capitulo 8: Más ejemplos de Regresión Lineal.
En este capítulo nos vamos a centrar en ver más ejemplos de regresión y en ver las posibilidades gráficas que tiene R al respecto, las posibilidades que son todas las que se quieran ya que como hemos visto en capítulos anteriores es muy fácil programar tus própios análisis estadísticos. Digo esto por si alguien no está acostumbrado a seguir una metodología distinta a la hora de realizar los modelos. Además el programar tus propios métodos hace que puedas comprender mejor las salidas por pantalla y los pasos que sigue el programa. En el primer ejemplo que vamos a ver partimos del ejemplo 7.2 del capítulo 7 que si recordamos era un modelo de regresión múltiple donde teníamos problemas de multicolinealidad.
Ejemplo 8.2:
Si recordamos en el ejemplo 7.2 nos pedían que hicieramos un modelo para predecir las notas finales a partir de las notas de los exámenes previos, el test y la puntuación del laboratorio. Teníamos una variable dependiente que era la nota final y cuatro variables regresoras. Vimos que el modelo presentaba múltiples lagunas (multicolinealidad, un modelo con un r cuadrado bajo,...). Pues ahora nos piden mejorar el modelo. Es difícil mejorarlo en precisión porque no tenemos más variables regresoras en el conjunto de datos por eso podemos mejorarlo haciéndolo más sencillo y recogiendo una cantidad de información lo más grande posible con un modelo lo más reducido posible, es decir, vamos a seleccionar un modelo de regesión. Para hacer esto contamos con la función step que selecciona un modelo de regresión a partir del criterio de información de Akaike (AIC, siglas en inglés). Creamos un estadístico que permite decidir el orden de un modelo. AIC toma en consideración tanto la medida en que el modelo se ajusta a las series observadas como el número de parámetros utilizados en el ajuste. Búscamos el modelo que describa adecuadamente las series y tenga el mínimo AIC. Veamos como lo presenta R:
> modelo8.1<-lm(final~test+exam1+exam2+labo,data=archivo) #modelo lineal
> step(modelo8.1,direction="forward") #seleccionamos hacia delante
Start: AIC= 303.37
final ~ test + exam1 + exam2 + labo
Df Sum of Sq RSS AIC
- labo 1 99.2 19612.9 301.6
- test 1 561.2 20074.9 302.8
- exam2 1 614.5 20128.2 302.9
<none> 19513.7 303.4
- exam1 1 3429.8 22943.5 309.3
Step: AIC= 301.61
final ~ test + exam1 + exam2
Df Sum of Sq RSS AIC
- exam2 1 661.8 20274.7 301.2
<none> 19612.9 301.6
- test 1 1645.0 21258.0 303.6
- exam1 1 3601.0 23213.9 307.9
Step: AIC= 301.24
final ~ test + exam1
Df Sum of Sq RSS AIC
<none> 20274.7 301.2
- test 1 2511.8 22786.5 305.0
- exam1 1 5469.7 25744.4 310.9
Call:
lm(formula = final ~ test + exam1, data = archivo)
Coefficients:
(Intercept) test exam1
25.9520 1.3026 0.7172
|
La forma que tiene de trabajar R parece bastante comprensible pero en mi caso estoy más acostumbrado a emplear el método forward de otro modo. Primero selecciono la variable candidata a entrar (la que mayor coeficiente de correlación lineal tenga con la variable dependiente) y posteriormente busco la variable que menor suma del cuadrado del error me produzca y después contrastamos si esa variable debe permanecer en el modelo. R lo que hace es marcar un AIC referencia y entran en el modelo todas las variables que tengan mayor AIC que ese valor referencia. En este caso por este método el modelo sería final=1.3test+0.71exam1, sólo se ha quedado con dos variables regresoras.
Veamos este modelo como sería:
> modelo.FINAL<-lm(final~test+exam1,data=archivo) > summary(modelo.FINAL,cor=T) #incluimos cor=T para ver la correlación de los coeficientes Call: lm(formula = final ~ test + exam1, data = archivo) Residuals:
Min 1Q Median 3Q Max
-72.627 -12.149 2.902 16.257 34.708
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 25.9520 20.3937 1.273 0.209573
test 1.3026 0.5457 2.387 0.021143 *
exam1 0.7172 0.2036 3.523 0.000977 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 20.99 on 46 degrees of freedom Multiple R-Squared: 0.451, Adjusted R-squared: 0.4271 F-statistic: 18.89 on 2 and 46 DF, p-value: 1.024e-06 Correlation of Coefficients:
(Intercept) test
test -0.7179
exam1 -0.1935 -0.5326
|
Ahora imaginemos que nos interesa ver como funciona el modelo final de dos variables regresoras; si cumple las hipótesis (media del error 0, homocedasticidad, incorrelación, distribución normal del error). Esto fundamentalmente se puede ver de forma gráfica, las funciones R son muy sencillas, veámoslas:
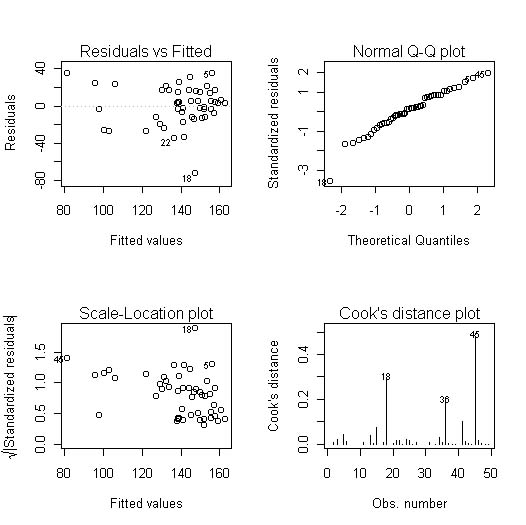
> par(mfrow = c(2,2)) #con esto ponemos los 4 gráficos en la misma ventana > plot(modelo.FINAL) #pedimos los gráficos del modelo |
Obteniendo en la ventana de gráficos:

Figura 1
Parece que el modelo presenta heterocedasticidad como vemos en el gráfico de residuos studentizados frente a las predicciones y también vemos como hay algunas observaciones (las número 18, 36 y 45) que podrían ser potencialmente influyentes como nos indica el gráfico de las distancias de Cook Sin embargo el modelo si cumple las hipótesis de media 0 y distribución normal de los residuos.
La distancia de Cook del caso i-ésimo consiste en buscar la distancia entre los parámetros estimados si incluyen la observación i-ésima y si no la incluyen. Cada observación tiene su distancia y se considera significativa si es mayor que 1. Esta distancia se calcula con R con la función cooks.distance(objeto):
> cook<-cooks.distance(modelo.FINAL)
> significativas<-cook>1
> significativas
1 2 3 4 5 6 7 8 9 10 11 12 13
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
14 15 16 17 18 19 20 21 22 23 24 25 26
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
27 28 29 30 31 32 33 34 35 36 37 38 39
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
40 41 42 43 44 45 46 47 48 49
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
|
He creado el vector cook con las distancias y después el vector significativas que recoge una variable lógica. Como vemos ninguna observación supera el valor referencia 1, ninguna observación es potencialmente influyente. Otra forma de ver si una observación es potencialmente influyente es ver el potencial que tiene el caso i-ésimo, el peso que tiene la observación i-ésima a la hora de estimar la predicción. Si el potencial de una observación es alto tiene mucho peso a la hora de dar la predicción. Estos potenciales se obtienen matricialmente como la diagonal principal de la matriz HAT que se calcula a partir de la matriz de diseño del modelo que es la matriz de datos con la 1ª columna de unos. Hat es H, X es la matriz de diseño: H=X(X'X)-1X'. La matriz de diseño se crea con la función model.matrix(objeto) y hat se crea a partir de esta matriz de diseño. Los elemento de la diagonal principal de hat son los potenciales sobre los que continuamos nuestro estudio:
> matriz.modelo<-model.matrix(modelo.FINAL) #creamos la matriz de diseño > potenciales<-hat(matriz.modelo) > potenciales<-hat(matriz.modelo) #creamos potenciales que contiene la matriz hat del modelo > plot(potenciales) #hacemos un gráfico de potenciales para ver los mayores > identify(potenciales) #identificamos sobre el gráfico el nº de la observación |
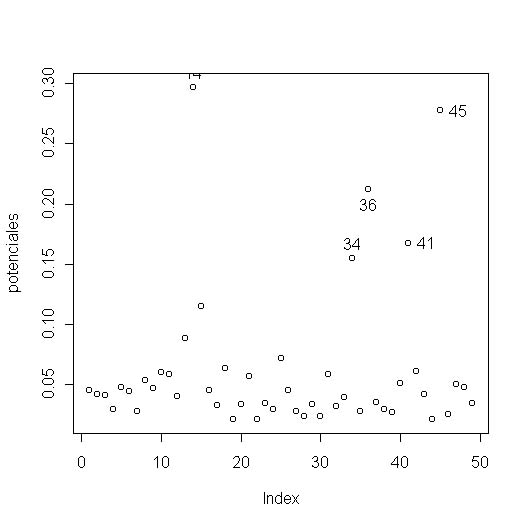
Esas son las observaciones con unos potenciales más altos, nos interesa que las observaciones tengan un potencial similar de aproximadamente el cociente de las variables regresoras (más uno por la columna de unos de X) entre el número de observaciones. Si se dobla esta cantidad estaríamos ante casos que hay que estudiar con detalle. Si además miramos el gráfico de las distancias de Cook (Figura 1) vemos que las observaciones problemáticas son la número 45 y 36. Estos casos podían influir en nuestro modelo.
Capítulo
9: Análisis de Componentes
Principales.