Capítulo 5: Inferencia estadística

En este capítulo voy a hacer memoria y recordar algunos términos y conceptos básicos de estadística. En primer lugar hacemos inferencia a partir de unas observaciones obtenidas a partir de la población a las que vamos a extraer unas propiedades que se denominan estadísticos muestrales. Además vamos a conocer la distribución de dichos estadísticos (generalmente distribución normal) por lo que hacemos inferencia paramétrica.

La inferencia paramétrica puede recogerse en una vertiente o en otra según el parámetro a estimar; tenemos por un lado la estadística clásica (que es en la que nos vamos a centrar) y por otro lado la estadística ballesiana.

Tenemos un experimento, lo repetimos varias veces y obtenemos una muestra con variables aleatorias independientes idénticamente distribuidas con función de distribución conocida. (Por ejemplo tenemos las alturas de 30 varones españoles y estimo que la altura media de los españoles es 1,77 estamos ante una estimación puntual). Pues cualquier función de la muestra que no dependa del parámetro a estimar es un estadístico y aquel estadístico que se utiliza para inferir sobre el parámetro desconocido es un estimador. Ejemplos de estadísticos son el total muestral, la media muestral, la varianza muestral, la cuasivarianza muestral, los estadísticos de orden,...

Conocemos los conceptos básicos para comenzar a trabajar, también sabemos que las observaciones del experimento generalmente tienen distribución normal (esto es inferencia paramétrica). Ahora bien, necesitamos determinar unas distribuciones en el muestreo que estén asociadas con la distribución normal. Estas distribuciones son la chi-cuadrado, la t de Student y la F de Snedecor.

"La chi-cuadrado es una suma de normales al cuadrado" más o menos se podía definir así ya que si calculamos la distribución de una variable normal al cuadrado no podemos aplicar cambio de variable y a partir de su función de distribución llegamos a una función de densidad de una gamma con parámetros 1/2 y 1/2 que es una chi-cuadrado con 1 grado de libertad. La gamma es reproductiva respecto al primer parámetro por lo que sumas de normales (0,1) nos proporcionan gammas de parámetros n/2 y 1/2 o lo que es lo mismo chi-cuadrado con n grados de libertad.

La t de Student se crea a partir de una normal (0,1) y una chi-cuadrado con n grados de libertad independientes. Una variable se distribuye bajo una t de Student si se puede definir como normal(0,1) dividido por la raíz cuadrada de una chi-cuadrado partida por sus grados de libertad; difícil de comprender así mejor veamos un ejemplo:

La F de Snedecor se crea a partir de dos chi-cuadrado independientes dividivas por sus respectivos grados de libertad, así la F de Snedecor tiene dos parámetros que indican sus grados de libertad:

Me dejo en el tintero muchos aspectos como las distribuciones de los estadísticos o los métodos de construcción de contrastes e intervalos pero me podría extender mucho, y me extenderé pero hasta aquí os cuento de momento. Aun así recomendaros una bibliografía básica por si queréis profundizar más en el tema. También estoy a expensas de poder publicar archivos LaTeX para que los aspectos matemáticos queden mejor resueltos pero de momento conformaros con los ejemplos de más abajo.

Bueno pues comencemos con R, la función que nos ofrece tanto estimaciones puntuales como intervalos de confianza como contrastes de hipótesis es:

> t.test (datos_x, datos_y =NULL, alternative = "two.sided", mu = 0,

 paired =FALSE, var.equal = FALSE, conf.level= 0.95)

Las opciones indicadas son todas las ofrecidas por defecto. Podemos poner sólo un conjunto de datos para muestras unidimensionales (estimaciones puntuales) los dos conjuntos para comparación de muestras.

El argumento alternative indica el tipo de contraste, bilateral two.sided, si la hipótesis alternativa es mayor (Ho: menor o igual) se utiliza greater, si la hipótesis alternativa es menor (Ho: mayor o igual) entonces se usa less.

En paired=T estamos ante una situación de datos no apareados para indicar que estamos ante datos apareados poner paired=F.

Con var.equal estamos estamos trabajando con los casos de igualdad o no de varianzas que sólo se emplean en comparación de dos poblaciones. Si var.equal=T las varianzas de las dos poblaciones son iguales si var.equal=F las varianzas de ambas poblaciones no se suponen iguales.

Por último tenemos el argumento conf.level en el que indicamos el el nivel de confianza del test.

Si deseáramos hacer el contraste para la igualdad de varianzas (cociente de varianzas=1) habríamos de emplear la función var.test:

Con objeto de estimar la altura de los varones españoles menores de 25 años se recogió una muestra aleatoria simple de 15 individuos que cumplían ese requisito. Suponiendo que la muestra se distribuye normalmente determinar un intervalo de confianza al 95% para la media.

Tenemos una variable con distribución normal de media y desviación típica desconocidas por ello el intervalo de confianza ha de ser:

> alturas<-scan()

1: 1.77 1.80 1.65 1.69 1.86 1.75 1.58

8: 1.79 1.76 1.81 1.91 1.78 1.80 1.69 1.81 

16: 

Read 15 items

> t.test(alturas)

        One Sample t-test

data:  alturas 

t = 82.3296, df = 14, p-value = < 2.2e-16

alternative hypothesis: true mean is not equal to 0 

95 percent confidence interval:

 1.717396 1.809270 

sample estimates:

mean of x 

 1.763333

El intervalo es [1.71,1.80]. La función t.test no tiene ningún argumento opcional puesto que los necesarios son los que recoge por defecto. Ahora imaginemos que lo que queremos es estimar si la altura media de los españoles es de 1.77 metros hay que introducir algunas modificaciones:

> t.test(alturas,mu=1.77)

        One Sample t-test

data:  alturas 

t = -0.3113, df = 14, p-value = 0.7602

alternative hypothesis: true mean is not equal to 1.77 

95 percent confidence interval:

 1.717396 1.809270 

sample estimates:

mean of x 

 1.763333

Como se puede ver p-value = 0.7602 indica que con un nivel de significación del 5% se acepta la hipótesis de que las altura media de los españoles es de 1.77 metros.

El director de una sucursal de una compañía de seguros espera que dos de sus mejores agentes consigan formalizar por término medio el mismo número de pólizas mensuales. Los datos de la tabla adjunta indican las pólizas formalizadas en los últimos cinco meses por ambos agentes.

Agente A	Agente B
12	14
11	18
18	18
16	17
13	16

Admitiendo que el número de pólizas contratadas mensualmente por los dos trabajadores son variables aleatorias independientes y distribuidas normalmente: ¿Tiene igual varianza? ¿Se puede aceptar la hipótesis del director de la sucursal en función de los resultados de la tabla y a un nivel de confianza del 99%?

> agente_A<-c(12,11,18,16,13)

> agente_B<-c(14,18,18,17,16)

> var.test(agente_A,agente_B)

        F test to compare two variances

data:  agente <- A and agente <- B 

F = 3.0357, num df = 4, denom df = 4, p-value = 0.3075

alternative hypothesis: true ratio of variances is not equal to 1 

95 percent confidence interval:

  0.3160711 29.1566086 

sample estimates:

ratio of variances 

          3.035714

Los datos recogidos tienen igual varianza ya que no se rechaza la hipótesis de igualdad de varianzas. Como los datos están distribuidos normalmente y las varianzas son iguales los agentes harán la misma cantidad de pólizas si la diferencia de sus medias es estadísticamente distinta de 0, esta es la hipótesis de partida. Esta hipótesis de rechaza cuando:

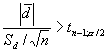
> t.test (agente_A,agente_B, paired=T, conf.level=0.99)

        Paired t-test

data:  agente <- A and agente <- B 

t = -2.1518, df = 4, p-value = 0.09779

alternative hypothesis: true difference in means is not equal to 0 

99 percent confidence interval:

 -8.163151  2.963151 

sample estimates:

mean of the differences 

                   -2.6

Por poco pero se puede aceptar la hipótesis nula ya que el p-value = 0.09779 es superior al 0.01 que establecimos de partida.