Curso de R:
Capitulo 11: Análisis de conglomerados (cluster) II.
En este capítulo vamos a ver un par de ejemplos más de análisis de conglomerados con R. En el ejemplo del capítulo 10 partíamos de un conjunto de una sola variable que era la primera componente principal de un conjunto de datos que recogía características técnias de una serie de coches que se vendían es Estados Unidos, ahora vamos a ver dos ejemplo más donde tabajaremos con otras posibilidades de R.
Ejemplo 11.1:
En este ejemplo vamos a trabajar con los datos de inflación de países de la Unión Europea. Los datos obtenidos a través de la página web del Instituto Nacional de Estadística de España vienen recogidos en un archivo excell, desconozco si existe algún paquete que me permita importar datos de excel a R (si lo hay para importar archivos SAS y SPSS), podemos trabajar con ficheros de texto pero al tratarse de 15 países y 3 variables (país, índice e incremento interanual) me parece más adecuado el introducirlos directamente en R creando tres vectores y uniéndolos de la forma más apropiada:
> nombres<-c("Alemania","Austria","Bélgica","España","Finlandia","Francia","Grecia","Holanda""Irlanda","Italia","Luxemburgo","Portugal","Dinamarca","Reino Unido","Suecia")
> indices<-scan() #indice de precios al consumo
|
En este ejemplo vamos a separar los países inflacionistas de los no inflacionistas, ese va a ser nuestro objetivo, por ello partimos de un número predeterminado de cluster en este caso 2 (inflacionistas y no inflacionistas, insisto) y asignamos a cada individuo a un cluster mediante una técnica de ubicación iterativa a esta técnica se la conoce como el algoritmo de las k-medias. Pretendemos mejorar las clasificaciones minimizando las distancias utilizadas en la formación de los conglomerados. Sería siempre interesante empezar por la aglomeración jerárquica pero en este caso el objetivo de nuestro agrupamiento parece bastante claro y no es necesario comprobar cuantos cluster se pueden formar.
El siguiente paso con R es unir los dos vectores que contienen
datos numéricos para formar el conjunto de datos sobre el que vamos a
calcular la matriz de distancias con la que posteriormente realizaremos el análisis
de agrupamiento. En este caso el método de cálculo de la matriz
de distancias es el método Manhattan ![]() que
se utiliza habitualmente en variables dicotómbicas pero para que sigais
conociendo posibilidades vamos a trabajar con ella:
que
se utiliza habitualmente en variables dicotómbicas pero para que sigais
conociendo posibilidades vamos a trabajar con ella:
> datos.inflacion<-cbind(indices,tasa) > matriz11.1<-dist(datos.inflacion,method="manhattan") |
Veamos el gráfico de dispersión para identificar visualmente algún cluster:
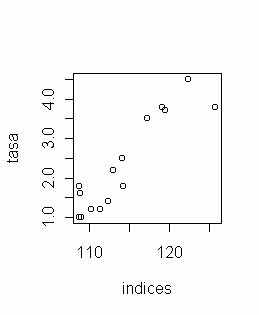
Si se identifican los cluster, arriba a la derecha tenemos los países con mayor tasa y abajo a la izquierda los de menor tasa de acumulación, ahora sólo nos queda plasmar esta idea inicial en R y ver la forma de agrupamiento de los países. Para realizar el algoritmo de las k-medias R dispone de la función kmeans(<matriz_distancias>,<num_cluster>), donde ambos argumentos son obligatorios ya que el número de cluster está prefijado:
> kmeans(matriz11.1,2) $centers (2) $withinss
[1] 545.6604 591.0740
$size (3)
[1] 10 5
|
Esto es lo que no ofrece R. en (1) tenemos a que cluster se une cada observación, en (2) las distancias de cada observación al cluster y en (3) el tamaño de cada cluster. También aparece una función withinss que no sé para que sirve pero que ahí está, si alguien lo averigua que por favor me mande un correo. Ahora nos queda ver a que cluster pertenece cada país para ello unimos el vector nombres que creamos con anterioridad con la variable $cluster de el análisis, también unimos tasa e indices para ver mejor como funciona:
> kmedias<-kmeans(matriz11.1,2) > cbind(nombres,kmedias$cluster,tasa,indices) |
Los menos inflacionistas los ha clasificado en el cluster 1 y los más inflcionistas como Holanda, Portugal,... y por supuesto mi querida España en el cluster 2. Si quisieramos ver este análisis de forma gráfica emplearíamos la función plot a la que la incluiremos unos argumentos para reconocer los cluster visualmente:
> plot(datos.inflacion,col=kmedias$cluster,pch=17,main="Agrupamiento") |
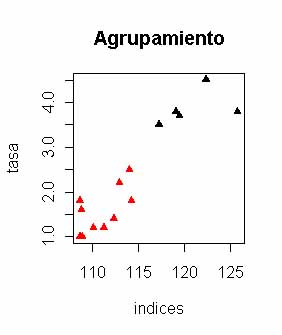
En plot los argumentos que he añadido son los colores que van unidos al cluster asignado, el tipo de de símbolo que se cambia con pch (de 1 a 18) y el título con main, por lo demás comprobar que observaciones se unen con los cluster, si se quieren identificar sólo hay que emplear la función identify que ya vimos en un capítulo anterior.
Ejemplo 11.2:
En este ejemplo vamos a agrupar distintos tipos de alimentos según sus aportes en calorías, proteínas, grasas y calcio. El conjunto de datos está en mi disco duro como un archivo de texto en el directorio datos (haz click aquí para ver el archivo) hemos de emplear la función read.table para importar el archivo a R:
> alimentos<-read.table("c:\\datos\\alimentos.txt",header=TRUE)
|
Hay que reseñar el hecho de que para leer variables alfanuméricas no podemos tener espacios en blanco ya que la función read.table podía darnos problemas, para poder poner espacios en blanco en las variables alfanuméricas hay que dar un formato de entrada que todavía no hemos visto, por eso recomiendo siempre un vistazo previo al conjunto de entrada para evitar problemas. Como podéis ver en mi caso las observaciones de la variable Alimentos no tienen espacios en blanco y he juntado palabras para evitar estos problemas. es posible leer datos en blanco, leer archivos con diferentes delimitadores, cambiar el punto decimal por coma,... pero esto lo veremos en posteriores capítulos.
Ya tenemos el conjunto de datos con el que vamos a trabajar, como siempre tenemos la pega de que este conjunto tiene una variable caracter y a la hora de realizar cálculos sobre él nos puede plantear trastornos por eso hemos de separar la variable Alimentos o como suelo hacer yo unir el resto de variables (Calorías, Proteínas, Grasas y Calcio) en una matriz con la función cbind:
> attach(alimentos) |
Ya podemos empezar a realizar nuestra labor matemática que en este caso vamos a emplear para el agrupamiento las medidas de disimilitud con base en la distancia euclidea pero que son todo lo contrario a las medidas de similitud que empleamos para los anteriores ejemplos, para hacer este ejemplo hemos de cargar la librería cluster:
> library(cluster) Metric : euclidean
Number of objects : 12
|
Esa es la matriz de disimilaridades entre los valores de las observaciones que calcula R, a partir de ella vamos a hacer el agrupamiento, vamos a ver gráficamente el comprotamiento de ese agrupamiento y posteriormente determinaremos el número de cluster necesarios para llevar a buen puerto nuestro estudio:
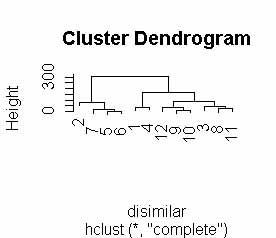
> cluster11.2<-hclust(disimilar) |
 |
> data.frame(alimentos$Alimentos,cluster11.2$order) |
Es bastante claro que tenemos dos cluster, por un lado están las observaciones 2, 7, 5, 6 y por el otro las restantes, para ver que alimentos son esas observaciones he unido la variable order (orden del dendograma) de cluster11.2 con el nombre de los alimentos para poder realizar una correspondencia visual entre los grupos y los nombres de los alimentos así el primer cluster sería buey, chuleta de cerdo, jamón ahumado y cerdo, es un extraño cluster pero continuemos con el estudio para ver porque se produce esta asociación.. ¿Qué ocurriría si tuvieramos una gran cantidad de observaciones y una referencia visual planterara problemas? En ese caso tras identificar el número de cluster emplearíamos una técnica por medios divisorios (Partitioning methods en terminología anglosajona) que situaría cada observación en los alguno de los cluster de forma que se minimizara la suma de las disimilaridades. Esto se hace con R del siguiente modo:
> cluster11.2b<-pam(alimentos.2,2) Available components:
[1] "medoids" "clustering" "objective" "isolation" "clusinfo"
[6] "silinfo" "diss" "call" "data"
|
La función pam permite hacer lo que señalabamos antes, pero en este caso nos encontramos con que los cluster formados son distintos a los que formábamos con los métodos jerárquicos ya que el tamaño de los cluster es distinto que el tamaño anterior, como siempre veámoslo gráficamente que es como mejor se puede ver como trabajan las distintas funciones de R:
> par(mfrow=c(2,2)) |
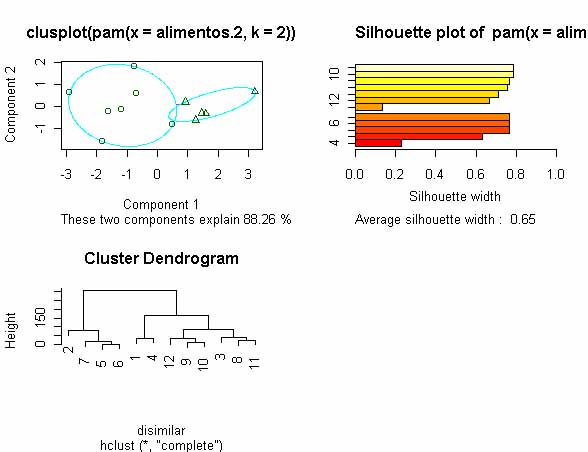
Hemos dicho a R que nos ofrezca los gráficos en una pantalla dividida en 4 celdas con la función par y después graficamos los análisis con plot, vemos que la función pam ofrece 2 gráficos: uno de componentes principales y otro de distancias entre los centroides de los cluster. Vemos que cada método ha establecido distintos grupos, ahora comparemos las dos formas de agrupamiento:
> data.frame(alimentos$Alimentos,cluster11.2$order,cluster11.2b$clustering) |
 |
| Alimento |
Jerárquicos
|
Métodos divisorios
|
| Hamburguesa |
1
|
1
|
| Buey |
2
|
2
|
| Pollo |
1
|
1
|
| Cordero |
1
|
2(*)
|
| Jamón ahumado |
2
|
2
|
| Cerdo |
2
|
2
|
| Chuleta de cerdo |
2
|
2
|
| Pescado azul |
1
|
1
|
| Sardinas |
1
|
1
|
| Atún en lata |
1
|
1
|
| Mejillones en lata |
1
|
1
|
| Mejillones hervidos |
1
|
1
|
El problema lo hemos encontrado con el cordero que se ha unido al cluster 2 y en el análisis jerárquico se había unido al cluster 1. Como siguiente paso en nuestro ejemplo vamos a buscar una regla de funcionamiento para la agrupación de observaciones y esto lo hacemos sumarizando el objeto cluster11.2b que creamos con anterioridad:
> summary(cluster11.2b) Numerical information per cluster: (3)
size max_diss av_diss diameter separation
[1,] 7 77.79389 33.07663 132.2044 35.48239
[2,] 5 80.74652 31.52185 141.0744 35.48239
Isolated clusters:
L-clusters: character(0)
L*-clusters: character(0)
Silhouette plot information: (4)
cluster neighbor sil_width
11 1 2 0.7879602
10 1 2 0.7839538
9 1 2 0.7648888
8 1 2 0.7563286
3 1 2 0.7093818
12 1 2 0.6655977
1 1 2 0.1340588
7 2 1 0.7681916
6 2 1 0.7680220
5 2 1 0.7675267
2 2 1 0.6322059
4 2 1 0.2312497
Average silhouette width per cluster:
[1] 0.6574528 0.6334392
Average silhouette width of total data set:
[1] 0.6474471
Dissimilarities :
[1] 175.524927 132.204387 35.482390 95.010526 95.042096 110.059075
[7] 113.516519 67.891752 77.793894 92.162302 47.549974 307.159568
[13] 141.074448 80.932070 80.746517 65.772335 287.789854 242.163354
[19] 252.293658 266.836448 221.711524 166.105388 226.386837 226.501656
[25] 241.518115 26.343880 65.883913 55.538185 41.367741 85.877820
[31] 60.332413 60.415230 75.432089 147.040811 101.214080 111.287421
[37] 125.868543 80.734132 1.414214 15.165751 207.028983 161.320457
[43] 171.396879 186.136751 140.932608 15.033296 207.159359 161.456774
[49] 171.554335 186.222689 141.039002 222.128341 176.449114 186.549966
[55] 201.233422 156.044865 46.031402 37.473858 23.398504 66.445466
[61] 11.504782 25.729361 20.685502 17.932094 31.293610 45.282337
Metric : euclidean
Number of objects : 12
Available components:
[1] "medoids" "clustering" "objective" "isolation" "clusinfo"
[6] "silinfo" "diss" "call" "data"
|
En (1) tenemos la media de cada variable dentro del cluster, los alimentos "sanos" con menor aporte calórico, menos grasas y más calcio forman el cluster 1 y los "menos sanos" forman el cluster 2. En (2) tenemos el vector que coloca cada observación en un cluster. En (3) tenemos información numérica sobre cada cluster como el tamaño, distancias medias y máximas,... En (4) tenemos como funciona el algoritmo que clasifica las observaciones, le funcionamiento es análogo a la función hclust. Este ha sido el estudio que al final nos ha ofrecido una buena función clasificatoria de alimentos aunque en un principio planteara algunas dudas, de todas formas yo sigo sin entender como ha clasificado a las hamburguesas como un alimento "sano"...
Capítulo
12: Introducción al Análisis de la Varianza.