niels henrik abel

Abel nació el 5 de agosto de 1802 en la Isla de Finnoy (Noruega) y falleció el 16 de abril de 1829 en Noruega.
Este matemático es considerado como uno de los más ilustres genios de las ciencias exactas, a los que aportó gran número de nuevas ideas.
La vida de Abel estuvo dominada por la pobreza.
El profesor de Abel, Holmboe, reconoció su talento para la matemática, debido a su falta de dinero para asistir a una colegiatura, ingresó a la universidad en 1821 y se graduó en 1822.
Publicó en 1823 escritos sobre teoría de funciones, el inicio de la teoría de las ecuaciones integrales y las series. En 1824 dió la primera demostración correcta de la improbabilidad de resolver por radicales la ecuación general de 5º grado.
Una importante clase de funciones trascendentales se denominan (después de su descubrimiento) como las ecuaciones, grupos y cuerpos abelianos. Abel le dio una generalización más amplia al teorema del binomio formulado por
Newton y
Euler, incluyendo los casos de exponentes irracionales e imaginarios.
Ganó un premio del gobierno para viajar al extranjero, donde visitó Alemania y Francia.
Después de su visita a París, regresó a Noruega bastante débil ya que padecía de tuberculosis.
A pesar de su mala salud y la pobreza, continuó con la teoría de las funciones elípticas de mayor importancia en el desarrollo de la teoría total, revolucionando el entendimiento de las funciones elípticas por el estudio de la función inversa de esa función.
BHASKARA
Nació en la India en el año 1114 y murió en el año 1185.
Elaboró una teoría de los números que resultó ser de suma utilidad durante siglos. En 1150 usó la inicial de cuadrado para indicar la segunda potencia, y la inicial de volúmen para la tercera potencia de un número. Hizo uso de las letras como representación de las incógnitas y dio solución a diversas ecuaciones de primer y de segundo grado.
Se le atribuye la recopilación de temas matemáticos conocida como
Lilavati, basada en la obra
Brahmagupta; la obra trata, entre otros temas, de las cuatro operaciones, elevación de una cantidad a la segunda potencia, extracción de raíces cuadradas y cúbicas, proporciones, progresiones, figuras planas y problemas de sombras.
Sus trabajos quedaron recopilados en las obras
Sidhantasiromani y
Karanakutuhala.
Para hallar las raíces de la ecuación de segundo grado: ax2 + bx + c = 0, se utiliza la Fórmula de Bhaskara:
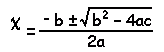
augustin-louis cauchy
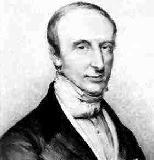
Cauchy fue un matemático francés que nació en París en el año 1789 y falleció en 1857.
Estudió Ingeniería y en 1810 en Cherbourg trabajó como ingeniero militar junto a Napoleón en la invasión a Inglaterra.
En 1813 volvió a París y allí fue persuadido por
Laplace y
Lagrange para convertirse en un devoto de la matemática. Fue profesor en diversas escuelas técnicas, en la Universidad de París y en la de Turín (durante su exilio por razones políticas).
En 1814 publicó la integral definida que llegó a ser la base de la teoría de las funciones complejas. Gracias a Cauchy, el análisis infinitesimal adquiere bases sólidas.
Se lo considera como uno de los fundadores del moderno análisis matemático. Se destacan sus trabajos sobre el análisis y la teoría de permutación de grupos, funciones de variable compleja, convergencia y divergencia de series infinitas, determinantes, probabilidad, física matemática y sus teoremas sobre sistemas de ecuaciones diferenciales.
Numerosos términos matemáticos llevan su nombre: el teorema integral de Cauchy, la teoría de las funciones complejas, las ecuaciones de Cauchy-Riemann y Secuencias de Cauchy.
Cauchy, produjo casi 800 escritos, pero fue desaprobado por la mayoría de sus colegas. De su voluminosa obra cabe citar
Curso de análisis,
Tratado de cálculo diferencial e integral y
Lecciones sobre las aplicaciones del cálculo infinitesimal a la geometría.
En el prefacio de su obra
Analyse Algébrique, de 1822, escribe :
"He tratado de dar a los métodos todo el rigor que se exige en geometría, sin acudir jamás a los argumentos tomados de la generalidad del álgebra. Tales argumentos, aunque bastante admitidos, sobre todo al pasar de las series convergentes a las divergentes, de las cantidades reales a las imaginarias, se me ocurre que no deben ser considerados sino como inducciones, adecuadas a veces para hacer presentir la exactitud y la verdad, pero que no están de acuerdo con la exactitud tan alabada de las ciencias matemáticas. Además, debe señalarse que ellas tienden a atribuir a las fórmulas algebraicas una extensión ilimitada, en tanto que en la realidad, la mayor parte de estas fórmulas sólo subsisten bajo ciertas condiciones y para determinados valores de las cantidades que encierran. Determinando esas condiciones y esos valores, fijando de una manera precisa el sentido de las notaciones que utilizo, toda vaguedad desaparece".
rene descartes
"Consideraría que no sé nada de Física si tan sólo fuese capaz de expresar cómo deben ser las cosas,
pero fuese incapaz de demostrar que no pueden ser de otra manera. No obstante,
habiendo logrado reducir la Física a las Matemáticas, la demostración es entonces posible,
y pienso que puedo realizarla con el reducido alcance de mi conocimiento"
René Descartes
 Este filósofo y matemático francés nació el 31 de marzo de 1596 y falleció en Estocolmo, Suecia el 11 de febrero de 1650.
Este filósofo y matemático francés nació el 31 de marzo de 1596 y falleció en Estocolmo, Suecia el 11 de febrero de 1650.
De familia burguesa, su padre lo envió a un colegio jesuita. Como su salud era precaria y necesitaba dormir más que los demás niños, sus maestros lo dejaban dormir hasta el mediodía.
Cursó estudios normales de lógica, ética, metafísica, historia, ciencias y literatura. Luego se dedicó a trabajar independientemente en álgebra y geometría. Siguió sus estudios en la Universidad de Poitiers, donde cursó las materias de derecho. En cuanto recibió su diploma, abandonó el estudio de las letras y pasó los dos siguientes años estudiando matemáticas.
En 1619, contando con 22 años, prestó servicio voluntario en el ejército del príncipe Mauricio de Nassau y gracias a eso conoció a
Isaac Beeckman, un famoso matemático de Holanda, que se convirtió en su amigo y mentor. Cuatro meses después Descartes le comunicó a su amigo el descubrimiento de una nueva manera de estudiar geometría.
Se propuso corregir los métodos de los geómetras griegos mediante el manejo de líneas y figuras tridimensionales en una gráfica. Dibujaba un gráfico marcando unidades en una línea horizontal (eje x) y una línea vertical (eje y); de este modo, cualquier punto del gráfico podía describirse con dos números. El primer número representaba una distancia en el eje x y el otro número representaba una distancia en el eje y; llamadas luego coordenadas cartesianas (en honor a él ya que su nombre en latín era Cartesius). Aunque conservaba las reglas de la geometría euclidiana, combinaba el álgebra y la geometría, consideradas entonces como independientes, para formar una nueva disciplina matemática llamada geometría analítica.
En 1626 se estableció en París donde se dedicó a la construcción de elementos ópticos hasta 1629, cuando influenciado por el Cardenal de Berulle viaja a Holanda y escribe para el periódico Le Monde una teoría física del universo, pero sabiendo los problemas de Galileo con la Inquisición, decide abandonar la idea y esta teoría se publica luego de su muerte.
Entre 1629 y 1649 vivió en Holanda, allí estudió además de filosofía y matemática, óptica, física, química, anatomía y medicina.
La frase "Cogito ego sum" ("Pienso, existo", mal traducida por "Pienso, luego existo") fue la frase que definió su óptica filosófica.
El 8 de Junio de 1637 Descartes publicó su geometría analítica como un apéndice de su obra Discurso del método. También definió la recta tangente como una posición límite de la recta secante. En su libro, Geometríe, expone un análisis del álgebra general y es allí donde por primera vez denota con las primeras letras del alfabeto aquellas cantidades conocidas, y con las últimas las cantidades desconocidas, notación que ha prevalecido hasta la actualidad.
En 1644, publica Principia Philosophiae, dedicado esencialmente a la física, en especial a las leyes de movimiento.
En 1647 recibió una pensión de la corte francesa en honor a sus descubrimientos, y en 1649 viajó a Suecia, por invitación de la Reina Cristina, quien quería que le enseñara filosofía. Descartes debía hacerlo a las cinco de la mañana en una habitación muy húmeda y fría y debido a su precaria salud enfermó de pulmonía y falleció cinco meses después.
eratostenes

Este astrónomo, geógrafo, matemático y filósofo griego nació en la ciudad de Cirene aproximadamente en el año 276 A.C. y falleció alrededor del año 194 A.C.
Vivió en Atenas hasta que fue llamado a Alejandría (245 A.C.) para educar a los hijos de Tolomeo III y para dirigir la biblioteca de la ciudad.
Fue el primero en establecer la longitud de la circunferencia de la Tierra (252.000
estadios: casi 40 millones de metros) con un error de unos 90 kilómetros respecto a las estimaciones actuales. Para esto, utilizó las siguientes observaciones experimentales: en las ciudades de Alejandría y Siena, situadas en un mismo meridiano dos objetos similares no proyectaban la misma sombra al ser iluminados por el Sol en idéntico momento, debido a que la curvatura de la Tierra hace que esta sombra sea mayor cuanto más alejado está el objeto del ecuador.
Como Eratóstenes conocía la distancia que separaba a las dos ciudades, a partir de la proporción existente entre las dos sombras pudo determinar con una notable precisión, mediante cálculos trigonométricos, el valor del radio terrestre.
También calculó la oblicuidad de la eclíptica por medio de la observación de las diferencias existentes entre las altitudes del Sol durante los
solsticios de verano e invierno. Un cráter de la Luna lleva su nombre.
Dotado de excepcional sabiduría, fue el primer hombre de ciencia que midió un arco de meridiano, y el inventor del calendario juliano.
Ideó un método para reconocer si un número es primo, conocido como
criba de Eratóstenes.
euclides
Vivió entre 330 A.C. y 275 A.C. en Alejandría; actualmente Egipto.
Reunió y ordenó todos los conocimientos de Geometría estudiados hasta entonces en una serie de trece libros que tituló
"Elementos".
En estos libros el método deductivo, está distinguido entre principios (definiciones, axiomas y postulados) y teoremas que se demuestran a partir de los principios.
En este tratado, es tal la claridad del razonamiento, lo comprensible de las demostraciones y la exactitud del ordenamiento, que durante varios siglos se lo consideró el mejor texto para la enseñanza de la Geometría en las escuelas.
El llamado
algoritmo de Euclides es un método para hallar el MCD (Máximo Común Divisor) de dos números enteros o de dos polinomios. Consiste en dividir el mayor número por el menor, y éste por el resto de dicha división, siguiendo este proceso hasta hallar un cociente exacto. El último divisor es el número buscado.
Los cinco postulados básicos de la geometría euclídea son:
Por dos puntos cualesquiera puede trazarse siempre una, y sólo una, recta que los une.
Toda recta finita puede prolongarse indefinidamente.
Cualquier punto puede ser centro de un círculo de radio arbitrario.
Todos los ángulos rectos son iguales entre sí.
Dada una recta cualquiera y un punto exterior a la misma, existe una, y solamente una, recta paralela a la primera que pasa por el mencionado punto (postulado de las paralelas).
LEONHARD eULER

Leonhard Euler nació en Basilea (ciudad suiza situada a orillas del Río Rin) en el año 1707 y murió en San Petersburgo en 1783.
Fue profesor de Física en la Academia Rusa de Ciencias y de Matemáticas en Berlín.
Científico muy prolífico, tanto en el campo de la física y la astronomía como en el campo de la matemática.
Sus contribuciones más importantes las llevó a cabo en la Teoría de Números y, sobre todo, en el Análisis Matemático; ya que investigó la convergencia de las series algebraicas, reformuló la trigonometría esférica e introdujo diversos símbolos matemáticos (como el número e, la unidad imaginaria i y el sumatorio). Escribió más de 800 tratados, entre los que cabe mencionar
Introducción al análisis de los infinitésimos (1748) e
Instituciones del cálculo diferencial (1755).
pierre fermat

Pierre Fermat nació en Francia en el año 1601 y falleció en 1665.
Estudió abogacía, pero se dedicó por afición a la matemática, materia en la que alcanzó tales conocimientos que le valieron el sobrenombre de "Príncipe de los aficionados".
En 1636 propuso un sistema de geometría analítica similar a uno de
Descartes quien lo propuso unos años después. Reconstruyó la obra de Apolonio aplicando los métodos de la geometría analítica y las notaciones de
Viete y realizó notables descubrimientos en el campo de la teoría de números. Introdujo un método para la determinación de máximos y mínimos de funciones algebraicas.
El último teorema de Fermat (conocido como "gran teorema"), expone que, si n es un número entero mayor que 2, la ecuación x
n + y
n = z
n no tiene solución entera positiva distinta de x = y = z = 0.
Fermat dijo haber descubierto una prueba, pero que no había en la página suficiente margen para darla. Numerosos matemáticos han intentado, sin éxito probar este teorema que figura en el texto
Varia Opera Mathematical (1679), publicado luego de la muerte de Fermat.
Otro de sus teoremas, llamado el "pequeño teorema" enuncia que, dado un número entero cualquiera n no divisible por r, siempre será divisible por r el número n
r-1 - 1.
Fermat tuvo la primera idea sobre el cálculo diferencial y con
Pascal inventó el cálculo de probabilidades.
En óptica geométrica formuló el Principio de Fermat, que dice: "Para ir de un punto a otro, la luz sigue la trayectoria de mínima duración".
carl friedrich gauss

Carl Gauss nació en Alemania en el año 1777 y falleció en 1855.
Se dedicó a la matemática, física y astronomía.
Fue profesor en el observatorio de la Universidad de Gotinga.
Además de contribuir con importantes trabajos al desarrollo de la mecánica celeste y del electromagnetismo, en el campo de la matemática fue un precursor de la geometría no euclídea, inició el estudio de las funciones analíticas y de la topología, sentó las bases de la teoría de los números algebraicos y enunció el teorema fundamental de la aritmética y el del álgebra.
Formuló el siguiente teorema:
El flujo del campo eléctrico creado por un sistema de cargas a través de una superficie cerrada es igual a la suma algebraica de las cargas puntuales interiores a dicha superficie, dividida por la constante dieléctrica del medio. En dicho teorema, conocido como Teorema de Gauss, fue encontrada la defensa contra las minas magnéticas durante la Segunda Guerra Mundial.
La ley de Estadística Gauss es una ley de probabilidad según la cual cuando sobre una magnitud actúan una serie de pequeñas variaciones independientes entre sí, los resultados se disponen alrededor de la media y se distribuyen simétricamente a su alrededor, distribución cuya representación gráfica es la curva de Gauss, en forma de campana.
A cualquier número complejo cuyas partes real e imaginaria son números enteros se lo llama "Entero de Gauss".
Entre sus obras destacan
Teoría del movimiento de los cuerpos celestes,
Investigaciones dióptricas e
Investigaciones sobre el significado de la geodesia superior.
joseph-louis lagrange

Lagrange nació en Francia el 25 de enero del año 1736 y falleció el 10 de abril de 1813.
Siendo un niño llegó a sus manos una memoria de
Halley y allí descubrió la magia de la matemática.
A los dieciséis años de edad, fue nombrado profesor de matemáticas en la Escuela Real de Artillería de Turín. Luego condujo a un grupo de jóvenes científicos, que fueron los primeros miembros de la Academia de Turín.
Lagrange transcribió a la matemática todos los pequeños temas sobre investigaciones físicas que le traían sus amigos.
A los diecinueve años, resolvió el llamado "problema isoperimétrico", que había desconcertado a los matemáticos durante medio siglo. Le comunicó su demostración a
Euler en una carta, el cual se interesó por la solución, ya que concordaba con un resultado que él mismo había hallado. Euler le respondió a Lagrange, ocultando su propio resultado, para que todo el honor recayera sobre él.
Lagrange inventó un nuevo método de cálculo de variaciones. Este cálculo pertenece a la historia del mínimo esfuerzo, que comenzó en los espejos reflectores de Herón y continuó cuando
Descartes estudió la forma de sus lentes ovales. Lagrange pudo demostrar que los postulados newtonianos de materia y movimiento se adaptaban al amplio principio de economía de la naturaleza. Este principio ha conducido a los resultados de
Hamilton y Maxwell, continúa en la obra de
Einstein y en las últimas fases de la mecánica ondulatoria.
Debido al exceso de trabajo, estaba por temporadas gravemente enfermo. El rey Federico de Alemania lo reprendió diciéndole que el exceso de estudio, desquiciaría su mente. A partir de ese momento Lagrange cambió su actitud hacia el estudio.
Se le deben importantes investigaciones sobre cálculo de probabilidades, mecánica y astronomía.
Llevó a cabo trabajos sobre la teoría de números y la teoría de ecuaciones, en los que planteó la resolución de las ecuaciones diferenciales de derivadas parciales.
Sus principales aportaciones a la física las realizó en el campo de la mecánica racional: estudió el problema de los tres cuerpos, introdujo el principio de las velocidades virtuales y estableció un sistema de ecuaciones del movimiento.
Entre sus obras cabe citar
Miscellanea Taurinensia,
Mecánica analítica (1788) y
Teoría de las funciones analíticas.
pierre-simon laplace
"Nacido para profundizar y perfeccionarlo todo (...)
hubiera acabado con la ciencia del cielo si
esta ciencia pudiera ser acabada"
Jean Baptiste Fourier
 Laplace nació el 28 de marzo de 1749 en Beaumont-en-Auge, Francia y falleció el 5 de marzo de 1827 en París.
Laplace nació el 28 de marzo de 1749 en Beaumont-en-Auge, Francia y falleció el 5 de marzo de 1827 en París.
A los dieciocho años, Laplace ya se había convertido en maestro y matemático en la Escuela Militar de Beaumont.
Consiguió cartas de recomendación y, en 1767, partió hacia París a solicitar la ayuda del francés
D'Alembert. Como no tuvieron éxito las cartas de recomendación; escribió una disertación sobre los principios de la mecánica y se la envió con la solicitud de que le concediera una audiencia. D’Alembert quedó tan impresionado con el talento de Laplace, que lo mandó llamar enseguida.
Con la ayuda de D’Alembert, obtuvo el nombramiento de profesor de matemáticas en la Escuela Militar de París.
El primer trabajo científico de Laplace fue su aplicación de las matemáticas a la mecánica celeste. Ideó una teoría, que confirmó con pruebas matemáticas, donde expresaba que las desviaciones de los planetas de sus órbitas eran normales y se corregían solas en el transcurso de largas etapas de tiempo. Está teoría ha soportado la prueba del tiempo sin sufrir más que algunas pequeñas correcciones.
En los años siguientes fue aclarando los conocimientos científicos sobre las fuerzas elementales de la Naturaleza y el Universo. Escribió artículos acerca de la fuerza de gravedad, el movimiento de los proyectiles y el flujo y reflujo de las mareas, la precesión de los equinoccios, la forma y rotación de los anillos de Saturno y otros fenómenos.
Al estudiar la atracción gravitacional de un esferoide sobre un objeto externo, ideó lo que se conoce hoy como ecuación de Laplace, que se usa para calcular el potencial de una magnitud física en un momento dado mientras está en movimiento continuo. Esta ecuación no sólo tiene aplicación en la gravitación, sino también en la electricidad, la hidrodinámica y otros aspectos de la física.
En 1789 es nombrado miembro de la Comisión de Pesos y Medidas que establecerá el sistema métrico utilizado en la actualidad llegando a ser presidente de esta comisión; y en 1792 participa en la organización de la Escuela Politécnica.
Napoleón lo designa ministro del Interior. Es miembro del Senado desde 1799 y llega a ser su vicepresidente en 1803. Una vez constituido el Imperio Napoleón lo nombra Conde en 1806.
Entre 1799 y 1825, Laplace reunió sus escritos en una obra de cinco volúmenes Mecánica Celeste, en la que contaba la historia de la astronomía y ofrecía una solución completa a los problemas mecánicos del sistema solar. Más tarde publicó un volumen titulado El sistema del mundo.
Las contribuciones matemáticas de Laplace son de primera importancia. Destacan sus investigaciones sobre el cálculo de probabilidades. Su Teoría analítica de las probabilidades (1812) representa la introducción de los recursos del análisis en el estudio de los fenómenos aleatorios. Las numerosas aplicaciones que hizo de este cálculo dieron origen al cálculo de diferencias finitas parciales, a su método para la reducción de ciertas integrales como series, a la teoría de las funciones generatrices, el principio de los
mínimos cuadrados, la solución al problema "de la aguja" propuesto por
Buffon en 1777 para obtener una aproximación del número pi y el conocido posteriormente como
Teorema de Bayes.
En los últimos años de su vida se dedicó a apoyar a jóvenes científicos
(Chaptal, Dulong, Gay-Lussac, Biot, Poissson,... ) mediante la Sociedad de Arcueil, fundada por él y su colega Berthollet para ayudar a los nuevos investigadores. Esta sociedad publica tres volúmenes de memorias con importantes trabajos de matemática y física.
En vida aún, fue elegido para ser uno de los Cuarenta Inmortales de la Academia Francesa.
En la actualidad el estado francés ha bautizado con su nombre una de las instituciones científicas más importantes del país: el Instituto Pierre Simon de Laplace.
Gottfried Wilhelm leibniz

Leibniz nació en la ciudad de Leipzig (Alemania) en el año 1646.
Este filósofo y matemático se educó leyendo la biblioteca paterna y a los 12 años hablaba latín, entendía el griego y estudiaba lógica aristotélica.
En 1661 entró en la Universidad de Leipzig, en la que se doctoró en 1663 con la tesis
Disputatio metaphysica de principio individui. Durante un año estudió en Jena matemática, historia y jurisprudencia.
A fines de 1664 se convirtió en maestro de filosofía. En 1666 publicó
De arte combinatoria.
Alrededor del año 1668 se interesó por la política, y llegó a considerar como objetivos prioritarios la unificación de las Iglesias y la creación de una sociedad de las artes y de las ciencias.
En 1672 fue enviado por el elector de Maguncia a París, donde conoció a
Arnauld y a Huygens, quien le inició en la matemática moderna. Escribe sus obras
Teoría del movimiento abstracto y
Teoría del movimiento concreto. En 1676, poco después de haber descubierto el cálculo diferencial, inventó el cálculo infinitesimal.
Leibniz argumentando que el signo de multiplicación x podía confundirse con una equis, lo simplificó, reduciéndolo a un punto; años más tarde hizo lo mismo con el signo de división usando los dos puntos.
En 1712 su fama impulsó al zar Pedro el Grande a llamarle como consejero. Fue nombrado barón en 1714, año en que escribió la Monadología, síntesis última de su filosofía, pero cuya importancia no fue comprendida en su tiempo.
Leibniz falleció en Hannover en 1716.
John neper o napier

Nació en
Escocia en 1550 y falleció en 1617.
Abandonó los estudios de teología para dedicarse a materias científicas, en particular, mecánica, balística, astronomía y problemas de guerra. Buscando un método de simplificación de los cálculos numéricos ideó los
logaritmos neperianos por comparación entre progresiones, que anunció en 1614 en su libro
Mirifici logarithmorum canonis descriptio y en
Mirifici logarithmorum canonis constructio (1619).
A Napier se le debe el descubrimiento del número e, y a
Euler el haberlo hecho popular. Fue Euler el primero en señalarlo con la letra e y calcularlo hasta el 13
a cifra decimal:
e = 2,7182818284590 También se dedicó al cálculo sistemático de las tablas de los logaritmos.
De sus obras reviste mayor importancia Rabdologiae seu numerationis per virgulas libri duo (1617), donde se formulan los métodos para realizar mediante varillas cifradas, llamadas regletas de Neper, la multiplicación, la división y la extracción de raíces cuadradas y cúbicas.
Además sentó los principios sobre los que se basaron posteriormente ciertas máquinas de calcular.
Napier también contribuyó en el campo de la trigonometría esférica con las relaciones entre los elementos de los triángulos esféricos y llanos que se conocen como el teorema de Neper y las fórmulas de Neper.
blaise pascal

Nació en Clermont-Ferrand (Francia) en el año 1623 y murió en París en 1662.
Hijo de una familia de la alta burguesía, su padre se instaló en París en 1631 y lo introdujo en la sociedad científica y literaria de la Académie de Mersenne, despertando su precoz vocación.
A los 14 años dominaba las matemáticas; a los 16 escribió un ensayo sobre las secciones cónicas que asombró a
Descartes, y a los 18 inventó la prensa hidráulica, imaginó el triángulo aritmético y creó el cálculo de probabilidades. En 1642, para ayudar a su padre en un trabajo fiscal, ideó una máquina calculadora que perfeccionó 10 años después.
Entre otros valiosos aportes a la ciencia, se le deben las leyes de la pesantez del aire y del equilibrio de los líquidos; principio que lleva su nombre. Hasta 1654, se concentró básicamente en problemas físico-matemáticos; el tema de sus trabajos científicos fue sobre todo la estática de los fluidos, e intentó establecer por vía experimental la crítica a la tesis del horror de la naturaleza al vacío.
Tras la muerte de su padre (1651) y el ingreso de su hermana Jacqueline en un convento (1652) Blaise Pascal se avocó a la escritura y figura entre los primeros prosistas franceses. Sus obras más importantes son:
Las Provinciales, conjunto de 18 cartas (1656-1657) en defensa de Arnauld, y en las que ataca a la Sorbona y a los jesuitas, y sus
Pensamientos, fragmentos de una apología del cristianismo, publicados después de su muerte.
Para Pascal, la fe es intuitiva; una decisión tomada libremente desde la ignorancia sobre la existencia y la voluntad de Dios.
pitagoras

Nació en Samos (Grecia) en el 570 A.C. y murió en Metaponte (Grecia) en el 480 A.C. Fue filósofo y matemático.
Thales de Mileto, que ya era anciano, le enseñó algunos conocimientos y le aconsejó que visitara Egipto para ponerse en contacto con las fuentes mismas de la Geometría.
Desterrado por el tirano Polícrates, marchó a Crotona (530 A.C.), donde fundó una escuela científica, filosófica, política y religiosa especialmente interesada en matemáticas, astronomía, fisiología y medicina.
Todas las doctrinas de su escuela giraban alrededor de un principio fundamental: "Los números son el principio de las cosas".
Según los pitagóricos una ciencia exacta sólo puede obtenerse por medio de los números y el universo es imperfecto porque las cosas no son la realidad de los números sino su imitación.
Limitado a los números enteros, el pitagorismo estudió la media aritmética, la geométrica y la armónica, además de investigar relaciones numéricas, tales como los números perfectos (número que es igual a la suma de todos sus divisores).
Pitágoras demostró una relación fundamental que vincula los lados de un triángulo rectángulo. Esta demostración se conoce como el Teorema de Pitágoras:
En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Si a es la hipotenusa y b y c los catetos, la expresión algebraica viene dada por: a2 = b 2 + c2.
tartaglia

Su verdadero nombre era Niccolò Fontana. Nació en Brescia (Italia) en 1499 y murió en Venecia (Italia) en el año 1557.
Recibió el sobrenombre de Tartaglia (tartamudo) por un defecto en el habla a consecuencia de una herida durante el saqueo de su ciudad natal por las tropas de Gastón de Foix, en 1512.
Fue el primero en aplicar la matemática a la artillería y al arte militar.
Escribió:
Tratado general de números y medidas (1556-1560), que dejó inconcluso y se publicó después de su muerte.
También fue el primero en resolver la ecuación de tercer grado e ideó el triángulo que permite obtener los coeficientes del desarrollo binomial (conocido como el triángulo de Tartaglia). Este triángulo es una tabla triangular en la que se disponen números enteros en líneas horizontales, de modo que los números de la
línea enésima son los coeficientes numéricos del desarrollo (n-1)-ésimo de un binomio. Para la construcción del triángulo de Tartaglia debe tenerse en cuenta:
a) el vértice es la unidad;
b) cada una de las líneas tiene un término más que la anterior;
c) cada línea empieza y termina con la unidad;
d) un término cualquiera es igual a la suma de los dos de la línea anterior entre los que está situado:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
..............................
Según este triángulo, el desarrollo de la cuarta potencia del binomio (x + a) será:
(x + a)4 = x4 + 4x3a + 6x2a2 + 4xa3 + a4, y la quinta potencia:
(x + a)5 = x5 + 5x4a + 10x3a2 + 10x2a3 + 5xa4 + a5.
thales de mileto

Nació en Mileto (Grecia) en el año 640 AC. y murió casi centenario (edad de excepción en aquella época en que el promedio de vida era de unos treinta años) en el año 546 AC.
Fue uno de los siete sabios de Grecia. Se lo considera uno de los precursores de la física, la geometría y la astronomía. Además es el primer filósofo de nombre conocido de la tradición occidental.
Afirmó que todas las cosas son en su esencia agua, que constituye el principio del que derivan por sucesivas condensaciones y evaporaciones. Esta afirmación tiene un aspecto científico innovador: el intento de encontrar una explicación de la realidad atendiendo únicamente a los datos que aporta la propia realidad, y también un aspecto que la hace depender del mundo cultural de su época: la identificación de las cosas con el principio de éstas.
Tuvo fama como astrónomo al predecir un eclipse de Sol, que fue visible en Asia Menor.
Hizo varios viajes a Egipto durante la primera mitad de su vida y recibió de los sacerdotes egipcios todos los conocimientos matemáticos que después enseñaba en Mileto. Descubrió numerosas propiedades de ángulos, triángulos y segmentos proporcionales. Formulando el siguiente teorema:
Si tres o más paralelas son intersecadas por dos transversales, dos segmentos de una de las transversales y los correspondientes de la otra, forman proporción.
Esto equivale a decir que la proyección paralela de una recta sobre otra conserva la proporcionalidad de los segmentos. Si a1, a2, a3, ..., an y b1, b2, b3, ..., bn son los segmentos que las rectas paralelas r0, r1, r2, r3,..., rn, rn+1 determinan respectivamente sobre dos rectas a y b, el teorema se expresa por las igualdades: a1/b1 = a2/b2 = a3/b3 = ... = an/bn.
alfred north whitehead
Matemático y filósofo inglés, nacido en Kent en 1861. Presidió una cátedra de matemática en Londres y, a partir de 1924, una de filosofía en Estados Unidos.
Junto con Bertrand Russell publicó la obra en tres tomos
Principia Mathematica, donde se investiga la estructura lógica de las matemáticas y del pensamiento racional.
Estudió la lógica simbólica y formuló una filosofía orgánica que investiga las bases de las matemáticas, las ciencias sociales y naturales, la estética, la ética y la religión, de manera de englobar los conocimientos en una misma concepción del universo.
Sus pensamientos individualistas, de profundas raíces morales, se reflejan en sus obras:
- Science and the Modern World (1925).
- Process and Reality (1929).
- Adventures of Ideas (1933).
Whitehead murió en 1947.

 Abel nació el 5 de agosto de 1802 en la Isla de Finnoy (Noruega) y falleció el 16 de abril de 1829 en Noruega.
Abel nació el 5 de agosto de 1802 en la Isla de Finnoy (Noruega) y falleció el 16 de abril de 1829 en Noruega. 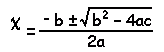
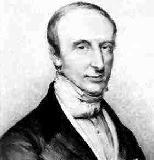 Cauchy fue un matemático francés que nació en París en el año 1789 y falleció en 1857.
Cauchy fue un matemático francés que nació en París en el año 1789 y falleció en 1857.  Este filósofo y matemático francés nació el 31 de marzo de 1596 y falleció en Estocolmo, Suecia el 11 de febrero de 1650.
Este filósofo y matemático francés nació el 31 de marzo de 1596 y falleció en Estocolmo, Suecia el 11 de febrero de 1650.  Este astrónomo, geógrafo, matemático y filósofo griego nació en la ciudad de Cirene aproximadamente en el año 276 A.C. y falleció alrededor del año 194 A.C.
Este astrónomo, geógrafo, matemático y filósofo griego nació en la ciudad de Cirene aproximadamente en el año 276 A.C. y falleció alrededor del año 194 A.C.  Leonhard Euler nació en Basilea (ciudad suiza situada a orillas del Río Rin) en el año 1707 y murió en San Petersburgo en 1783.
Leonhard Euler nació en Basilea (ciudad suiza situada a orillas del Río Rin) en el año 1707 y murió en San Petersburgo en 1783. Pierre Fermat nació en Francia en el año 1601 y falleció en 1665.
Pierre Fermat nació en Francia en el año 1601 y falleció en 1665.  Carl Gauss nació en Alemania en el año 1777 y falleció en 1855.
Carl Gauss nació en Alemania en el año 1777 y falleció en 1855.  Lagrange nació en Francia el 25 de enero del año 1736 y falleció el 10 de abril de 1813.
Lagrange nació en Francia el 25 de enero del año 1736 y falleció el 10 de abril de 1813.  Laplace nació el 28 de marzo de 1749 en Beaumont-en-Auge, Francia y falleció el 5 de marzo de 1827 en París.
Laplace nació el 28 de marzo de 1749 en Beaumont-en-Auge, Francia y falleció el 5 de marzo de 1827 en París.  Leibniz nació en la ciudad de Leipzig (Alemania) en el año 1646.
Leibniz nació en la ciudad de Leipzig (Alemania) en el año 1646.  Nació en
Escocia en 1550 y falleció en 1617.
Nació en
Escocia en 1550 y falleció en 1617.  Nació en Clermont-Ferrand (Francia) en el año 1623 y murió en París en 1662.
Nació en Clermont-Ferrand (Francia) en el año 1623 y murió en París en 1662.  Nació en Samos (Grecia) en el 570 A.C. y murió en Metaponte (Grecia) en el 480 A.C. Fue filósofo y matemático.
Nació en Samos (Grecia) en el 570 A.C. y murió en Metaponte (Grecia) en el 480 A.C. Fue filósofo y matemático. Su verdadero nombre era Niccolò Fontana. Nació en Brescia (Italia) en 1499 y murió en Venecia (Italia) en el año 1557.
Su verdadero nombre era Niccolò Fontana. Nació en Brescia (Italia) en 1499 y murió en Venecia (Italia) en el año 1557. Nació en Mileto (Grecia) en el año 640 AC. y murió casi centenario (edad de excepción en aquella época en que el promedio de vida era de unos treinta años) en el año 546 AC.
Nació en Mileto (Grecia) en el año 640 AC. y murió casi centenario (edad de excepción en aquella época en que el promedio de vida era de unos treinta años) en el año 546 AC.