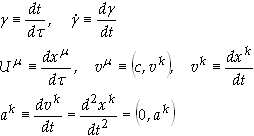
Coordinate Acceleration

Back to Physics World
Back to General Relativity

In this page an expression is derived expressing the coordinate acceleration a^k = dv^k/dt in terms of the Christoffel symbols and coordinate velocities v^k = dx^k/dt.  Solving for a^k gives the final result for the coordinate acceleration [1]. Consider the spacetime event X defined as follows:

X = (ct, x, y, z) = (ct, r) = (x⁰, x¹, x², x³)

In what follows the following terms will be used

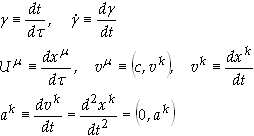
The 4-velocity can be represented in terms of the coordinate velocity as

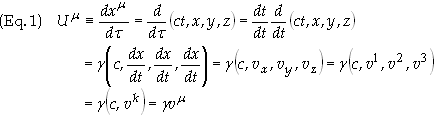
Take the derivative of Eq. (1) with respect to proper time t to obtain

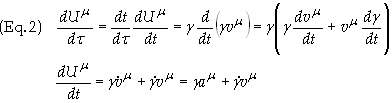
Eq. (2) can be written in terms of components as

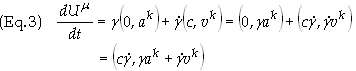
The geodesic equation can be expressed in terms of the coordinate velocity

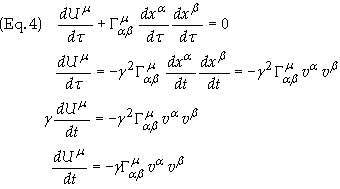
G^m_ab are the Christoffel Symbols (of the second kind) and are defined as

Substitute Eq. (3) into the geodesic equation Eq. (4), noting that

gives

Equating components in Eq. (7) gives

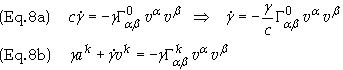
Substitute Eq. (8a) into Eq. (8b) and cancel g to give

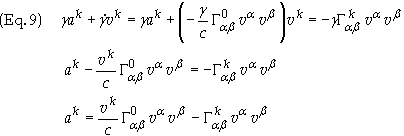
 Eq. (9) is the result we are looking for, i.e. a^k is the expression for the coordinate acceleration. It is noted that the result arrived at in Eq. (9) is identical to the result as obtained by Mould [1]

Application to a Schwarzschild Field

In this section we will use Eq. (10) to determine the coordinate acceleration for a particle in free-fall in a Schwarzschild gravitational field. We will assume that the particle is falling radially towards the center of the source. The metric for such a field is given by

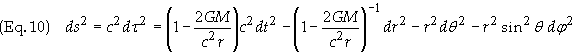
In order to simplify the equations that follow define

The nonvanishing components of the metric tensor are

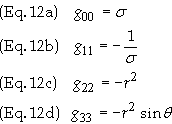
The components of the metric form a diagonal matrix. The components of the inverse matrix is also diagonal and are given by

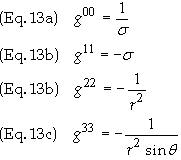
Since the particle is falling radially, v_q = v_f = 0 , it follows that v^m =  (v⁰, v¹, v², v³) =  (c, v_r, v_q, v_f) = (c, v_r, 0, 0). The radial acceleration is thus given by

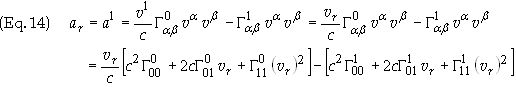
We now seek to find the Christoffel symbols used in Eq. (14). We start by noting that for the metric in Eq. (12) the Christoffel symbols in Eq. (14) are defined as

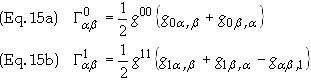
Find the non-vanishing Christoffel symbols:

G⁰₀₀: Use Eq. (15a) with a = b = 0 we obtain

G⁰₀₁: Use Eq. (15a) with a = 0, b = 1 we obtain

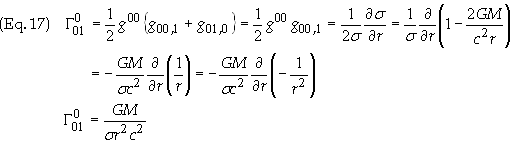
G⁰₁₁: Use Eq. (15a) with a = 1, b = 1 we obtain

G¹₀₀: Use Eq. (15b) with a = b = 0 we obtain

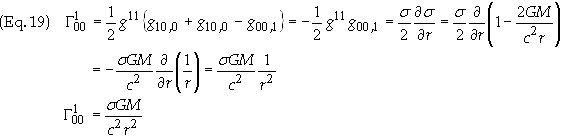
G¹₀₁: Use Eq. (15b) with a =0, b = 1 we obtain

G¹₁₁: Use Eq. (15b) with a = b = 1 we obtain

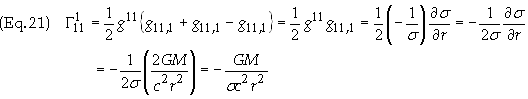
Summary of non-vanishing Christoffel symbols used in Eq. (14)

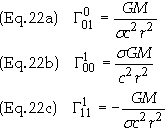
When the Christoffel symbols in Eq. (22) and that v^m = (c, v_r, 0, 0) are substituted into Eq. (14) we obtain

which reduces to

Substitute Eq. (22) into (23) to obtain

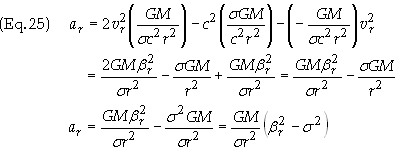
Mould’s result is [2]

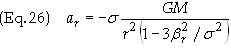
References:

[1] Basic Relativity, Richard A. Mould, Springer Verlag, (1994), p. 217, Eq. (7.57).
[2] Ref. 1, p. 329, Eq. (12.37)

Back to General Relativity
Back to Physics World