A statistical analysis of the gaps between prime numbers has shown an exciting result. The correlations between neighbouring primes have been studied extensively (see Jumping champions and links from Andrew Granville's page, for example). We report here some further correlations, and a heuristic explanation (see also Correlations in Prime Number Distribution and L-function Zeros). The distribution for the differences of the prime numbers is shown in the figure below for the fiftieth million set of primes.

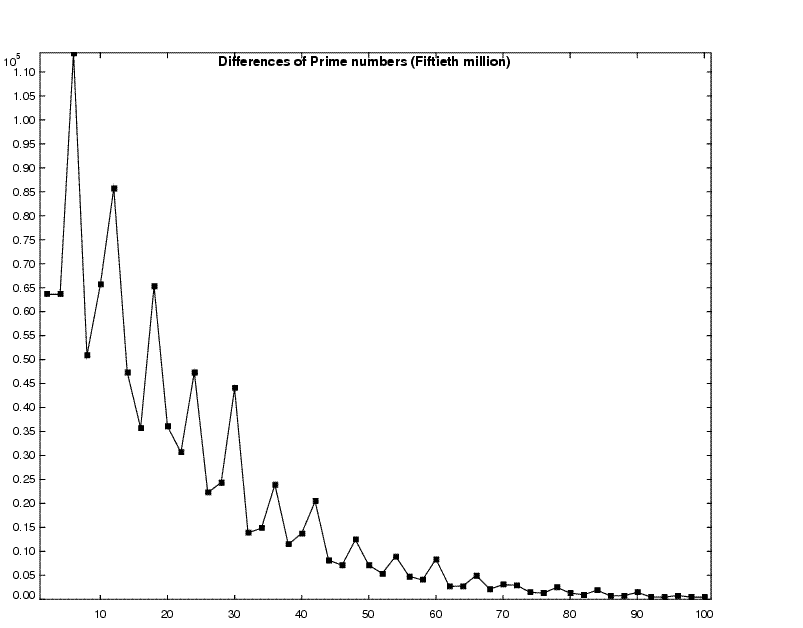
The horizontal axis shows the gap between consecutive primes, and the vertical axis shows the count for the number of times the difference occurs in the fiftieth million set of primes. The structure in the histogram is interesting, e.g., the peaks when the differences are multiples of 6. When a prime number is divided by 6, the remainder is either 1 or 5. An analysis of the peaks has shown evidence for a correlation between the probability of the remainder being 1 or 5 and the remainder for the previous prime number. The table below shows the correlation when the fiftieth million set of zeros is analysed. The first row shows the probabilities for a prime number with remainder 1 being followed by a prime number with remainder 1 or remainder 5 respectively. The second row shows the probabilities for a prime number with remainder 5 being followed by a prime number with remainder 1 or remainder 5 respectively. The dependence on the previous prime number is clear from the differences in the table entries. We see that the ratio of the number of neighbouring primes with the same remainder to the number of neighbouring primes with different remainders is 0.811.

Fiftieth million primes, Divisor 6
Remainder	1	5
1	0.224	0.276
5	0.276	0.224

One can give a heuristic argument for the correlation. All primes will be of the type 6*k+1 or 6*k+5. These two arithmetic progressions are interlaced. We know that the density of primes at N is of order 1/ln(N). Let us consider a heuristic model, i.e., each term in either of the arithmetic progressions has a "probability" 3/ln(N) of being prime. The heuristic model predicts that the the ratio of the number of neighbouring prime pairs with the same remainders to the number of neighbouring prime pairs with different remainders is (1-3/ln(N)), which numerically is 0.85, almost the observed value. While the heuristic model is quite interesting, it is not a rigorous proof for the correlation. Further, it cannot be the complete story, since it predicts that a gap of 6 will be the most likely gap, while the work on jumping champions (an integer D is called a jumping champion if D is the most frequently occurring difference between consecutive primes <= x for some x ) shows that for very large numbers the most likely gap will be a primorial larger than 6. Thus, the correlation reported here and the heuristic explanation point to areas that ought to be investigated further.

We can also see the effect when we consider the remainder when a prime number is divided by 4. The remainder can be 1 or 3. The table below again shows the correlation when the fiftieth million set of zeros is analysed. The first row shows the probabilities for a prime number with remainder 1 being followed by a prime number with remainder 1 or remainder 3 respectively. The second row shows the probabilities for a prime number with remainder 3 being followed by a prime number with remainder 1 or remainder 3 respectively. The dependence on the previous prime number is clear from the differences in the table entries.

Fiftieth million primes, Divisor 4
Remainder	1	3
1	0.226	0.274
3	0.274	0.226

Shown below are the tables from a similar analysis of the tenth million primes.

Tenth million primes, Divisor 6
Remainder	1	5
1	0.222	0.278
5	0.278	0.222

Tenth million primes, Divisor 4
Remainder	1	3
1	0.224	0.276
3	0.276	0.224

Here is a link giving interesting information about prime numbers. The distribution of zeros of the Riemann zeta function are related to the distribution of primes. Here is a link to some work on the zeros of the Riemann zeta function. Here are links to: my home page, and O. Shanker publication list.