ed e. Molto problematico è invece il caso di quando le operazioni radice e logaritmo non hanno come soluzione un numero reale. Classicamente si studia il caso dell' operazione radice e si deduce poi come si risolve i logaritmi che non hanno soluzione reale. Quando facciamo una radice di esponente pari di un numero negativo, il nostro risultato non può essere un numero positivo, né negativo e non è neanche 0. Allora poniamo per definizione che
ed e. Molto problematico è invece il caso di quando le operazioni radice e logaritmo non hanno come soluzione un numero reale. Classicamente si studia il caso dell' operazione radice e si deduce poi come si risolve i logaritmi che non hanno soluzione reale. Quando facciamo una radice di esponente pari di un numero negativo, il nostro risultato non può essere un numero positivo, né negativo e non è neanche 0. Allora poniamo per definizione che  -1 è l' unità immaginaria che non possiamo scrivere in forma decimale, nemmeno con un' approssimazione, per il motivo appena citato. Siccome si tratta di una costante, possiamo indicarla con un simbolo. Si usa per questo la lettera i. Dal seguente esempio capirete perché si chiama unità immaginaria.
-1 è l' unità immaginaria che non possiamo scrivere in forma decimale, nemmeno con un' approssimazione, per il motivo appena citato. Siccome si tratta di una costante, possiamo indicarla con un simbolo. Si usa per questo la lettera i. Dal seguente esempio capirete perché si chiama unità immaginaria. -9=
-9= (9(-1))=
(9(-1))= 9
9 -1=
-1=3*i
Più in generale:
 -a=
-a= a*i
a*iQuindi tutti i risultati dell' operazione radice sono il risultato della moltiplicazione di un numero reale con i. Chiamo l' insieme dei risultati della moltiplicazione di un numero reale con i insieme dei numeri immaginari. 0 è anche un numero immaginario perché è il risultato di 0*i.
È veramente brutto dal punto di vista della notazione che la lettera i, che denota l' unità immaginaria, sia comunque liberamente usata come variabile. i è un particolare numero (ed è importante!) e dovrebbe avere il suo simbolo apposito. Appunto sarebbe stato opportuno inventare un nuovo simbolo e non utilizzare una lettera dell' alfabeto latino.
Moltiplicando e dividendo numeri immaginari ottengo numeri reali.
Esempi:
(5*i)(3*i)=
5*i*3*i=
5*3*i2=
15*(-1)= (per definizione di unità immaginaria)
-15
(8*i)/(3*i)=
8*i/3/i=
8*i*(1/3)*(1/i)=
8*(1/3)*i*(1/i)=
(8/3)*(i/i)=
(8/3)*1=
8/3
Moltiplicando e dividendo numeri reali con numeri immaginari ottengo numeri immaginari.
Esempi:
6*(5*i)=
6*5*i=
30*i
(2*i)/3=
2*i*(1/3)=
2*(1/3)*i=
(2/3)*i
9/(3*i)=
9/3/i=
3/i=
(3/i)*1=
(3/i)*(i/i)=
3*(1/i)*i*(1/i)=
3*i*(1/i)2=
3*i*(12/i2)=
3*i*(1/(-1))=
3*(1/(-1))*i=
(3/(-1))*i=
(-3)*i
Addizionando e sottraendo numeri immaginari ottengo numeri immaginari.
Esempi:
(5*i)+(6*i)=
5*i+6*i=
(5+6)*i=
11*i
(6*i)-(9*i)=
6*i-9*i=
(6-9)*i=
(-3)*i
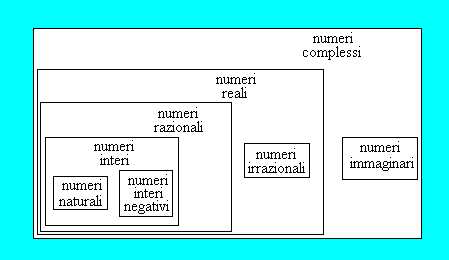
I problemi nascono quando usiamo le operazioni addizione e sottrazione tra un numero reale ed un numero immaginario. Infatti non sappiamo scrivere in un altra forma queste operazioni. Il risultato in questo caso può non essere né un numero reale né un numero immaginario. Chiamo l' insieme dei risultati delle operazioni addizione e sottrazione tra un numero reale ed un numero immaginario insieme dei numeri complessi. Tutti i numeri complessi si scrivono nella forma a+b*i, dove a e b sono numeri reali (per definizione). L' insieme dei numeri complessi è l' insieme di tutti i numeri, non ce ne sono altri (i numeri reali o rispettivamente gli immaginari si ottengono quando b=0 o rispettivamente a=0). Si calcola con i numeri complessi con le normali regole algebriche considerando i come una qualsiasi lettera.
Esempio:
(a+bi)(c+di)=
a(c+di)+bi(c+di)= (proprietà distributiva)
ac+adi+bic+bidi= (di nuovo prop. distr.)
ac+(ad+bc)i+bdi2= (di nuovo prop. distr.)
ac+(ad+bc)i+bd(-1)=
ac+(ad+bc)i+(-bd)=
ac+(-bd)+(ad+bc)i=
ac-bd+(ad+bc)i
Non serve usare questa formula per moltiplicare 2 numeri complessi, basta rifare gli stessi passaggi logici con i numeri al posto di a, b, c, d.
Può essere utile sapere che
 i=
i= 2/2(1+i).
2/2(1+i).I numeri reali si rappresentano su un sistema di coordinate cartesiane in una dimensione, cioè con un solo asse sul quale ogni punto rappresenta un numero reale. Allora si può immaginare che su questo asse "non c' è spazio" per i numeri complessi non reali. Infatti i numeri complessi si rappresentano nel piano; questo particolare piano si chiama piano complesso. Per convenzione il numero complesso a+b*i si rappresenta con il punto di coordinate cartesiane (a;b). Questa definizione va bene anche per i numeri complessi della forma a-b*i. Infatti:
a-b*i=
a+(-b*i)
In questo caso le coordinate cartesiane sono (a;(-b)).
Guardate sul disegno la rapresentazione dei numeri complessi 4+3*i, (-5)+i, (-4)-3*i e 2-4*i.

 . Qui per motivi tecnici di linguaggio HTML user� la notazione con (a+b*i).
. Qui per motivi tecnici di linguaggio HTML user� la notazione con (a+b*i).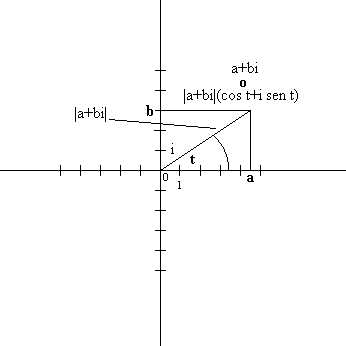
 ,
,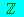 ,
, ,
, ,
, ,
,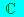 .
.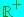 che indica i numeri reali positivi e analoghe.
che indica i numeri reali positivi e analoghe.