Regole algebriche

Nota: in questa pagina non sarà mai omesso il simbolo di moltiplicazione (ce ne sarà una sovrabbondanza) perché appunto si tratterà delle regole di calcolo e così sarà tutto più chiaro.
Per gli studenti le regole contenute in questa pagina e nelle 2 seguenti sono "il grosso" della matematica (se escludiamo la geometria), anzi sono proprio esse ad essere associate alla parola matematica. Sono state sempre presentate come un' elenco interminabile e di solito gli studenti le imparano semplicemente a memoria con la pratica dei conti, ma a volte hanno dubbi su di esse e sbagliano i conti. Il mio intento è far vedere che qui c' è pochissimo da imparare a memoria perché sono tutte strettamente collegate tra loro e alcune sono molto intuitive. Il legame tra loro si vede confrontandole con la tabella delle operazioni che qui copio per visualizzarlo meglio.

Basilari Per tornare indietro (1) Per tornare indietro (2)
1� livello Addizione, + Sottrazione, - Sottrazione, -
2� livello Moltiplicazione, * Divisione, / Divisione, /
3� livello Potenza, niente simbolo Radice, niente simbolo Logaritmo, niente simbolo
... ... ... ...

Proprietà delle operazioni
Qui enuncio in generale alcune delle proprietà fondamentali che possono soddisfare le operazioni per dar loro un nome. Queste diventeranno poi proprietà concrete di "vere" operazioni. Perciò se vi sembrano complicate, saltate al paragrafo Regole algebriche fondamentali e poi tornate indietro per vedere che ho scritto in generale delle proprietà particolari.
Userò i simboli ɘ e § per indicare delle operazioni generiche (ciascuno sta al posto di un simbolo di operazione, ad esempio +).
Proprietà associativa: (aɘb)ɘc=aɘ(bɘc)
Proprietà commutativa: aɘb=bɘa
Proprietà distributiva destra di § rispetto a ɘ: (aɘb)§c=(a§c)ɘ(b§c)
Proprietà distributiva sinistra di § rispetto a ɘ: c§(aɘb)=(c§a)ɘ(c§b)
Chiaramente se § è commutativa, allora le proprietà distibutive destra e sinistra di § rispetto a ɘ sono equivalenti e le chiamiamo proprietà distibutiva di § rispetto a ɘ.

Regole algebriche fondamentali
1� livello
 --1 proprietà associativa
(a+b)+c=a+(b+c)=a+b+c
 --2 proprietà commutativa
a+b=b+a
 --3
a+b=a-(-b)
a-b=a+(-b)
 Con questa regola possiamo trasformare la sottrazione in addizione e così possiamo usare tutte le proprietà dell' addizione.
Dalla prima segue
-(-q)=0+q=q
 -(-q)=q
 --4
regola più generale
a-(b1+b2+...+bn)=a-b1-b2-...-bn
 regola più specifica
a-(b+c)=a-b-c
 --5
a-a=0
 2� livello
 --1 proprietà associativa
(a*b)*c=a*(b*c)=a*b*c
 --2 proprietà commutativa
a*b=b*a
 --3
a*b=a/(1/b)
a/b=a*(1/b)
 Con questa regola possiamo trasformare la divisione in moltiplicazione e così possiamo usare tutte le proprietà della moltiplicazione.
Dalla prima segue
1/(1/q)=1*q=q
 1/(1/q)=q
 --4
regola più generale
a/(b1*b2*...*bn)=a/b1/b2/.../bn
 regola più specifica
a/(b*c)=a/b/c
 --5
a/a=1
 --6
-a=(-1)*a
 Da questa segue
 (-a)*b=(-1)*a*b=-a*b
a*(-b)=(-1)*a*b=-a*b
(-a)*(-b)=a*b
 --7 proprietà distributiva della mooltiplicazione rispetto alla somma
regola più generale
(a1+a2+...+an)*c=a1*c+a2*c+...+an*c
 regola più specifica
(a+b)*c=a*c+b*c
 Da questa seguono (ed è intuitivo che valgano se vale la regola sopra):
(a-b)*c=(a+(-b))*c=a*c+(-b)*c=a*c+(-b*c)=a*c-b*c
(a+b)/c=(a+b)*(1/c)=a*(1/c)+b*(1/c)=a/c+b/c
(a-b)/c=(a-b)*(1/c)=a*(1/c)-b*(1/c)=a/c-b/c
Quindi
 (a-b)*c=a*c-b*c
(a+b)/c=a/c+b/c
(a-b)/c=a/c-b/c
 La proprietà distributiva coinvolge questo e il livello precedente di operazioni.
3� livello
 --1 proprietà associativa
non vale
--2 proprietà commutativa
non vale
--3
ab=a
a=a(1/b)
 Con questa regola possiamo trasformare l' operazione radice in operazione potenza e così possiamo usare tutte le proprietà dell' operazione potenza.
--4
non vale
--5
logaa=1
 --6a
(-a)b=ab se b è un numero intero pari
(-a)b=(-1)*ab se b è un numero intero dispari
Se la base è negativa, la potenza è definita solo se l' esponente è un numero intero.
 a(-b)=1/ab
 (-a)(-b)=1/(-a)b=1/ab se b è un numero intero pari
(-a)(-b)=
1/(-a)b=
1/((-1)*ab)=
1/(-1)/ab=
(1/(-1))/ab=
(-1)/ab
se b è un numero intero dispari
Quindi
 (-a)(-b)=1/ab se b è un numero intero pari
(-a)(-b)=(-1)/ab se b è un numero intero dispari
 --6b
(1/a)b=1/(ab)
 (1/a)b=
(1/a)*(1/a)*(1/a)*...*(1/a)*(1/a)= (b volte)
1/a/a/a/.../a/a= (b volte)
1/(a*a*a*...*a*a)= (b volte)
1/(ab)
 --7 proprietà distributiva destra ddella potenza rispetto alla moltiplicazione
(purtroppo non vale quella sinistra)
regola più generale
(a1*a2*...*an)c=a1c*a2c*...*anc
 regola più specifica
(a*b)c=ac*bc
 Da questa seguono (ed è intuitivo che valgano se vale la regola sopra):
(a/b)c=(a*(1/b))c=ac*(1/b)c=ac*(1/bc)=ac/bc
(a*b)=(a*b)(1/c)=a(1/c)*b(1/c)=a*b
(a/b)=(a/b)(1/c)=a(1/c)/b(1/c)=a/b
Quindi
 (a/b)c=ac/bc
(a*b)=a*b
(a/b)=a/b
 La proprietà distributiva coinvolge questo e il livello precedente di operazioni.
--8
a(b+c)=ab*ac
 Da questa segue
 a(b-c)=ab/ac
 --9
a(b*c)=(ab)c
 Da questa segue
 a(b/c)=(ab)
 --10
loga(ab)=b
b(logba)=a
 --11
logc(a*b)=logca+logcb
logc(a/b)=logca-logcb
 --12
logc(ab)=b*logca
logc(a)=(1/b)*logca
 --13
logba=logca/logcb
Prodotti notevoli
--1
(a+b)*(c+d)=a*c+a*d+b*c+b*d
(a+b)*(c-d)=a*c-a*d+b*c-b*d
(a-b)*(c+d)=a*c+a*d-b*c-b*d
(a-b)*(c-d)=a*c-a*d-b*c+b*d
 Per dimostrare la prima si usa la proprietà distributiva 2 volte.
(a+b)*(c+d)=
a*(c+d)+b*(c+d)=
a*c+a*d+b*c+b*d
 Di queste basta sapere la prima, le altre si possono ottenere facilmente ogni volta dalle regole fondamentali trasformando l' operazione addizione in sottrazione. Ecco l' esempio per una di esse:
(a-b)*(c-d)=
(a+(-b))*(c+(-d))= (applico la prima di queste regole)
a*c+a*(-d)+(-b)*c+(-b)*(-d)=
a*c+(-a*d)+(-b*c)+b*d=
a*c-a*d-b*c+b*d
 --2
(a+b)*(a-b)=a2-b2
 (a+b)*(a-b)=
(a+b)*(a+(-b))=
a*(a+(-b))+b*(a+(-b))=
a*a+a*(-b)+b*a+b*(-b)=
a2+(-a*b)+a*b+(-b*b)=
a2+a*b+(-a*b)+(-b2)=
a2+(-b2)+(a*b-a*b)=
a2-b2+0=
a2-b2
 --3
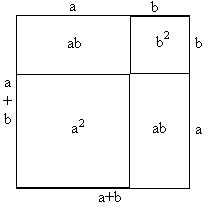
(a+b)2=a2+2*a*b+b2
 (a+b)2=
(a+b)*(a+b)=
a*(a+b)+b*(a+b)=
a*a+a*b+b*a+b*b=
a2+a*b+a*b+b2=
a2+1*(a*b)+1*(a*b)+b2
a2+(1+1)*(a*b)+b2
a2+2*a*b+b2
 Come per la prima di queste regole non serve imparare anche quanto fa (a-b)2, perché si può ottenere facilmente ogni volta dalle regole fondamentali trasformando l' operazione addizione in sottrazione.
Questa regola si può vedere anche graficamente considerando che un rettangolo di lati a e b ha area a*b.
--4
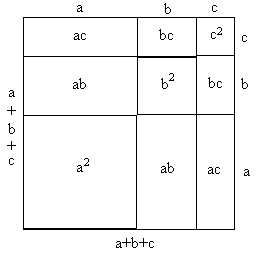
(a+b+c)2=a2+b2+c2+2*a*b+2*a*c+2*b*c
 (a+b+c)2=
(a+(b+c))2= (applico la regola precedente)
a2+2*a*(b+c)+(b+c)2
a2+2*a*b+2*a*c+b2+2*b*c+c2=
a2+b2+c2+2*a*b+2*a*c+2*b*c
 Come per la precedente di queste regole non serve imparare anche quanto fa (a-b-c)2 o (a+b-c)2 o qualcosa di simile, perché si può ottenere facilmente ogni volta dalle regole fondamentali trasformando l' operazione addizione in sottrazione.
Questa regola si può vedere anche graficamente considerando che un rettangolo di lati a e b ha area a*b.
--5
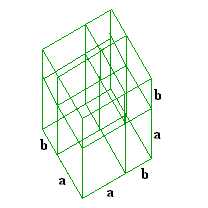
(a+b)3=a3+3*a2*b+3*a*b2+b3
 (a+b)3=
(a+b)(2+1)=
(a+b)2*(a+b)1=
(a+b)2*(a+b)=
(a2+2*a*b+b2)*(a+b)= (applico la prima di queste regole in una forma un po' più generale)
a2*a+a2*b+2*a*b*a+2*a*b*b+b2*a+b2*b=
a2*a1+a2*b+2*a2*b+2*a*b2+a*b2+b2*b1=
a(2+1)+1*(a2*b)+2*(a2*b)+2*(a*b2)+1*(a*b2)+b(2+1)=
a3+(1+2)*a2*b+(2+1)*a*b2+b3=
a3+3*a2*b+3*a*b2+b3
 Questa regola si può vedere anche graficamente considerando che un cuboide di lati a, b e c ha volume a*b*c.
--6
(a-b)*(a2+a*b+b2)=a3-b3
(a-b)*(a2-a*b+b2)=a3+b3
 La dimostrazione di questa regola funziona come le dimostrazioni delle regole precedenti.
Intuizione applicata alle regole algebriche fondamentali
1� livello
--1
La proprietà associativa per l' addizione è molto inuitiva. Se ho molte quantità e voglio unirle, se le riunisco subito tutte insieme o se prima le unisco in gruppi in modi diversi, la quantità che avrò alla fine non cambierà.
--2
La proprietà commutativa per l' addizione è molto intuitiva. Se prendo una prima quantità e le aggiungo una seconda otterrò lo stesso che se alla seconda quantità aggiungo la prima.
--3
Se abbiamo il numero a, -a è il suo opposto, cioè si trova dalla parte opposta dello 0 alla stessa distanza. Allora l' opposto di 0 è 0 stesso. L' idea stessa di "negatività" indica qualcosa che va al contrario di come dovrebbe andare. Perciò è abbastanza intuitivo capire che sottrarre un numero negativo è come sommare un numero positivo opposto al precedente e che sommare un numero negativo è come sottrarre un numero positivo opposto al precedente: questa è la regola a-(-b)=a+b e a+(-b)=a-b se consideriamo a e b numeri positivi, ma vale anche se sono negativi. È chiaro che l' opposto dell' opposto è il numero stesso, quindi diventa evidente la regola -(-q)=q.
--4
La regola a-b1-b2-...-bn=a-(b1+b2+...+bn) è molto intuitiva. Pensate: abbiamo una quantità alla quale togliamo qualcosa, poi qualcos' altro, poi qualcos' altro e così avanti. Ma è lo stesso se mettiamo insieme tutte le quantità da togliere e togliamo tutto questo dalla quantità iniziale.
--5
È chiaro che a-a=0. Se prendiamo una quantità e togliamo la quantità stessa non ci rimane niente.
2� livello
--1
La proprietà associativa per la moltiplicazione è meno intuitiva di quella per l' addizione. Perciò ricordatevi che se cambiate l' ordine in cui raggruppate delle quantità mentre fate una sequenza di moltiplicazioni, il risultato non cambia. Nel caso della moltiplicazione di 3 quantità c' è un modo di vedere questa proprietà: immaginate ciascuna come lunghezza di un lato di un cuboide; è chiaro che se girate il cuboide in modo da avere diversi lati che prendono ruolo di lati del rettangolo di base, il volume del cuboide non cambia.
--2
La proprietà commutativa per la moltiplicazione è meno intuitiva di quella per l' addizione. Infatti chi mi assicura, nel caso di 3*5, che 5+5+5=3+3+3+3+3? Perciò ricordatevi che se scambiate l' ordine in cui fate una sequenza di moltiplicazioni, il risultato non cambia. Comunque potete vedere questa proprietà come nel caso precedente e anche per 2 quantità se le pensate come lati di un rettangolo.
--3
Anche questa proprietà non è molto intuitiva, ma si può fare un' analogia con la medesima del primo livello. Qui invece di opposto c' è il concetto di inverso. Se abbiamo il numero a, 1/a è il suo inverso. Perciò è abbastanza intuitivo capire che dividere con l' inverso di un numero è come moltiplicare con quel numero e che moltiplicare con l' inverso di un numero è come dividere con quel numero. È chiaro che l' inverso dell' inverso è il numero stesso, quindi diventa evidente la regola 1/(1/q)=q.
--4
La regola a/b1/b2/.../bn=a/(b1*b2*...*bn) è molto intuitiva. Pensate: abbiamo una quantità, la dividiamo un certo numero di volte, poi ancora, poi ancora e così avanti. Ma è lo stesso se moltiplichiamo tutti questi numeri e dividiamo la quantità iniziale con ciò che abbiamo ottenuto dalla moltiplicazione.
--5
È chiaro che a/a=1. Se valutiamo quante volte una quantità sta in se stessa (per definizione di divisione) otteniamo esattamente 1.
--6
Questa regola è molto intuitiva. Se moltiplichiamo una quantità con 1, otteniamo di nuovo la stessa quantità (guarda più sotto). Allora possiamo immaginare che moltiplicando una quantità con -1, essa diventerà il proprio opposto. Le regole
(-a)*b=(-1)*a*b=-a*b
a*(-b)=(-1)*a*b=-a*b
(-a)*(-b)=a*b
che ne sono conseguenza sono anche abbastanza intuitive. Se moltiplicando con -1 otteniamo l' opposto, allora moltiplicando con -a otteremo l' opposto a volte (-a*b è chiaramente l' opposto di a*b). Da tutto ciò sembra evidente che se moltiplichiamo 2 numeri positivi otterremo un numero positivo, se moltiplichiamo un positivo ed un negativo (non importa l' ordine perché vale la proprietà commutativa) otterremo un negativo e se moltiplichiamo 2 negativi otteremo un positivo (un certo numero di volte l' opposto di un negativo è chiaramente un positivo). Queste sono le regole appena scritte se consideriamo a e b positivi (ma vale anche se sono negativi).
--7
In realtà la proprietà distributiva è molto intuitiva e la usiamo senza rendercene conto. Se io chiedo a qualcuno di calcolarmi quanto fa 3*13, quasi sicuramente ragionerà in questo modo:
3*13=3*(10+3)=3*10+3*3=30+9=39
Se invece chiedo quanto fa 96/3:
96/3=(90+6)/3=90/3+6/3=30+2=32
Se invece chiedo quanto fa 99*6:
99*6=(100-1)*6=100*6-1*6=600-6=594
3� livello
--1
-
--2
-
--3
Sembra strano, ma dobbiamo di nuovo considerare l' inverso come per il secondo livello; si può fare un' analogia con la medesima regola al primo ed al secondo livello. È abbastanza intuitivo capire che applicare l' operazione radice con l' inverso di un numero come esponente è come applicare l' operazione potenza con quel numero come esponente e che applicare l' operazione potenza con l' inverso di un numero come esponente è come applicare l' operazione radice con quel numero come esponente.
--4
-
--5
Se ab=c, b si calcola così (per definizione): b=logac.
Quindi se logqq=1 (ho cambiato lettera per non fare confusione), q1=q, il che è sempre vero.
--6a
Le regole
(-a)b=ab se b è un numero intero pari
(-a)b=(-1)*ab se b è un numero intero dispari
sono abbastanza intuitive. Immagino a come positivo e allora -a è negativo. Moltiplico -a b volte. È chiaro che otterrò ab o il suo opposto. Ma sarà positivo o negativo? Usando la proprietà associativa raggruppo 2 a 2 i termini della moltiplicazione; se b è dispari, rimarrà isolato un termine, se b è pari avremo solo coppie di numeri moltiplicati. Il risultato della moltiplicazione di ogni coppia sarà positivo (perché moltiplichiamo 2 numeri negativi fra loro), perciò moltiplicando tutte queste coppie otterremo ancora qualcosa di positivo; se b è pari il risultato sarà quindi positivo, se è dispari il risultato sarà dato dalla moltiplicazione di un numero positivo (il risultato delle coppie) con un negativo, quindi otterremo un numero negativo.
Non si riesce a vedere intuitivamente la regola a(-b)=1/ab. Le altre seguono da essa.
--6b
Sembra ragionevole che prendendo l' inverso di un numero e facendone l' operazione potenza con un' altro otteniamo l' "inverso" dell' operazione potenza tra il primo ed il secondo numero. È comunque utile guardare la dimostrazione algebrica in questo caso.
--7
È molto intuitivo che valga la proprietà distributiva destra: (a*b)c=ac*bc.
L' espressione sopra si può pensare come una sequenza del tipo
a*b*a*b*a*b*...*a*b*a*b=a*a*a*...*a*a*b*b*b*...*b*b dove ci sono c ripetizioni.
È chiaro che vale l' uguaglianza perché vale la proprietà commutativa. Le altre forme della proprietà distributiva sono conseguenza di questa.
--8
È molto intuitivo che valga a(b+c)=ab*ac.
L' espressione sopra si può pensare come una sequenza del tipo
a*a*a*...*a*a=(a*a*a*...*a*a)*(a*a*a*...*a*a) dove a sinistra dell' uguaglianza ci sono b+c ripetizioni e a destra ci sono b ripetizioni per la prima parentesi e c ripetizioni per la seconda. È chiaro che vale l' uguaglianza perché vale la proprietà associativa.
--9
È molto intuitivo che valga a(b*c)=(ab)c.
L' espressione sopra si può pensare come una sequenza del tipo
a*a*a*...*a*a=(a*a*a*...*a*a)*(a*a*a*...*a*a)*(a*a*a*...*a*a)*...*(a*a*a*...*a*a)*(a*a*a*...*a*a) dove a sinistra dell' uguaglianza ci sono b*c ripetizioni e a destra ci sono b ripetizioni in ogni parentesi e c ripetizioni di parentesi. È chiaro che vale l' uguaglianza perché vale la proprietà associativa.
--10
Se ab=c, b si calcola così (per definizione): b=logac.
Riscriviamo la regola con altre lettere (per non fare confusione):
logp(pq)=q
q(logqp)=p
Queste significano (per definizione): pq=pq
logqp=logqp
Evidentemente sono sempre vere.
--
Le successive si possono dimostrare dalla definizione ma non sono intuitive.
Note sul calcolo numerico
--Le sottrazioni che danno come risultatto un numero negativo o le sottrazioni da un numero già negativo si effettuano immaginando la retta dei numeri (un asse di un sistema di coordinate). Sommare significa spostarsi a destra, sottrarre significa spostarsi a sinistra.
Esempio:
(-5)-3=-8
Ci troviamo 5 posti a sinistra dello 0 e ci spostiamo di altri 3 posti a sinistra: arriveremo ad 8 posti a sinistra dello 0.
--1*a=a
La moltiplicazione è un' addizione ripetuta. Ad esempio 4*a=a+a+a+a, 2*a=a+a. Ma se abbiamo 1? L' addizione non si effettua affatto e lasciamo scritto a.
--a/1=a
Se facciamo questa divisione stiamo valutando (per definizione) quante volte il numero 1 sta in a: chiaramente a volte.
--0*a=0
La moltiplicazione è un' addizione ripetuta. In questo caso non si effettua alcuna addizione, ma non abbiamo nemmeno 1 elemento, come nel caso di 1*a, bensì l' elemento neutro per l' addizione, cioè quell' elemento che nell' addizione lascia tutto invariato, quindi 0.
--Frazioni
La nostra idea intuitiva di frazione si può esprimere attraverso l' operazione divisione. Ad esempio mezzo, tre quarti, tre quinti, sei decimi, cinque centesimi sono equivalenti alle espressioni 1:2, 3:4, 6:10, 5:100. A prima vista sembrano cose diverse, perciò vediamolo in un esempio. 4 persone devono dividersi equamente 3 pizze. Quanto riceve ciascuno? È chiaro che bisogna dividere (lo dice la parola stessa, stiamo dividendo delle pizze tra alcune persone) il numero di pizze con il numero di persone (non il contrario: le pizze vanno distibuite tra le persone, non il viceversa). Quindi il risultato è 3:4 che possiamo lasciare scritto così perché come risultato non dà un numero intero ma che possiamo anche scrivere 0,75 perché questo non è un valore approssimato ma esatto. Però ho detto che 3:4 è equivalente a tre quarti. Quindi ognuno dovrebbe ricevere tre quarti di pizza. È vero? Sì. Immaginiamo di tagliare via un quarto da ciascuna delle 3 pizze iniziali; i 3 pezzi messi insieme daranno di nuovo tre quarti di pizza e così tutti riceveranno la stessa quantità.
Le frazioni sono sempre numeri razionali perché per definizione una frazione è un' espressione della forma a/b, dove a e b sono numeri interi. a si chiama numeratore (perché dice quante parti si prendono in considerazione) e b denominatore (perché dà il nome alla frazione). Se a o b fossero irrazionali, l' espressione semplicemente non si chiamerebbe più frazione (infatti la nostra idea intuitiva verrebbe meno), però potremmo sempre trasformarla in modo da ottenere una moltiplicazione tra un razionale ed un irrazionale. Gli irrazionali che si incontrano più frequentemente sono risultati di operazioni radice che non danno numeri interi; ce ne sono altri ma limitiamoci a vedere esempi su questo caso.
3/6=1*3*(1/6)=3*(1*(1/6))=3*(1/6)
6*5/7=5*6*(1/7)=5*(6/7)
17/(4*5)=17/4/5=(17/4)*(1/5)=(1/5)*(17/4)
Nell' ultimo esempio l' espressione 1/5 non è una frazione, ma è scritta come se lo fosse. Perciò è meglio trasformarla per eliminare l' operazione divisione (in pratica vogliamo scrivere tutto in forma di moltiplicazione tra una frazione ed un irrazionale espresso con una radice). Si dice che si razionalizza la frazione. Alcuni esempi di razionalizzazione:
17/(4*5)=
17/(4*5)*1=
17*(1/(4*5))*5*(1/5)=
17*5*(1/4/5)*(1/5)=
17*5*((1/4)*(1/5))*(1/5)=
5*17*(1/4)*(1/5)2=
5*17*(1/4)*(12/(5(1/2))2)=
5*17*(1/4)*(1/5(1/2)*2)=
5*17*(1/4)*(1/51)=
5*17*(1/4)*(1/5)=
5*(17/4/5)=
5*(17/(4*5))=
5*(17/20)

1/5=
1/5*1=
1/5*(5)2*(1/(5)2)=
(5)2*(1/5)*(12/(5)2)=
(5)2*(1/5)1*(1/5)2=
(5)2*(1/5)(1+2)=
(5)2*(1/5)3=
(5)2*(13/(5(1/3))3)=
(5)2*(1/5(1/3)*3)=
(5)2*(1/51)=
(5)2*(1/5)

Per il successivo esempio bisogna considerare la regola 2 dei prodotti notevoli.
6/(3+1)=
6/(3+1)*1=
6*(1/(3+1))*(3-1)*(1/(3-1))=
6*(3-1)*(1/(3+1)/(3-1))=
6*(3-1)*(1/((3+1)*(3-1)))=
6*(3-1)*(1/(32-12))=
6*(3-1)*(1/((3(1/2))2-1))=
6*(3-1)*(1/(3(1/2)*2-1))=
6*(3-1)*(1/(31-1))=
6*(3-1)*(1/(3-1))=
6*(3-1)*(1/2)=
6*(1/2)*(3-1)=
(6/2)*(3-1)=
3*(3-1)
Questi sono gli esempi più tipici di razionalizzazione. Razionalizzare un' espressione significa togliere l' operazione radice dal denominatore di una frazione.
 Per fare i conti con le frazioni sono sufficienti le regole algebriche fondamentali, ma farò vedere come ci si può semplificare i conti.
Se si moltiplica o divide il numeratore e il denominatore con lo stesso numero, la frazione rimane la stessa. Sembra strano? Una frazione è pur sempre una divisione, quindi valutiamo quante volte il denominatore sta nel numeratore; questo numero di volte non cambia se moltiplichiamo o dividiamo entrambi con lo stesso numero. Ad esempio 3/4 e 6/8 sono frazioni equivalenti: infatti se prendiamo 3 parti su 4 di qualcosa (ad esempio una pizza) è lo stesso che se prendiamo 6 parti su 8. Ciò risulta molto utile se vogliamo addizionare o sottrarre frazioni. Esempio:
5/6+4/9=
(5*3)/(6*3)+(4*2)/(9*2)=
15/18+8/18=
(15+8)/18=
23/18
Come facciamo a vedere subito con quale numero moltiplicare il numeratore e il denominatore di ogni frazione? Intanto osserviamo che vogliamo far diventare tutti i denominatori uguali per applicare la proprietà distributiva. Perciò scomponiamo i denominatori in una moltiplicazione di numeri che non si possono ulteriormente scomporre. Tali numeri si chiamano numeri primi. I numeri primi sono quelli divisibili solo con 1 e con se stessi (quindi è chiaro che non si possono scomporre in una moltiplicazione di altri numeri). Per scomporre i denominatori bisogna sapere quali sono i primi numeri primi.
Numeri primi: 2, 3, 5, 7, 11, 13, 17, 19, 23, 27, 29, 31, 37, 41, 43, 47, 53, ...
Se ve ne servono altri potete trovarli abbastanza facilmente.
Per scomporre un numero (se non è un numero primo) si fa così: si prende il numero e lo si divide con 2 se è possibile (cioè se la divisione dà un numero intero), diversamente lo si divide con 3 se è possibile, diversamente si prova sempre con un nuovo numero primo nell' ordine crescente; quando abbiamo effettuato una divisione proviamo a dividere il risultato con lo stesso numero primo se è possibile oppure con un nuovo sempre nell' ordine crescente; proseguiamo così fino a che otteniamo 1 come risultato di una divisione; il numero di partenza è uguale alla moltiplicazione dei numeri primi con i quali abbiamo diviso (è una conseguenza diretta della regola 4 del secondo livello). Ciò si può effettuare in modo schematico. Lo faccio vedere in qualche esempio.
60 - 2           350 - 2                45 - 3
30 - 2           175 - 5                15 - 3
15 - 3            35 - 5                 5 - 5
 5 - 5             7 - 7                 1
1                  1
Quindi 60=2*2*3*5    Quindi 350=2*5*5*7    Quindi 45=3*3*5
Poi basta confrontare le scomposizioni dei vari denominatori per capire con che numero moltiplicare ogni frazione. Esempio:
13/60+35/140 Scomponiamo 140 (60 è stato scomposto sopra):
140 - 2
 70 - 2
 35 - 5
  7 - 7
  1
Confrontiamo: 60=2*2*3*5, 140=2*2*5*7. È chiaro che moltiplicheremo la prima frazione con 7, la seconda con 3.
13/60+35/140=
(13*7)/(60*7)+(35*3)/(140*3)=
91/420+105/420=
(91+105)/420=
196/420
Probabilmente la frazione sopra si può semplificare. Per vedere se è possibile scomponiamo in fattori il numeratore (la scomposizione del denominatore è evidente da quanto scrive sopra).
196 - 2
 98 - 2
 49 - 7
  7 - 7
  1
Confrontiamo: 196=2*2*7*7, 420=2*2*3*5*7. È chiaro che possiamo dividere entrambi con 2*2*7.
196/420=
((2*2*7*7)/(2*2*7))/((2*2*3*5*7)/(2*2*7))=
((2*2*7*7)/2/2/7)/((2*2*3*5*7)/2/2/7)=
(2*2*7*7*(1/2)*(1/2)*(1/7))/(2*2*3*5*7*(1/2)*(1/2)*(1/7))=
(2*(1/2)*2*(1/2)*7*(1/7)*7)/(2*(1/2)*2*(1/2)*7*(1/7)*3*5)=
(1*1*1*7)/(1*1*1*3*5)=
7/(3*5)=
7/15
Avremmo potuto dividere semplicemente il numeratore ed il denominatore, ma ho scritto il conto sopra perché non è facile dividere a memoria numeri così grandi (quindi fate così se avete paura di sbagliare i conti).
196/420=
(196/28)/(420/28)=
7/15
Il risultato della moltiplicazione di 2 frazioni è una frazione che ha al numeratore il risultato della moltiplicazione dei numeratori e al denominatore il risultato della moltiplicazione dei denominatori. Questo si può dimostrare dalle regole algebriche fondamentali. Esempi:
(3/5)*(7/2)=
(3*7)/(5*2)=
21/10

(1/60)*(12/7)=
(1*12)/(60*7)=
(2*2*3)/(2*2*3*5*7)=
((2*2*3)/(2*2*3))/((2*2*3*5*7)/(2*2*3))=
1/((2*2*3*5*7)/2/2/3)=
1/(2*2*3*5*7*(1/2)*(1/2)*(1/3))=
1/(2*(1/2)*2*(1/2)*3*(1/3)*5*7)=
1/(1*1*1*5*7)=
1/(5*7)=
1/35

1/(a/b)=b/a
 1/(a/b)=
1/(a*(1/b))=
1/a/(1/b)=
(1/a)*(1/(1/b))=
(1/a)*b=
b*(1/a)=
b/a
 Adesso sappiamo dividere facilmente frazioni. Esempio:
(5/7)/(2/3)=
(5/7)*(1/(2/3))=
(5/7)*(3/2)=
(5*3)/(7*2)=
15/14
--Semplificare espressioni con l' operazzione radice
Come si può semplificare 108?
Intanto si scompone in fattori 108.
108 - 2
54  - 2
27  - 3
9   - 3
3   - 3
1
Quindi 108=2*2*3*3*3.
108=
(2*2*3*3*3)=
(22*32*3)=
(22)*(32)*3=
(22)1/2*(32)1/2*3=
22*(1/2)*32*(1/2)*3=
21*31*3=
2*3*3=
6*3
Un' altro esempio: 24
24 - 2
12 - 2
6  - 2
3  - 3
1
Quindi 24=2*2*2*3.
24=
(2*2*2*3)=
(23*3)=
(23)(1/3)*3=
23*(1/3)*3=
21*3=
2*3
--1a=1
L' espressione sopra si può scrivere 1*1*1*...*1*1=1. Ciò è sempre vero, infatti 1*1=1.
--a1=a
L' operazione potenza è una moltiplicazione ripetuta. Ad esempio a4=a*a*a*a, a2=a*a. Ma se abbiamo 1? La moltiplicazione non si effettua affatto e lasciamo scritto a.
--0a=0
L' espressione sopra si può scrivere 0*0*0*...*0*0=0. Ciò è sempre vero, infatti 0*0=0.
--a0=1
L' operazione potenza è una moltiplicazione ripetuta. In questo caso non si effettua alcuna moltiplicazione, ma non abbiamo nemmeno 1 elemento, come nel caso di a1, bensì l' elemento neutro per la moltiplicazione, cioè quell' elemento che nella moltiplicazione lascia tutto invariato, quindi 1.
Comunque si può anche vedere dalla regola 8 del terzo livello.
a0=a(b-b)=ab/ab=1.
--Operazione logaritmo
Per l' operazione logaritmo si considerano quasi esclusivamente (ma non solo) i casi log10a=log a o logea=ln a dove e sta ad indicare una costante (un numero irrazionale). e~2,71828182845. Gli altri casi si possono però calcolare da questi applicando la regola 13 del terzo livello. Ciò vi serve se volete calcolare un' operazione logaritmo con la calcolatrice. Di solito per log a si usa il tasto log, per ln a si usa il tasto ln, ma a volte anche il tasto log (in quest' ultimo caso non c' è la possibilità di calcolare con la calcolatrice log10a).
È veramente brutto dal punto di vista della notazione che la lettera e sia comunque liberamente usata come variabile. e è un particolare numero (ed è importante!) e dovrebbe avere il suo simbolo apposito. Appunto sarebbe stato opportuno inventare un nuovo simbolo e non utilizzare una lettera dell' alfabeto latino.
 logba=logca/logcb
Esempio:
log311=
log1011/log1033~
1,04/0,48~
2,17
oppure
log311=
loge11/loge33~
2,40/1,10~
2,18
(Il risultato non è identico perché ho preso troppi pochi decimali.)
e è importante nella matematica per vari motivi, ma quello più famoso è che la funzione derivata della funzione ln x è 1/x, quindi ha una derivata molto semplice (qui non spiegherò cosa sono le funzioni derivate).
Come calcolare logq(-p) (con p positivo)?
Ci si accorge facilmente che il risultato non è un numero reale. Perciò si potrebbe pensare di prendere log (-1) come nuova unità immaginaria e calcolare gli altri casi con essa. Però la matematica superiore ci fornisce un risultato che ci fa capire che si tratta sempre degli stessi numeri immaginari e non di un nuovo insieme. Ebbene:
e(b*i)=cos b+i*sen b
 Da essa segue
e(a+b*i)=
ea*e(b*i)=
ea*(cos b+i*sen b)
e(a+b*i)=ea*(cos b+i*sen b)
 Ritorniamo alla prima formula per calcolare ln (-1)
e(b*i)=cos b+i*sen b /ln
b*i=ln (cos b+i*sen b)
ln (cos b+i*sen b)=b*i
Al posto di b metto
ln (cos +i*sen )=*i
ln ((-1)+i*0)=*i
ln ((-1)+0)=*i
ln (-1)=*i
ln (-1)=*i
 Esempi:
ln (-e)=
ln (-1*e)=
ln (-1)+ln e=
*i+1~
1+3,14*i

log (-10)=
log (-1*10)=
log (-1)+log1010=
ln (-1)/ln 10+1=
*i/ln 10+1~
1+1,36*i
Trucchetti per calcolare facilmente a memoria certe cose
È inevitabile che negli esempi dei trucchetti sottostanti si nascondano altri trucchetti di calcolo.
Innanzitutto bisogna sapere a memoria le tabelline.
* 1 2 3 4 5 6 7 8 9 10
1 1 2 3 4 5 6 7 8 9 10
2 2 4 6 8 10 12 14 16 18 20
3 3 6 9 12 15 18 21 24 27 30
4 4 8 12 16 20 24 28 32 36 40
5 5 10 15 20 25 30 35 40 45 50
6 6 12 18 24 30 36 42 48 54 60
7 7 14 21 28 35 42 49 56 63 70
8 8 16 24 32 40 48 56 64 72 80
9 9 18 27 36 45 54 63 72 81 90
10 10 20 30 40 50 60 70 80 90 100
Come calcolare facilmente a memoria cose come a*5 o a/5?
 a*5=(a*10)/2
a/5=(a/10)*2
 Esempi: 25*5=(25*10)/2=250/2=(200+50)/2=200/2+50/2=100+25=125
63/5=(63/10)*2=6,3*2=(6+0,3)*2=6*2+0,3*2=12+0,6=12,6
Come calcolare facilmente a memoria cose come a*50 o a/50?
 a*50=(a*100)/2
a/50=(a/100)*2
 Esempio: 9*50=(9*100)/2=900/2=(800+100)/2=800/2+100/2=400+50=450
Come calcolare facilmente a memoria cose come a*25 o a/25?
 a*25=(a*100)/4
a/25=(a/100)*4
 Esempio: 9*25=(9*100)/4=900/4=(800+100)/4=800/4+100/4=200+25=225
Come calcolare facilmente a memoria cose come t2, dove t è un numero a 2 cifre?
 Devo usare la formula (a+b)2=a2+b2+2*a*b in modo adeguato e devo usare anche la formula
(a-b)2=a2+b2-2*a*b che si ottiene facilmente dalla precedente (vedere sopra).
Esempi:
162=(10+6)2=102+62+2*10*6=100+36+12*10=136+120=256
432=(40+3)2=402+32+2*40*3=(4*10)2+9+24*10=
42*102+9+240=16*100+9+240=1 600+240+9=1 849
192=(2-1)2=202+12-2*20*1=(2*10)2+1-40=22*102+1-40=4*100+1-40=401-40=361
992=(100-1)2=1002+12-2*100*1=(102)2+1-200=104+1-200=10 001-200=9 801
Come calcolare facilmente a memoria cose come r-s, dove r e s sono numeri interi?
 Non è sempre facile vedere subito se si può utilizzare la formula (a+b)*(a-b)=a2-b2 per questo scopo.
Esempi:
100-36=102-62=(10+6)*(1-6)=16*4=2*(2*16)=2*32=64
81-49=92-72=(9+7)*(9-7)=16*2=32
64-25=82-52=(8+5)*(8-5)=13*3=(10+3)*3=10*3+3*3=30+9=39
36-81=62-92=(6+9)*(6-9)=15*(-3)=-15*3=-45
9-36=32-62=(3+6)*(3-6)=9*(-3)=-9*3=-27
169-81=132-92=(13+9)*(13-9)=22-4=18
225-121=152-112=(15+11)*(15-11)=26*4=2*(2*26)=2*(2*(20+6))=2*(2*20+2*6)=2*(40+12)=2*52=
2*(50+2)=2*50+2*2=100+4=104
Come calcolare facilmente a memoria cose come r*s, dove r ed s sono numeri a 2 cifre?
 Dobbiamo cercare di aiutarci con la proprietà distributiva per trovare cose del tipo t2, dove t è un numero a 2 cifre.
Esempi:
16*13=(13+3)*13=132+3*13=(10+3)2+3*(10+3)=102+32+2*10*3+3*10+3*3=100+9+60+30+9=190+18=208
forse conviene calcolare a parte 132
17*14=(14+3)*14=142+3*14=(10+4)2+3*(10+4)=102+42+2*10*4+3*10+3*4=100+16+80+30+12=210+28=238
forse conviene calcolare a parte 142
53*52=(52+1)*52=522+1*52=(50+2)2+52=(5*10)2+22+2*50*2+52=52*102+4+200+52=
25*100+4+200+52=2 500+4+200+52=2 756
forse conviene calcolare a parte 522
101*99=(99+2)*99=992+2*99=(10-1)2+2*(10-1)=1002+12-2*100*1+2*10-2*1=10 000+1-200+20-2=
10 001-2+20-200=9 999
forse conviene calcolare a parte 992

Mappa del sito
Hosted by www.Geocities.ws

1