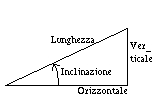
Orizzontale = Distanza cos(Inclinazione)
Verticale = Distanza sen(Inclinazione)
"cos" (coseno) e "sen" (seno) sono due funzioni trigonometriche i cui valori,
per angoli compresi fra 0 e 90 gradi, sono
riportati nella tabella alla fine di questa sezione.
E se una inclinazione e` negativa? Devi ricordarti che
cos(- Angolo) = cos(Angolo) sen(- Angolo) = - sen(Angolo)
Con queste formule si trovano le coordinate in sezione dei punti
(caposaldi), ricorsivamente.
Per esempio se abbiamo misurato
PUNTI Bussola Distanza Inclinazione 1 - 2 64 13.00 +15 2 - 3 14 7.45 +30 3 - 4 121 19.60 - 5 4 - 5 - 12.20 +90le distanze Orizzontale e Verticale fra i capisaldi in sezione sono (espresse in metri)
PUNTI Orizzontale Verticale 1 - 2 12.56 3.36 2 - 3 6.45 3.72 3 - 4 19.13 - 1.67 4 - 5 0.00 12.20
Attenzione al segno: nell'esempio la misurazione 3-4 ha Inclinazione
negativa (percio` il caposaldo 4 si trova piu` in basso rispetto
al caposaldo 3), quindi la componente Verticale e` negativa.
La componente Orizzontale e` "sempre" positiva. (Perche`?).
Da notare che quando l'inclinazione e' 90 gradi l'Orizzontale
e` zero (nell'esempio la misurazione 4-5).
Questi numeri rappresentano la posizione, in sezione,
relativa dei capisaldi, due a due.
Con questi dati si puo` valutare le posizioni dei vari capisaldi
relativamente ad uno di essi, per esempio il primo, numero 1: per il 2
non occorre fare nulla; per il 3 basta sommare la sua posizione
relativa a 2 a quella di 2 rispetto a 1.
Per il 4 si procede analogamente, stando attenti al segno!
Ecco il risultato:
. Spostamento Spostamento PUNTI Orizzontale Verticale 1 - 2 12.56 3.36 2 - 3 19.01 7.08 3 - 4 38.14 5.41 4 - 5 38.14 17.61
Quindi complessivamente siamo saliti di 17.61 metri.
La componente Orizzontale non ci dice molto; tuttalpiu` serve
per valutare quanto deve essere grande il foglio di carta millimetrata
su cui disegneremo poi la sezione.
Per sapere quanto ci siamo spostati in pianta, dobbiamo riprodurre
numericamente le operazioni che si eseguono disegnando la pianta.
A tale scopo usiamo la distanze Orizzontali e la Bussola.

Fig. 194. Nord e Est
Nord = Orizzontale cos(Bussola) Est = Orizzontale sen(Bussola) "cos" e "sen" sono le stesse funzioni trigonometriche di prima. Pero' ora c'e` un'altra complicazione: le misure della bussola vanno da 0 a 360 gradi, e nelle tabelle le funzioni sono elencate solo per angoli fra 0 e 90 gradi. Il motivo di cio` e` dovuto alle seguenti relazioni, che permettono di trovare i valori delle funzioni per tutti i gradi (se non fosse per i segni sarebbero facili da ricordare):cos( 90 + Angolo) = - sen(Angolo) cos(180 + Angolo) = - cos(Angolo) cos(270 + Angolo) = + sen(Angolo) sen( 90 + Angolo) = + cos(Angolo) sen(180 + Angolo) = - sen(Angolo) sen(270 + Angolo) = - cos(Angolo)Dunque riprendiamo il nostro esempio e calcoliamo le distanze nelle componenti Nord ed Est della pianta:PUNTI Nord Est 1 - 2 5.51 11.29 2 - 3 6.26 1.56 3 - 4 - 9.85 16.40 4 - 5 0.00 0.00Da notare che 3-4 ha una componente Nord negativa: la direzione 121-Nord indica che la galleria sta' andando verso sud-est! Ancora: 4-5 ha entrambe le componenti zero: infatti e` un pozzo, e non da` alcun spostamento in pianta.Adesso valutiamo gli spostamenti relativamente al caposaldo 1:. Spostamento Spostamento PUNTI Nord Est 1 - 2 5.51 11.29 2 - 3 11.77 12.85 3 - 4 1.89 29.25 4 - 5 1.89 29.25Finalmente possiamo dire che ci siamo spostati di poco meno di due metri verso nord, ma di quasi trenta (29,25 per l'esattezza) verso est.Tabella dei valori delle funzioni trigonometriche.Ang Sen Cos Tan Ang Sen Cos Tan 0 0.00 1.00 0.00 45 0.71 0.71 1.00 1 0.02 1.00 0.02 46 0.72 0.69 1.04 2 0.03 1.00 0.03 47 0.73 0.68 1.07 3 0.05 1.00 0.05 48 0.74 0.67 1.11 4 0.07 1.00 0.07 49 0.75 0.66 1.15 5 0.09 1.00 0.09 50 0.77 0.64 1.19 6 0.10 0.99 0.11 51 0.78 0.63 1.23 7 0.12 0.99 0.12 52 0.79 0.62 1.28 8 0.14 0.99 0.14 53 0.80 0.60 1.33 9 0.16 0.99 0.16 54 0.81 0.59 1.38 10 0.17 0.98 0.18 55 0.82 0.57 1.43 11 0.19 0.98 0.19 56 0.83 0.56 1.48 12 0.21 0.98 0.21 57 0.84 0.54 1.54 13 0.22 0.97 0.23 58 0.85 0.53 1.60 14 0.24 0.97 0.25 59 0.86 0.52 1.66 15 0.26 0.97 0.27 60 0.87 0.50 1.73 16 0.28 0.96 0.29 61 0.87 0.48 1.80 17 0.29 0.96 0.31 62 0.88 0.47 1.88 18 0.31 0.95 0.32 63 0.89 0.45 1.96 19 0.33 0.95 0.34 64 0.90 0.44 2.05 20 0.34 0.94 0.36 65 0.91 0.42 2.14 21 0.36 0.93 0.38 66 0.91 0.41 2.25 22 0.37 0.93 0.40 67 0.92 0.39 2.36 23 0.39 0.92 0.42 68 0.93 0.37 2.48 24 0.41 0.91 0.45 69 0.93 0.36 2.61 25 0.42 0.91 0.47 70 0.94 0.34 2.75 26 0.44 0.90 0.49 71 0.95 0.33 2.90 27 0.45 0.89 0.51 72 0.95 0.31 3.08 28 0.47 0.88 0.53 73 0.96 0.29 3.27 29 0.48 0.87 0.55 74 0.96 0.28 3.49 30 0.50 0.87 0.58 75 0.97 0.26 3.73 31 0.52 0.86 0.60 76 0.97 0.24 4.01 32 0.53 0.85 0.62 77 0.97 0.22 4.33 33 0.54 0.84 0.65 78 0.98 0.21 4.70 34 0.56 0.83 0.67 79 0.98 0.19 5.14 35 0.57 0.82 0.70 80 0.98 0.17 5.67 36 0.59 0.81 0.73 81 0.99 0.16 6.31 37 0.60 0.80 0.75 82 0.99 0.14 7.12 38 0.62 0.79 0.78 83 0.99 0.12 8.14 39 0.63 0.78 0.81 84 0.99 0.10 9.51 40 0.64 0.77 0.84 85 1.00 0.09 11.43 41 0.66 0.75 0.87 86 1.00 0.07 14.30 42 0.67 0.74 0.90 87 1.00 0.05 19.08 43 0.68 0.73 0.93 88 1.00 0.03 28.64 44 0.69 0.72 0.97 89 1.00 0.02 57.29 45 0.71 0.71 1.00 90 1.00 0.00 ---4.A.6 Trattazione degli anelli multipli
Il problema degli anelli chiusi nella topografia ipogea e` che quando c'e` un anello si arriva allo stesso punto seguendo due percorsi differenti, e in generale le poligonali dei due percorsi portano a due punti distinti sulla carta, ma che corrispondono allo stesso punto nella realta` [398] [399] [351] [349] .Questo e` dovuto alla presenza di errori nelle misurazioni:Una valutazione degli errori delle letture con gli strumenti [400] e` Ebussola = (1.2 + c/30)/deg , Eclinometro = (0.5 + c/40)/deg , dove c e` l'angolo di inclinazione in valore assoluto, e Ebindella = (2 + d/200) cm, dove d e` la distanza misurata in centimetri.
- la precisione con cui sono marcati i capisaldi;
- la precisione degli strumenti di misura (un centimetro per la bindella, e un grado, o mezzo, per clinometro e bussola);
- il posizionamento degli strumenti: posizione della bindella sul caposando, distanza fra lo strumento e il caposaldo durante la lettura;
- la disposizione degli strumenti: la bindella leggermente meno tesa del dovuto, o che tocca la parete, errori nel traguardo dell'altro caposaldo.
Per cui le poligonali sono affette da errori. Quando non ci sono cicli questo viene solitamente ignorato (in topografia ipogea); pero` quando ci sono anelli risulta che le poligonali non si chiudono, percio` occorre distribuire l'errore per far tornare il rilievo. Nel far cio` non si imbrogliano i dati, ma si tiene in effetti conto dell'ulteriore informazione che due punti su due pezzi di poligonale differenti devono coincidere.Il metodo dei minimi quadrati e` una procedura sofisticata e rigorosa per compensare gli errori in anelli non affetti da sviste. Esso permette di trovare la posizione statisticamente piu` significativa quando ci sono piu` percorsi che portano allo stesso punto e consiste nel scegliere il valore che minimizza l'errore quadratico medio delle misure. Prima di passare ad esaminarlo nei dettagli notiamo che esso e` sovente superfluo viste le accuratezze che solitamente si ottengono nei rilievi di grotta. Tra parentesi certi errori sistematici sono irrilevanti alla non-chiusura di anelli poiche` ne modificano solo la disposizione spaziale; per esempio un errore sistematico sulle direzioni ruota l'anello, mentre uno sulle distanze lo espande o rimpicciolisce. Per l'inclinazione un errore sistematico produce in genere una non-chiusura.Il metodo dei minimi quadrati e` molto semplificato nel rilievo ipogeo, poiche` in genere tali rilievi contengono solo traversamenti e non triangolazioni ne` trilaterizzazioni. Percio` la matrice che esprime la geometria e` molto semplificata e contiene, in genere, solo due elementi non nulli per ogni riga, e precisamente con valori +1 e -1.Una distribuzione degli errori, simile alla compensazione nella chiusura dei cicli, si ha quando per piu` di un caposaldo del rilievo sono note le coordinate GPS (per esempio una cavita` con piu` ingressi), e si vuole localizzare la grotta sulla carta. In tal caso bisogna tener conto dell'errore nelle tratte di rilievo e di quello dei dati GPS [401] . Anche in questo caso si puo` utilizzare il metodo dei minimi quadrati per distribuire l'errore. Se Xi sono le posizioni (da trovare) dei capisaldi e xi sono quelle date dal GPS, mentre lij e` la lunghezza del rilievo fra i capisaldi, l'errore quadratico e`E = ∑wi (Xi - xi)2 + ∑vij (Xi - Xj - lij)2dove la prima somma e` sui capisaldi, e la seconda sui rilievi che li congiungono. wi e vij sono dei pesi, che dovrebbero essere proporzionali all'inverso delle incertezze delle misure.4.A.6.1 La media pesata
La media pesata e` una procedura per stabilire che valore assegnare ad una certa quantita` avendo a disposizione piu` misurazioni di essa, ognuna con un certo grado di precisione [402] . Nel caso di un anello chiuso, che coordinate assegnare al punto finale avendo due poligonali che lo raggiungono.La covarianza e` l'espressione numerica del grado di precisione quando la quantita` e` un vettore X. Nel caso ad una componente (un solo numero) la covarianza si riduce alla varianza, che e` pari al quadrato della deviazione standard. Il peso associato ad una misura e` l'inverso della covarianza:W = C-1Date n misure di X, X1, ..., Xn, con covarianze C1, ..., Cn, e pesi Wk espressi come sopra, il valore di X che minimizza l'errore quadratico medio,E = (X1 - X)2 + ... + (Xn - X)2risulta la media ponderata:X = ( W1 + ... + Wn )/sup{-1} ( W1 X1 + ... + Wn Xn )Un traversamento (senza giunzioni) si comporta come una singola misuraX = X1 + ... + Xncon covarianza (supponendo le misure indipendenti)C = C1 + ... + CnLa soluzione del problema dei minimi quadrati e` dunque una media pesata.4.A.6.2 Distribuzione proporzionale
Si tratta di distribuire una certa quantita` D in n gruppi, ognuno con una capacita` mk Questo serve per distribuire l'errore fra le varie tratte che compongono un ramo di poligonale. La soluzione e` simile alla media pesata: il gruppo k riceva una parteDk = ( m1 + ... + mn )-1 mk D4.A.6.3 Linearizzazione
I dati sono misurati con coordinate distanza D, azimuth A, e inclinazione I. Quando sono resi sulla carta si trasformano in coordinate ortogonali (est X, nord Y, e quota Z)X = D cos( I ) sin ( A )
Y = D cos( I ) cos ( A )
Z = D sin( I )Questa trasformazione non e` lineare. Invece il metodo di aggiornamento dei minimi quadrati presuppone un probelma lineare. Questo significa che se i dati non sono vicini al problema originale la soluzione puo` essere molto diversa dalla posizione reale.Conoscendo gli errori su D, A ed I si possono valutare quelli di X, Y e Z. Le covarianze nei due sistemi di coordinate misure sono legate dallo Jacobiano, J = d(X,Y,Z) / d(D,A,I) della trasformazione:CXYZ = J CDAI JtLo Jacobiano risulta (questa espressione presuppone gli angoli espressi in radianti)
cos(I) sin(A) D cos(I) cos(A) - D sin(I) sin(A) cos(I) cos(A) - D cos(I) sin(A) - D sin(I) cos(A) sin(I) 0 D cos(I) Tuuto cio` e` importante perche` quando calcolo la covarianza di un pezzo di poligonale posso sommare le covarianze delle singole tratte se queste sono espresse in un sistema ortogonale.Da notare che lo Jacobiano diventa singolare quando l'inclinazione e` verticale (+/- 90°). Infatti in tal caso l'azimuth risulta indeterminato. Ne segue che in tal caso si hanno matrici di covarianza singolari. l'errore in Z e` pari a quello sulla distanza, mentre gli errori in X e Y restano incerti (anche se proporzionali a D e all'errore su I) poiche` A e` indefinito. Mediando sui valori dell'azimuth possimao usare la covarianzaCXYZ = diag( D2 dI2 / 2, D2 dI2 / 2, dD2 )Uno dei problemi nella trattazione automatica dei cicli [403] e` la determinazione dell'insieme dei cicli fondamentali [404] , cioe` del minimo insieme di cicli indipendenti. Questo insieme puo` essere scelto in molti modi differenti, e matematicamente equivalenti. Tuttavia, dal punto di vista del rilievo ipogeo i cicli fondamentali dovrebbero avere due carattersitiche:perche` questo rende piu` probabile la detezione di sviste. Inoltre quando viene rilevato un errore in un ciclo corto e` piu` facile da ritopografare in grotta. La determinazione dell'insieme ottimale di cicli fondamentali, richiede l'analisi di tutte le combinazioni, e percio` non e` fattibile (in un tempo ragionevole), se non per grotte semplici. Invece si determina un insieme subottimale, con opportune strategie di ricerca, che non richiedono troppo tempo anche per sistemi complessi.
- avere il minor numero di tratte,
- avere la minima sovrapposizione fra ogni due cicli
Supponiamo di avere N cicli fondamentali, contenenti K+1 punti (capisaldi). I punti indipendenti sono K dato che uno di essi puo` essere arbitrariamente posizionato. Esiste una relazione (di Eulero) fra il numero di cicli, il numero di punti e il munero T di tratte (supponendo che ogni punto appartenga a due o a tre tratte):T = K + NL'impostazione del sistema di equazioni non e` complicata, ma solo laboriosa. Esso si riduce alla formaMij Xj = ∑in Wk Tk - ∑out Wk Tkdove la prima somma e` estesa a tutte le tratte entranti nel punto Xj, e la seconda e` estesa alle tratte uscenti da esso. Il coefficiente Mjj e` la somma dei pesi delle tratte entranti ed uscenti da Xj. Quando gli indici sono differenti il coefficiente Mij e` pari a -Wk, l'opposto del peso della tratta che collega il punto Xi al punto Xj, ed e` nullo se i due punti non sono direttamente collegati.
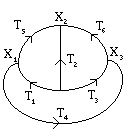
Fig. 195. Anelli multipli
A titolo di esempio consideriamo la situazione in figura a destra. L'errore quadratico e`E = W1 (T1 - X1)2 + W2 (T2 - X2)2 + W3 (T3 - X3)2 + W4 (T4 + X1 - X3)2 + W5 (T5 + X1 - X2)2 + W6 (T6 + X3 - X2)2
Quindi il sistema diventa| W1+W5+W4 - W5 - W4 | | X1 | | W1 T1 - W4 T4 - W5 T5 | | - W5 W2+W5+W6 - W6 | | X2 | = | W2 T2 + W6 T6 + W5 T5 | | - W4 - W6 W3+W4+W6 | | X3 | | W3 T3 + W4 T4 - W6 T6 |4.A.6.4 Determinazione e correzione di sviste
Il metodo dei minimi quadrati stima le correzioni delle singole misure in base ai loro pesi (che sono stimati o calcolati a partire dalle precisioni delle misure). Se la discrepanza di chiusura di un anello eccede la precizione delle misurazioni (cioe` l'errore statistico) allora c'e` un errore macroscopico nei dati: nella lettura degli strumenti, o nella scrittura dei valori, o nel collegare piu` rilievi. In tal caso si dovrebbe rifare il rilievo. In alternativa si puo` cercare di trovare qual e` il dato affetto da errore macroscopico e modificarlo in modo da chiudere il ciclo.
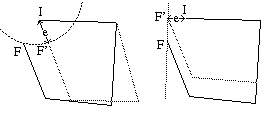
Fig. 196. Correzione sviste
La detezione degli errori grossolani cioe` delle sviste e la loro correzione e` possibile in fase di restituzione del rilievo qualora l'errore grossolano coinvolge un tiro di un ciclo chiuso [405] [406] [407] .Certe sviste hanno una caratteristica distintiva, che permette di riconoscerne il tipo. Per esempio un errore di direzione non ha effetti sulla chiusura del ciclo in sezione. Percio` se il ciclo non si chiude solo in pianta, si dovrebbe cercare l'errore fra le misure di direzione.L'idea per correggere un errore grossolano consiste nel provare ad aggiustare una alla volte tutte le misure delle tratte che compongono il ciclo, per vedere se ce n'e` una il cui aggiustamento permette di chiudere il ciclo tenendo in conto l'accuratezza delle misure. Il problema e` come effettuare gli aggiustamenti e avere un criterio di qualita` degli stessi.Per la direzione variando un angolo il punto finale del ciclo descrive un arco di circonferenza. Si prende come aggiustamento della direzione l'angolo per cui il punto finale e` piu` vicino al punto iniziale del ciclo. La loro distanza e` utilizzata come criterio di qualita` dell'aggiustamento (Figura a sinistra).Per le distanze, variando una distanza il punto finale descrive una retta. Nuovamente si prende come aggiustamento la distanza per cui il punto finale e` piu` vicino al punto iniziale, e la loro distanza ne rappresenta la qualita`. La complicazione e` che si deve lavorare in 3 dimensioni anziche` nel piano (Figura a destra).Per le inclinazioni la situazione e` come per le direzioni, ma anche qui occorre lavorare in 3 dimensioni.Alla fine dopo aver provato con tutte le misure, se ne risulta una sola per il cui aggiustamento la distanza fra punto finale e punto iniziale rientra nei limiti di accuratezza del rilievo, questa e` la svista e l'aggiustamento ne rappresenta il valore corretto.Questo metodo ha dei limiti. Primo fra tutti l'errore del rilievo: se questo non e` piccolo risulta incerto dire quale sia la svista perche` ci saranno piu` punti il cui aggiustamento rientra nei limiti dell'errore di rilievo. Inoltre puo` accadere che ci siano davvero, in particolari situazioni, due aggiustamenti "equivalenti" e quindi non sia possibile stabilire quale sia l'errore grossolano. In questo caso avere piu` cicli potrebbe essere d'aiuto. Infine in caso di piu` errori grossolani in un solo ciclo la loro presenza potrebbe essere rilevata dalla impossibilita` di chiudere il ciclo con un singolo aggiustamento, pero` la correzzione risulta piu` complessa. E` un problema di segnale/rumore: il rumore e` l'errore intrinseco di rilievo, il segnale sono gli erroro grossolani visti come gli aggiustamenti necessari a chiudere il rilievo. Se il rumore e` troppo alto (errore troppo elevato) risulta difficile "sentire" il segnale, cioe` trovare l'aggiustamento o gli aggiustamenti da fare. Se il rumore e` molto basso, si puo` arrivare a corregere anche due o piu` errori grossolani.Si dovrebbe anche tener conto di quali sono le piu` probabili cause di sviste (alcune di queste dipendono dalla lingua)
- confondere '6' con '7';
- sbagliare scala sul clinometro;
- sbagliare la lettura dei metri, in misure corte, poiche` sbiaditi sul nastro;
- sbagliare direzione, a causa del verso, per esempio 154 invece di 146;
- sbagliare segno nella inclinazione, per esempio -3 invece di +3.
La distribuzione statistica degli errori di chiusura dei cicli chiusi mostra una prima parte decrescente velocemente, seguita da una lunga coda. La coda e` dovuta agli errori grossolani e l'analisi della prima parte della curva fornisce una indicazione della accuratezza [408] . Una valutazione degli errori delle letture con gli strumenti [400] e` Ebussola = (1.2 + c/30)/deg , Eclinometro = (0.5 + c/40)/deg , dove c e` l'angolo di inclinazione in valore assoluto, e Ebindella = (2 + d/200) cm, dove d e` la distanza misurata in centimetri. del rilievo (cioe` degli strumenti e del loro utilizzo) [406] .Per ogni ciclo di N tratte e con lunghezza totale L, e con errore di chiusura (dx,dy,dz) si possono calcolare i seguenti stimatori [409]
- errore angolare orizzontale, arctan( [dx2 + dy2]1/2 / L )
- errore angolare verticale, arctan( dz / L ). Questo e` equivalente ad un errore di calibrazione del clinometro se si facessero letture in un sol verso.
- errore angolare totale, arctan( [dx2 + dy2 + dz2]1/2 / L ). Questo e` una combinazione dei due precedenti.
- errore medio, [dx2 + dy2 + dz2]1/2 / N. Questa e` una media; in pratica la tratta piu` lunga risulta circa tre volte la lunghezza media delle tratte, percio` l'errore della tratta piu` lunga e` circa tre volte questo valore.
4.A.7 Valutazione dell'anomalia locale
Avendo a disposizione misure in eccesso (cioe` sia dal caposaldo A al caposaldo B, che viceversa) e` possibile correggere le misure degli azimuth compensando l'anomalia magnetica locale, a meno di una costante (anomalia media globale). Se il rilievo e` fatto con letture doppie (in entrambe le direzioni) si possono utilizzare cicli chiusi per determinare errori grossolani (poiche` quando si considerano cicli le anomalie locali si cancellano) [410] .
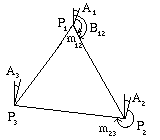
Fig. 197. Anomalia magnetica
Per esempio consideriamo un triangolo con vertici P1, P2, e P3. Supponiamo che le anomalie (incognite) nei tre punti siano A1, A2, e A3. Pertanto, per esempio, se da P1 a P2 misuriamo m12 l'angolo effettivo con nord magnetico e` b12 = m12 + A1.L'angolo P2P3P1 vale allorab32 - b31 = m32 - m31Utilizzando il fatto che bij-bji= +/- 180°si ottiene un sistema di tre equazioni in tre incognite. Pero` questa tre equazioni non sono indipendenti, essendo la loro somma una relazione che deve sussistere fra le misure.La valutazione delle somme degli angoli interni dei triangoli permette di rilevare macroscopici errori di lettura dei dati (nell'ipotesi di avere misurazioni sufficientemente ridondanti). Vedi P.R.Wolf e C.D.Ghilani "Adjustment Computations, Statistics and Least Squares in Surveing and GIS", Wiley 1997.E` possibile quindi trovare la differenza fra anomalie locali in due punti a partire da queste equazioni.
marco corvi - Thu May 29 15:25:39 2008
Prev Up Top Next Contents
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 2.0 Italy License.