Prev Up Top Next Contents
3.C Fisica degli armi
3.C.1 Fisica della tirolese
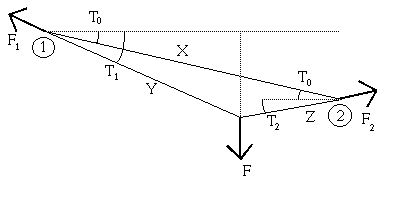
Fig. 153. Tirolese: diagramma delle forze
Sia
L la distanze fra i due armi tra cui e` tesa la corda e
T0 l'angolo che forma con l'orizzontale
[
302] [
218] [
321] [
249] .
Le considerazioni che seguono sono approssimate, poiche` non
tengono conto del peso della corda e della sua elasticita`.
Una corda tesa fra due punti si disporrebbe come
una curva detta "catenaria", y = a [Ch(x/a) - 1], se non fosse
estendibile, cioe` se non variasse il "peso al metro" a causa
della elasticita`. Vedi [
322] per maggiori dettagli.
Con uno speleologo appeso ad un punto a distanza
X dall'armo
di sinistra (misurato lungo la corda quando e` libera), le
equazioni dell'equilibrio statico sono
- F1 sin(T1) + F2 sin(T2) = F
- F1 cos(T1) = F2 cos(T2)
- F X cos(T0) =
F2 L sin(T2) cos(T0)
+ F2 cos(T2) L sin(T0)
dove
F e` la forza (verso il basso) dovuta al peso dello speleologo.
Aggiungendo le condizioni sulla tensione della corda (
E e` il
coefficiente di elasticita` della corda),
- Y cos(T1) = X cos(T0)
- Z cos(T2) = (L-X) cos(T0)
- Y = Yo E F1
- Z = Zo E F2
- Yo + Zo = Lo
per cui si ha
(9) Y/F1 + Z/F2 = L/T
dove
T e` la tensione della corda (senza lo speleologo appeso).
Lavorando sulla equazione (9), usando la (4) e la (2), si ottengono
- F1 = T cos(T0)/cos(T1)
- F2 = T cos(T0)/cos(T2)
e con la (1),
(12) F = T cos(T0) [ tan(T1) + tan(T2) ]
La (3) fornisce una relazione fra
Ti e
Fi.
Da queste si ricavano
- tan(T1) = F/T (L-X)/L 1/cos(T0) + tan(T0)
- tan(T2) = F/T X/L 1/cos(T0) + tan(T0)
Finalmente possiamo scrivere l'espressione delle forze che agiscono sugli
armi in funzione delle variabili note (distanza fra gli armi
L,
e dislivello
T0, tensione della corda
T,
peso dello speleologo
F, e sua posizione
X),
- F1 =
( T2 + 2 T F (L-X)/L sin(T0) + F2 {(L-X)/L}2
)1/2
- F2 =
( T2 - 2 T F X/L sin(T0) + F2 {X/L}2 )1/2
Da queste si vede che in ogni caso
(17) Fi <T + F
Tuttavia la teleferica e` efficace se l'angolo che si forma, quando lo
speleologo si appende non e` troppo grande, cioe` se non diventa un scendere
e risalire da un pozzo. Dunque valutiamo anche la condizione per cui
la corda resta "abbastanza tesa".
Con un poco di altra algebra si trova
(18) sin(T1) =
( 1 + cos2(T0) / { sin(T0) + F/T (L-X)/L }2
)-1/2
da questa relazione si vede che affinche` l'angolo formato dalla corda
sotto il peso dello speleologo sia inferiore ad un valore fissato piccolo,
eps, e` necessario che
(19) T >F / (2 eps)
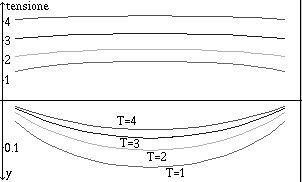
Fig. 154. Tirolese: tensione e abbassamento
In pratica se vogliamo un angolo non superiore a 10 gradi, la tensione
dovra` essere quasi tre volte il peso dello speleologo, quindi gli
armi dovranno sostenere una forza pari a quattro volte il peso dello
speleologo. In figura sono riportate la tensione della corda e
l'abbasamento del punto cui e` appeso lo speleologo, per quattro diversi
valori della tensione della corda libera, espressi come multipli
del peso dello speleologo.
Da prove pratiche la tensione sugli ancoraggi, durante il tensionamento
arriva a 600 daN. Dopo si hanno tensioni di 120 - 200 daN.
Quando lo speleologo si appende questa cresce del 80 - 120
Queste considerazioni si applicano anche agli armi ad 'Y',
cioe` agli armi doppi con un coniglio, o un anello di cordino
ripartitore di carico.
Anche gli ancoraggi dei traversi sono degli armi a 'Y', tanto piu`
tirati quanto piu` la corda e` tesa. Per questo motivo
le partenze dei traversi devono sempre avere un armo doppio,
ed e` meglio passare i traversi appesi alla corda, piuttosto che
caderci sopra, sollecitando maggiormente gli ancoraggi.
3.C.2 Stima della profondita` di un pozzo
Se il pozzo e` semplice e si vede il fondo si puo` stimarne (o
misurarne) la profondita` con un distanziometro [
256] .
Tuttavia questo metodo ha problemi se il pozzo e` articolato
e presenta terrazzi. Pertanto da` solo un valore minimo della
profondita`.
Il lancio di una pietra (non troppo piatta) e` utile per valutare
la profondita` di un pozzo. Il tipo di caduta della pietra serve anche
per una valutazione approssimativa della morfologia del pozzo.
Nella
Sez. 4.1
e` stata riportata la formula approssimata
valida per stimare la profondita` dei pozzi compresi tra 25 e 100 metri,
P [metri] = 25 t [s] - 40
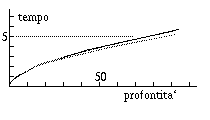
Fig. 155. Pozzi: stima dell profondita'
La velocita` di caduta del sasso cresce per l'accelerazione di gravita`
g
ma e` contrastata dal frenaggio dovuto all'aria, che e` proporzionale
alla velocita` stessa: - a v.
Per la legge di Stokes il coefficiente a e` proporzionale
alla viscosita` dell'aria (circa u =
2x10-5 N/s m2)
e a caratteristiche geometriche del corpo in caduta.
Per una stima qualitativa possiamo prendere il valore teorico per un
oggetto sferico (6 πR, dove R e` il raggio).
Quindi a risulta (dobbiamo dividere per la massa del sasso, dato
che consideriamo accelerazioni invece di forze)
6 πR u / (4/3 πR3 d), che a conti fatti
e` dell'ordine di 0.1, per un sasso di 5 cm di diametro.
Un valore accettabile e` a=0.25 Hz.
Ne risulta che lo spazio di caduta e`
x = (g/a) (t - (1-e- a t)/a )
dove t e` il tempo di caduta (v. figura, linea tratteggiata).
Al tempo di caduta t bisognerebbe aggiungere quello che il suono
impiega a ritornare t' = x/vs, ma questo e` una frazione
di secondo (la velocita` del suono e` circa 331 m/s a 1 atm e 0°C),
e puo` essere trascurato in una valutazione
approssimativa. In figura la linea continua tiene conto anche del
ritardo di ritorno del suono.
3.C.3 Fisica dell'armo doppio
In un armo doppio (cioe` a "Y") l'angolo fra le due gasse deve
essere inferiore ai due angoli che la corda forma con esse
[
323] [
324] [
249] .
In questa condizione la forza su ognuno dei due punti d'ancoraggio
e` inferiore alla tensione della corda.
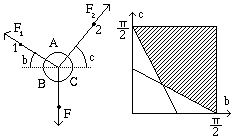
Fig. 156. Armo a Y: diagramma delle forze
Dal diagramma delle forza (v. figura a sinistra) la forza sull'ancoraggio
numero "1" risulta
F1 = ( F / cos(b) ) 1/(tan(b) + tan(c))
Se imponiamo che questa sia inferiore a
F si ha che deve
essere
b >π/ 2 - 2 c
Similmente considerando la forza sull'ancoraggio numero "2" deve
essere
c >π/ 2 - 2
b.
Queste due condizioni corrispondono all'area tratteggiata nel
diagramma a destra).
E` facile vedere che queste due condizioni sono equivalenti a dire che
l'angolo
A e` inferiore sia a
B che a
C.
3.C.4 Ripartitore di carico
Il ripartitore di carico dispone il punto di attacco della forza
lungo una ellisse con i fuochi nei punti di ancoraggio; questa e`
la figura geometrica descritta dal vertice del triangolo tale che
la somma dei lati V1 e V2 sia costante.
Il vertice del triangolo si dispone in modo che la direzione di trazione
sia perpendicolare alla tangente all'ellisse in tale punto.
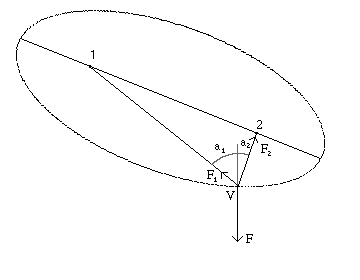
Fig. 157. Forze in un ripartitore di carico
In tale configurazione, la direzione di trazione risulta bisettrice
dell'angolo al vertice, quindi la forza si distribuisce in maniera
uguale sui due ancoraggi.
La forza sugli ancoraggi dipende dal rapporto della lunghezza dell'anello
del ripartitore e dalla distanza fra i due ancoraggi.
Essa varia quindi con l'angolo al vertice, come in un ancoraggio doppio
ben regolato. Quest'angolo varia con la direzione di trazione.
Esso e` massimo quando questa e` perpendicolare alla direzione fra i due ancoraggi,
situazione in cui la forza sugli ancoraggi e` massima.
Quando la direzione di trazione e` parallela alla linea di congiunzione degli
ancoraggi, la trazione si distribuisce a meta` su ciuscuno di essi.
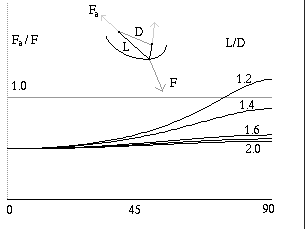
Fig. 158. Forze in un ripartitore di carico
marco corvi - Sat Sep 13 13:44:32 2008
Prev Up Top Next Contents
This work is licensed under a Creative Commons
Attribution-NonCommercial-ShareAlike 2.0 Italy License.





