The 3-plane Array

As stated earlier, the room in which you are sitting right now can be thought of as a 3-dimensional plane of empty space (or rather, a 'hollow cube') roughly 10 feet high, wide, and deep. As part of the "thought experiment" mentioned earlier you can imagine your room to be a central plane in an array of 3-planes / hollow cubes / 3-dimensional rooms. Once this notion is presented, however, there lies the question of precisely "where", in relation to your own 3-plane, the rest of the 3-planes of the array lie. Take note, if you will, that this is not the first time we've encountered this question: there was, earlier in the material, the situation in which we proposed to 'explain' to a Linelander / Flatlander, confined to a single, central plane of his 'room array', just "where", in relation to his own plane, the rest of the planes of the array were to be found. In both cases, the 'answer' agreed upon was that all of the other planes of the array occupied the "same space" as his own plane, because there was no means as of the subject's dimension to express the spatial separateness of surrounding planes from his own plane. It was quite apparent, however, that, in physical reality, all of the planes of the array were quite separate, each extending outward from his plane and possessing its own unique position within the array. But in terms of what the subject could comprehend, all we could say was that all of the planes of the array occupied the "same space". Does this answer our question as to "where", in relation to our own 3-plane, the rest of the 3-planes of the array lie? That is, can we apply this "same space" reasoning to the 3-plane array? Or perhaps the question to ask is if there's any reason that this reasoning shouldn't be true for the 3-plane array? That is to say, this reasoning is the product of pure analogy - perhaps the most important tool of spatial visualization - and in a sense, it's impossible for analogy to be wrong. What, then, would this reasoning tell us about an array of 3-planes?

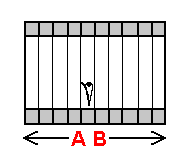
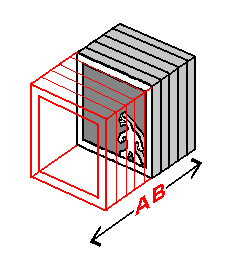
What can we rely upon to confirm the unusual concept of a 3-dimensional plane occupying the "same space" as another 3-dimensional plane? What evidence, furthermore, is there that exists that proves that what we are calling a '3-plane' actually exists? The concept most closely related to this topic lies in the mental construct called the tesseract. What is a tesseract? A tesseract is a 'cube within a cube'. The inner cube is smallest. Physically, the inner and outer cubes are of equal size. The inner cube appears to us to be smaller, however, because it is diminished by the effects of 4-dimensional perspective. Because we cannot directly comprehend this 4-dimensional perspective, our best reference as to the 4-dimensional distance of the inner cube from where we are is by it perceived size: the smaller the inner cube, the farther away we are to assume it lies. We are now to apply this logic to an array of 3-planes: though 3-planes occupy the same 3-dimensional space as the cubes of a tesseract do, we can refer to the distances of these 3-planes from our own 3-plane, if desired, by designating a specific size to each of them - a size directly related to the 3-plane's distance from us. Let this provide us with a powerful tool that can be considered to be our best means of determining 4-dimensional distance within a 3-plane array.

Our experience of a 3-plane array would be equivalent to the Linelander's and Flatlander's experience of the array of planes within which they dwell. Being on a central plane, you are surrounded on 2 "sides" by 3-planes that you can at best say occupy the "same space" as your own 3-plane. You are unable to detect these "sides" in that the directions in which these "sides" lie, are directions that extend perpendicular to the very dimension to which your 3-plane / 3-room belongs. It is out from your own 3-plane and into these opposite directions that the 3-planes surrounding your own 3-plane 'accumulate' and extend outward. Regardless of your inability to comprehend how the surrounding 3-planes of the array are spatially separate from your own 3-plane, each 3-plane possesses its own unique position along an array arranged in a linear fashion. If desired, imagine 3-planes of greater distance away to appear smaller, as with a tesseract.

It was shown earlier that, when planes of 'empty space' were 'lined up', they could be considered to "combine", so to speak, into a 'single entity', forming a 'higher space': the '1-room array', if you recall, forms 2-space; and the '2-room array', 3-space. Afterward, we found that though we could experience these rooms / planes "all at once", a subject confined to a single room / plane of the structure was capable of experiencing only the room / plane that he inhabited. That individual plane, by itself, could seem almost like nothing compared to the 'higher space' formed by all of the rooms / planes when "combined" together 'as a whole'. Is it at all possible, however, that the subject, though confined to his single plane, would be able to conceive of this 'higher space' formed by experiencing that entire array of rooms / planes "all at once"? This, by all means, can be done - the medium of the stack-diagram, take note, makes such a feat possible.

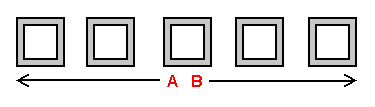
The subject, say, a Flatlander, first acknowledges that the array of rooms / planes within which he dwells is in fact linear - and that the planes surrounding his own plane, though said to occupy the "same space" as of his own dimension, are in some way spatially separate. The top stack-diagram on the left embodies a Flatlander's conception of 3-space. With this stack-diagram in mind, the Flatlander's basic understanding would be that 3-space could be defined as 'the empty space formed by a group of empty 2-planes experienced simultaneously'. That is, in order to experience 3-space, you must experience more than one 2-plane at once - which a Flatlander can't do. So even though a Flatlander can't experience 3-space "as it is" like we can, he can at least conceive of the concept of multiple 2-planes being experienced simultaneously. The same concepts would hold true for a Linelander and 2-space. In fact, a Linelander's conception of 2-space is included on the left also. A Linelander would define 2-space as 'the empty space formed by a group of empty 1-planes experienced simultaneously'. Though the Linelander can't experience more than one 1-plane at once, he can at least conceive of the concept of multiple 1-planes being experienced simultaneously.

Now, consider yourself to be the subject 'added to a central plane of the array' (just as in an earlier section we added lower-dimensional subjects onto the central plane of an unoccupied array of planes). In considering yourself as being on the central 3-plane in an array of 3-planes, you are in doing so assuming everything true for these lower-dimensional subjects to be equally true for your own situation. Allow this concept to establish itself in your field of understanding. Given the means of reasoning just described, you can experience only one 3-plane of the array you are contained within at any given time: the one that you are inhabiting. You are 'unaware' of the 3-planes surrounding your own 3-plane (that supposedly occupy the "same space") in the same way that the Linelander and Flatlander were 'unaware' of the planes surrounding them. How do we conceive of the 'higher space' formed by a 3-plane array (that is, 4-space)? By means of a stack-diagram.

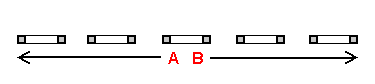
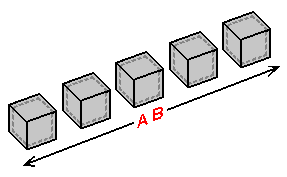Just as 2-space can be defined as 'multiple 1-planes experienced simultaneously', and 3-space can be defined as 'multiple 2-planes experienced simultaneously', we can define 4-space as 'multiple 3-planes experienced simultaneously' - something that we are not capable of doing. Displayed on the left, then, is 4-space as we would conceive of it - in the form of a stack-diagram. (The 'dotted line' seen just within the outer border of each cube signifies that the cubes are hollow). 4-space would be formed by all of the 3-planes "combining" into a single 'empty space' - in the same way that planes "combined" together earlier to form '2-space' and '3-space'. Though all of the 3-planes shown supposedly occupy the "same space", 4-dimensional distance from the 3-plane of origin is to be pictured by imagining those distant planes to be diminished in size, acted upon accordingly by perspective, in the same way the inner cube of a tesseract is acted upon by perspective.

"Of what use", you may ask, "would we have of such an 'array of 3-planes'?" Follow, if you will, the following reasoning:

A square is a 2-dimensional object that could be said, as stated earlier, to be an array of segments. Segments are 1-dimensional objects, and each segment, in 'lining up' to form a square, takes up a single 1-plane. The square, as a result, exists simultaneously across multiple 1-planes. A square, therefore, is a 2-dimensional object made up of 1-dimensional objects.

A cube is a 3-dimensional object that could be said, as stated earlier, to be an array of squares. Squares are 2-dimensional objects, and each square, in 'lining up' to form a cube, takes up a single 2-plane. The cube, as a result, exists simultaneously across multiple 2-planes. A cube, therefore, is a 3-dimensional object made up of 2-dimensional objects.

With those facts in mind, we can conclude that a 4-dimensional object could be said to be made up of an array of 3-dimensional objects, each 3-dimensional object assigned to its own 3-plane. The 4-dimensional object, as a result, exists simultaneously across multiple 3-planes. We will see this later on in the material when the hypercube is constructed.

As of now, we will go about studying something that in a manner of speaking could be considered a '4-dimensional object' in that it exists simultaneously across multiple 3-planes: a line extended perpendicular to an array of 3-planes.