A Line Across the 3-plane Array

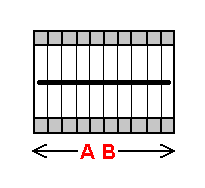
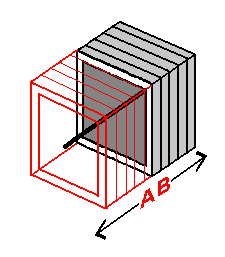
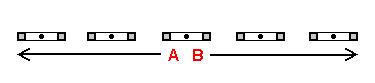
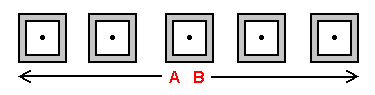
Displayed on the left are representations of a line extended perpendicular to the 1-plane array and 2-plane array we are familiar with.

Once again directly below, we see the same representations, modified to suit our needs. By observing the illustrations on the left, you will find that every plane within both arrays is intersected by the line at a point (in the plane's spatial center). The illustrations below emphasize this concept by dividing the line into the distinct cross-sections at which the intersections occur.

Given each subject, and the line that lies perpendicular to the array of rooms / planes in which he lies, assume that we have the task of 'explaining' to each subject the "location" of the line that extends perpendicular to his plane. What would we tell them? After thinking about it for a while, I feel that the best answer would be: "the line that extends perpendicular to your room exists inside of the point that lies in the center of your room". This is accurate in that it's an explanation that the Linelander / Flatlander can understand: as of their own dimension, there's simply no way to "express" the directions that the line extends into, in relation to the point at which their room is intersected.

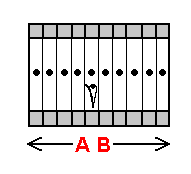
Unlike a Linelander / Flatlander, we are quite familiar with the lines extended perpendicular to the first and second dimension portayed above. Displayed directly below are representations of these lines in stack-diagram form (as a Linelander / Flatlander would conceive of the line).

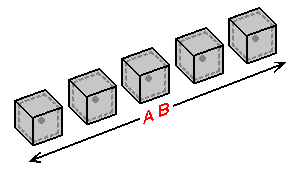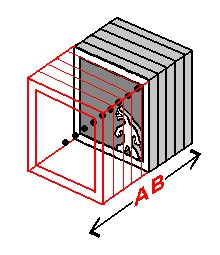
How, then, do we visualize a line extended perpendicular to the third dimension? Presented to the left is such a line. If a line perpendicular to our own dimension intersected your room (the central 3-plane in an array of 3-planes) in the same way that the plane of the Linelander / Flatlander was intersected, your room would have been intersected at a point - a distinct point that lies up above the floor, in your room's spatial center (as with the rooms of the Linelander and Flatlander). After examining the stack-diagrams of the lines extended perpendicular to the first and second dimension presented above, we can conclude that 3-planes surrounding your 3-plane would be intersected in the same manner - at a point in their spatial center. It is in lining up the 3-planes in the stack-diagram so that they share the "same space", we can see that all of the cross-sections of the line share the same 3-dimensional location.

"Where" is this line? This is a difficult question. The best answer to this question exists in the form of the explanation we gave the Linelander and Flatlander concerning the "location" of a line perpendicular to their own dimension: "the line that extends perpendicular to your room exists inside of the point that lies in the center of your room". Our best conception as to the "location" of a line extended perpendicular to the third dimension is that it would be "inside" the cross-section of the line as observed from any of the 3-planes the line passes through. This description is accurate in that it's an explanation that we can understand: as of our own dimension, there's simply no way to "express" the directions that the line extends into, in relation to the point at which the room of the observer is intersected. This line, take note, extends outward in ways that we have never encountered, that no 3-dimensional 'means of reasoning' can describe. Because we can't directly visualize the 4-dimensional extension of a line extended perpendicular to the third dimension, our best means of working with it is by means of a stack-diagram.

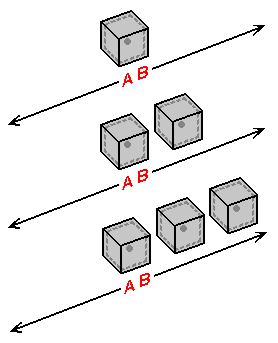The stack-diagrams in the illustration to the right represent our best means of visualizing 4-dimensional extension. In the top stack-diagram we see the central 3-plane in the middle of where an array of 3-planes would be. This 3-plane holds the initial cross-section of the line extending perpendicular to the third dimension that we will begin to visualize right now. To extend the line, we decide which direction - direction 'A' or direction 'B' - the line will be extended into. We will choose direction 'B'. We visualize the extension of the line 'one 3-plane at a time' by constantly 'adding' the new cross-sections produced by the extension of the line, onto the line as it has been extended so far. This is demonstrated to the right by means of the stack-diagrams on the right that follow the first one. The extension that occurs in the stack-diagram directly represents the extension perpendicular to the 3-planes that occurs in physical reality.

The first step toward understanding the extension of the line here is to be aware that the extension of the line into a new 3-plane is in essence a change in the fourth spatial coordinate of the tip of the extending line. By mentally 'documenting' the transfer of the tip of the line from the spatial center of one 3-plane to another, a sort of "mental incrementation" can be performed. As this "mental incrementation" takes place, the tip of the line is to be considered to become more 4-dimensionally distant from the 3-plane from which the extension started. The more 3-planes the line extends through, the 'longer' the tip of the line could be considered to become. Let this inform us as to the precise nature of how an array of planes intersected at a right angle by a line would relate to that line. In the next section, we bring together all of the knowledge accumulated up to now to form a representation of 4-space beyond anything presented so far.