The Polyominoids
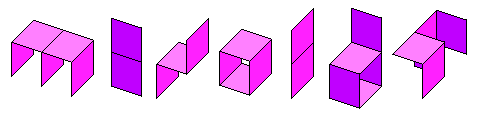
The Minoids inside the cubic lattice
|
 |
||||||||||||||||||||
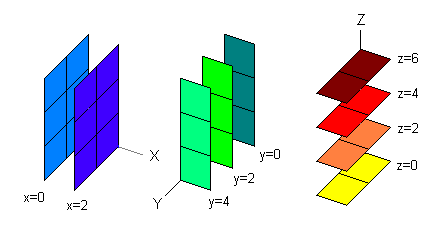
Boxes
0 <= x <= 2a
0 <= y <= 2b
0 <= z <= 2c
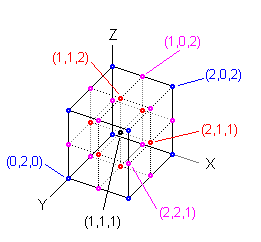
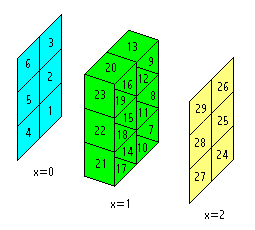
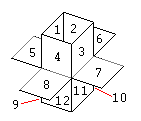
The numbering convention is such that permits to have an incrementing pattern based in signification, being the x coordinate, the first of all dimensions, the Most Significant Coordinate. In the figure first minoid, the number 1, has coordinates (0, 1, 1), minoid 2 has coordinates (0, 1, 3) and so on. The last minoid, the 29, has coordinates (2, 3, 5).
Minoids bounded by a Box
a + b + c - 1 = 5
The maximum order is simply the total number of minoids of the box. For the Box(1,2,3) the maximum order is:ab(c+1) + a(b+1)c + (a+1)bc = 29
This minimum and maximum orders of the Box(1,2,3) indicates this box is the bounding box for some of the 5, 6, 7, ... , 28, 29-minoids. Both, the cyan and yellow sections (x=0, x=2) of the Box must have at least 0 minoids and at most b*c = 6 minoids. The green section (x=1) of the Box(1,2,3) must have at least 1 minoid and at most b(c+1) + (b+1)c = 17 minoids.
|
These are all the translations' boxes for bounding all the dominoids. This java code creates all the translations boxes given the minoid order. 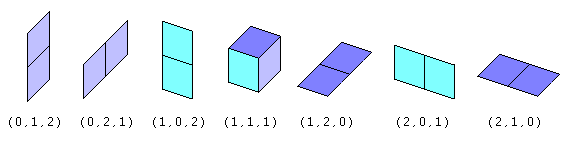 |
|
These are all the rotations' boxes for bounding all the tetrominoids. This java code creates all the rotations boxes given the minoid order. 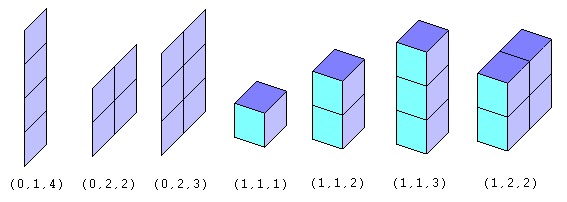 |
Minoids Connections
| The four Soft Connections | The eight Hard Connections | The twelve All Connections |
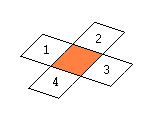 |
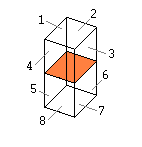 |
 |
The soft and hard connections are shown in the next figures. The coordinates of the minoids and the coordinates of the line connections are included.
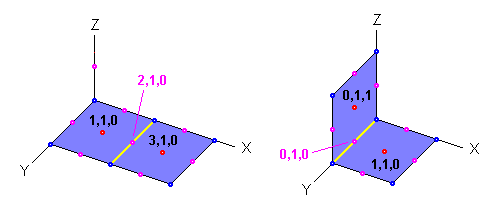
 The soft connections are 'weak' bounds between the minoids, since is difficult to get
physical minoids mantain rigidity with soft connections. In the other hand, the hard
connections are 'strong' bounds between the minoids because is possible to get physical
thick minoids with hard connections.
The soft connections are 'weak' bounds between the minoids, since is difficult to get
physical minoids mantain rigidity with soft connections. In the other hand, the hard
connections are 'strong' bounds between the minoids because is possible to get physical
thick minoids with hard connections.
Three steps at the right describe how to construct a real minoid.
- Figure A shows the ideal minoid inside the unit lattice.
- Figure B shows how the minoid is expanded into an octahedron. This octahedron fills completly the space, and is capable to connect to other octahedra by its faces. This is exactly the hard connection. The octahedron face is an isocelles triangle with 2 units base and the other two sides of length square root of 3.
- Figure C shows the octaedra truncated from the north and south vertices in such a way we get a thick minoid capable to holding hard connections. The final body is a decahedron. The connection is made attaching two minoids by their trapezoidal faces, leaving the square face always free. Then, the eight trapezoids represents the eight possible hard connectors of the minoid.
The two types of connections (soft and hard) give three types of polyominoids:
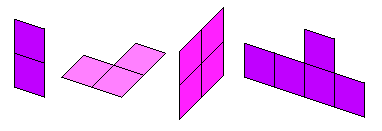
- Soft polyominoids
-
Technically these polyominoids are just polyominoes, e.g. ALL minoids
connections in polyominoes are 'soft', the only permited connection. Examples:
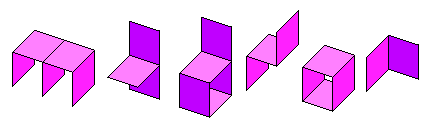
- Hard polyominoids
-
Are those polyominoids (no polyominoes) having ALL minoids connections 'hard'.
This polyominoids can be constructed physically with the decahedron mentioned above.
All the constructions are totally rigid. Examples:
- Mixed polyominoids
-
Are those polyominoids (no polyominoes) having at least one connection 'soft' and
at least one connection 'hard'. Since the soft connection required, the constructions
are not totally rigid, except in few cases we are going to mention.
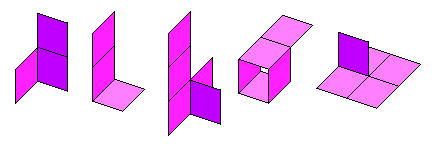
Look the next pentominoid, is rigid. Even though minoids 4 and 5 are soft connected, at the same time, they are hard connected too, through the rest of the minoids 1, 2 and 3. Is hard or mixed connected? The actual software routines say is mixed, then the rigidity must be figured out by other means.:
Translations Polyominoids Counting
- Counts All the polyominoids, that is Total = Mixed + Hard + Soft
- Counts only the hard ones separately.
- Counts the soft ones separately.
Mixed = All - Hard - Soft
The counting is in this way since there are computed bits mask to detect minoids connections, pair by pair. The masks used are of three types: any, hard or soft, and are figured out before the counting takes place.Every 5-minoid inside the Box(1,2,3) is represented as a set of 29 bits, 5 ones and 24 zeros. First an incrementing process takes place to move the 5 bits inside the 29 bits space. This reach the total number of testings to the binomial coefficient of 29 over 5, or
29*28*27*26*25 / 1*2*3*4*5 = 118,755
...instead of working wiht the very big number of 229 of ordinary binary counting.The 118,755 resulting 5-ones numbers are compared against 6 previouly prepared masks to determine if the suspected pentominoid reaches all the walls of the box for fullfill with the boundings. This java code performs the binomial coefficients incremental machine and checks if the polyominoid bits number satisfy the 6 bounding conditions.
Finally the polyominoids fullfilling the bounding are tested for their total connectivity of the 5 minoids, whether any, hard or soft connection were selected in turn. This java code checks if the already bounded polyominoid bits number satisfy a particular connectivity type.
Minoids' interesting Java Code
public boolean isAnyConnected(Minoid other) {
return (isHardConnected(other) || isSoftConnected(other));
}
public boolean isHardConnected(Minoid other) {
dx = Math.abs(x - other.x);
dy = Math.abs(y - other.y);
dz = Math.abs(z - other.z);
if (dx == 0 && dy == 1 && dz == 1)
return true;
if (dx == 1 && dy == 0 && dz == 1)
return true;
if (dx == 1 && dy == 1 && dz == 0)
return true;
return false;
}
public boolean isSoftConnected(Minoid other) {
dx = Math.abs(x - other.x);
dy = Math.abs(y - other.y);
dz = Math.abs(z - other.z);
if ((x & 1) == 0 && dx == 0) {
if ((dy == 2 && dz == 0) || (dy == 0 && dz == 2))
return true;
} else if ((y & 1) == 0 && dy == 0) {
if ((dx == 2 && dz == 0) || (dx == 0 && dz == 2))
return true;
} else if ((z & 1) == 0 && dz == 0) {
if ((dx == 2 && dy == 0) || (dx == 0 && dy == 2))
return true;
}
return false;
}
|
This java code creates all the translations boxes given a minoids order:
public static Box[] getAllTranslationsBoxes(int order) {
int x, y, z, total, count = 0;
Box[] boxes = null;
for (boolean counting = true; true; counting = false) {
for (x=0; x <= order; x++) {
for (y=0; y <= order; y++) {
for (z=0; z <= order; z++) {
total = x*y*(z+1) + x*(y+1)*z + (x+1)*y*z;
if (total >= order && (x+y+z) <= (order + 1)) {
if (counting)
count++;
else
boxes[count++] = new Box(x, y, z);
}
}
}
}
if (counting)
boxes = new Box[count];
else
return boxes;
count = 0;
}
}
|
This java code creates all the rotations boxes given a minoids order:
public static Box[] getAllRotationsBoxes(int order) {
int x, y, z, total, count = 0;
Box[] boxes = null;
for (boolean counting = true; true; counting = false) {
for (x=0; x <= order; x++) {
for (y=x; y <= order; y++) {
for (z=y; z <= order; z++) {
total = x*y*(z+1) + x*(y+1)*z + (x+1)*y*z;
if (total >= order && (x+y+z) <= (order + 1)) {
if (counting)
count++;
else
boxes[count++] = new Box(x, y, z);
}
}
}
}
if (counting)
boxes = new Box[count];
else
return boxes;
count = 0;
}
}
|
This java code checks if the polyominoid bits number satisfy bounding conditions:
private void countTranslations(int order) {
if ((order < 1) || (order < minOrder) || (order > maxOrder))
return;
translations = 0;
if (storeMinoids)
vector = new Vector();
Bits number = new Bits(maxOrder, order);
recursiveCounting(number, maxOrder, order - 1);
}
private boolean allWallsReached;
private void recursiveCounting(Bits number, int bits, int ones) {
// If at least one check fails do not count
allWallsReached = true;
for (int j=0; j < boundingWallsCheckersBits.length; j++)
if (boundingWallsCheckersBits[j].isClearAfterAndWith(number))
allWallsReached = false;
if (allWallsReached && isConnected(number)) {
translations++;
if (storeMinoids)
vector.addElement(number);
}
if (ones < 0)
return;
Bits mask = new Bits(maxOrder, bits);
mask.doNot(); // set up a upper mask;
mask.doOrWith(new Bits(maxOrder, ones)); // set up a lower mask
mask.doAndWith(number); // put the number inside the window
Bits window = new Bits(maxOrder, 0);
window.setBit(ones);
for (int j=1; j < (bits - ones); j++) {
window.shiftLeft(false);
Bits nextNumber = new Bits(mask);
nextNumber.doOrWith(window);
recursiveCounting(nextNumber, ones + j, ones - 1);
}
}
|
This java code checks if the already bounded polyominoid bits number satisfy connectivity:
private Bits visitedBits = new Bits();
private boolean isConnected(Bits number) {
if (number.isClear())
return false;
visitedBits.set(maxOrder, 0);
Bits rotor = new Bits(maxOrder, 1);
int pos = 0;
while (rotor.isClearAfterAndWith(number)) {
rotor.shiftLeft(false);
pos++;
}
// check the seed as visited
visitedBits.doOrWith(rotor);
recursiveConnected(pos, number);
return (visitedBits.equals(number));
}
private void recursiveConnected(int p, final Bits number) {
Bits mask = new Bits(connectionsBits[p]);
Bits rotor = new Bits(maxOrder, 1);
for (int pos=0; pos < maxOrder; pos++, rotor.shiftLeft(false)) {
if (rotor.isNotClearAfterAndWith(mask)) {
if (rotor.isNotClearAfterAndWith(visitedBits)) {
continue; // avoids closed loops
} else if (rotor.isNotClearAfterAndWith(number)) {
visitedBits.doOrWith(rotor);
recursiveConnected(pos, number);
}
}
}
}
|
Jorge Luis Mireles Jasso
October 20, 2001
Torre�n, Coah. M�xico
Also in this site: