Equilateral Pentagons

Equilateral Pentagons E₅ are polygons with five sides of equal length. There are an infinite number of distinct E₅ since the internal angles can take practically any real value. Next java applet shows some familiar geometric shapes disected into E₅s. Where the disection is not unique, an animation shows some possibilities. A selector permits to switch between all the figures.

Java source code:
StickPoint.java and SticksApplet.java

Theory

Only four intersected equal circles are enough to define a E₅. The center of each circle corresponds to one vertex of E₅ namely angles e, a, b and c. The fifth vertex d is determined by the intersection of circles C1 and C4 which gives the smaller angle.

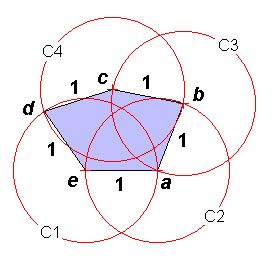
Only two angles are enough to determine the positions of the four circles, so E₅ can be defined as a two-variable-function:

E₅ = F(a, b)

Conditions for Simplification

In order to avoid reflections, translations, rotations (and complications) of a given E₅ two conditions can be stated:

d must be the smaller of the five angles.

(d <= a) && (d <= b) && (d <= c) && (d <= e)
a must be greater or equal than b.

a >= b

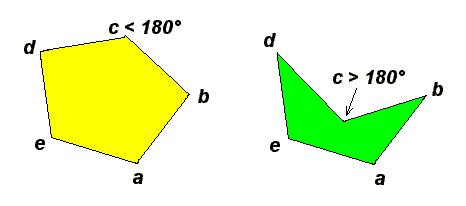
In the following figures we can see how only one E₅ is valid among six variations. Figure 1 (in cyan) satisfies both conditions. Figures 2-5 (in green) doesn't satisfy first condition while Figure 6 (in yellow) satisfies first conditions but don't satisfy the second one.

Covex and Concave E₅

The angle c's values determine the convexity of E₅. We can conclude that:

E₅ is CONVEX if angle c is lower than 180^o.
E₅ is CONCAVE if angle c is greater than 180^o.

Self-Intersecting for E₅

The angles a and b values determine the self-intersecting of E₅. We can conclude that:

E₅ is not self-intersected if:
2a + b is greater than 180^o.
E₅ is self-intersected if:
2a + b is lower than 180^o.

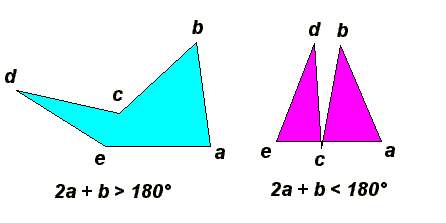
Some Trigonometry of E₅

To find the values of angles c, d and e as functions of (a, b) some calculations and the following figure can help:

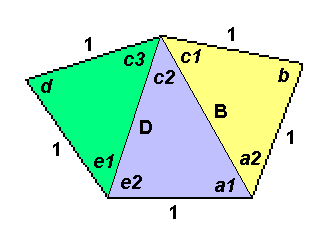
Here E₅ is divided into three triangles. Two triangles (left and right) are isoceles. The triangle at the center is more general. Some angles have being divided too in this way:

a = a1 + a2
c = c1 + c2 + c4
e = e1 + e2

By trigonometry from yellow triange we found that:

a2 = c1 = p/2 - b/2
a1 = a - p/2 + b/2
B = 2 * sin(b/2)

From purple triangle we found that:

D² = 1 + B² - (2)(1)(B) * cos(a + b/2 - p/2)

D² = 1 + 4*sin²(b/2) - 4*sin(b/2)*sin(a + b/2)

Now, having D, the angle d value can be calculated from green triangle:

d = cos^-1 [ cos(a) + cos(b) - cos(a + b) - 1/2 ]

With more calculations (too complicated to be included here) we found angle e is:

e = tan^-1 [

sin(a + b) - sin(a)

-------------------------

cos(a) - cos(a + b) - 1

] + 1/2 * (p - d)

Finally angle c value is (yours better equation is welcome) is:

c = (5/2)*p - a - b - d - e

Minimums and Maximums of the angles

Having three angles c, d and e as functions of other two (a,b), I have drawn a lot of beatiful families of curves, they are still drawn on real paper. I hope soon have time to include them here as electronic media... Also, other information such as area, angles' relations can be plotted too... Analysing angles plots we get some results: For No-self-intersected E₅ these are the ranges for the angles:

Minumum Maximum
a 60^o 120^o

b 28.9^o 108^o

c 108^o 331^o

d 0^o 108^o

e 75.5^o 240^o

Equilateral Polygons' To-Do

There is a lot of material (original to be included, and not original to be mentioned) next to be added as time permits...

An applet for drawing the plots of functions F(a, b).
From the 14 know convex pentagons tesselations of the plane, some has equilateral pentagons...
There are also some tesselations with more than one type of and/or concaves equilateral pentagons.
Polyominoes are in fact equilateral polygons (The pentominoes are equilateral dodecagons E₁₂). These dodecagons have only few internal angles values: 0^o, 90^o, 180^o, 270^o and 360^o. These discrete angles surely simplifyes in some way the families of equilateral polygons.
A Math verse reads ...every conic curve can be determined by 5 points... Therefore exits a conic curve touching the 5 vertices of every E₅. I'm writing a Java applet for drawing conics touching all the general E₅ vertices. The relations between conic's and E₅'s parameters should be interesting.
I made some calculations for equilateral hexagons (though complicated). Three angles are needed for the hexagons. While E₅ needs surface plots, E₆ needs three-dimensional plots. Altough, more conditions can be imposed to the angles to get a reduced set. For instance, families of symmetric equilateral hexagons having their angles values of the form 2p / n, being n an integer, tile the plane chaotically.
Determine minimum solutions for dissections of E_Ms into E_Ns. wheter M > N, M = N, M < N. There are systematic solutions by software?

Chaotic Tiling with Equilateral Polygons

The rhombi are equilateral tetragons or E₄. Only one angle is needed for their description. Exists one pair of rhombi for chaotic tesselation. Also exist one triplet of rhombi for chaotic tesselation, and one quartet, one quintet and so on...
Penrose tiling figure taken from an internet site
The CHAOS TYLES are two equilateral pentagons Their angles are (80^o, 160^o, 60^o, 140^o, 100^o) and (40^o, 200^o, 60^o, 100^o, 140^o). Applying the notation mentioned above we have this tiles are E₅(100^o, 80^o) and E₅(100^o, 60^o).
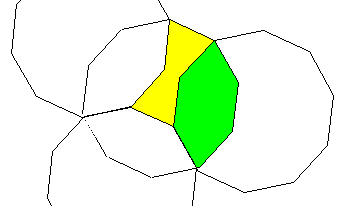
Two symmetric equilateral hexagons I found in 1997 by drawing regular decagons, seems can tile chaotically the plane. Their shapes recall us the main two types of optics lenses:
- Convex with angles (72^o, 144^o, 144^o, 72^o, 144^o, and 144^o)
- Concave with angles (72^o, 72^o, 216^o, 72^o, 72^o, and 216^o)
can we name them lenses?.
Open questions:
- There exists three E₅ for doing chaotic tiling, four? more?
- There exists 2, 3, 4, ... E_n (yes, n) for doing chaotic tiling?

Jorge Luis Mireles Jasso
Torre�n, Coah. M�xico.
April 4, 2002

Also in this site:

The Polyominoids

Hosted by www.Geocities.ws