Para navegar pela página use as barras de links superior e vertical
Por que existem apenas cinco Poliedros Regulares de Platão?
É fácil entender por que há somente cinco poliedros
regulares se, usando sólidos construídos com cartolina, fizermos sua planificação.
nivelando os cantos de um poliedro, a soma dos ângulos dos polígonos unidos em cada
vértice será menor que ![]() . Considere as
possibilidades de união de polígonos regulares. é claro , necessitamos, no mínimo,
três faces unidas em cada vértice para formar um sólido.
. Considere as
possibilidades de união de polígonos regulares. é claro , necessitamos, no mínimo,
três faces unidas em cada vértice para formar um sólido.
Triângulos -
Cada ângulo de um triângulo equilátero mede ![]() .
Teremos as seguintes possibilidades:
.
Teremos as seguintes possibilidades:
Número de triângulos equiláteros |
Soma dos ângulos |
Poliedros formados |
3 |
|
Tetraedro |
4 |
|
Octaedro |
5 |
|
Icosaedro |
6 |
|
Impossível |
![[Maple Bitmap]](p_platao01.gif)
Quadrados - Um quadrado tem 4 ângulos de ![]() , então podemos fazer a seguinte
união em cada vértice.
, então podemos fazer a seguinte
união em cada vértice.
Número de quadrados |
Soma dos ângulos |
Poliedros formados |
3 |
|
Cubo |
4 |
|
Impossível |

Pentágonos - Cada ângulo de um pentágono
mede ![]() . Deste modo unindo três
pentágonos obtemos
. Deste modo unindo três
pentágonos obtemos ![]() em cada
vértice e o poliedro formado é um dodecaedro:
em cada
vértice e o poliedro formado é um dodecaedro:
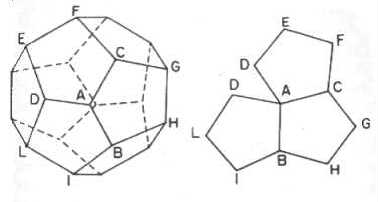
Hexágonos ou mais lados - Cada ângulo do hexágono mede ![]() . Juntando três hexágonos , a soma
dos ângulos seria
. Juntando três hexágonos , a soma
dos ângulos seria ![]() , então não
é possível nenhum poliedro com faces hexagonais. Similarmente não é possível nenhum
poliedro com faces de 7 lados ou mais.
, então não
é possível nenhum poliedro com faces hexagonais. Similarmente não é possível nenhum
poliedro com faces de 7 lados ou mais.
Assim, há somente cinco poliedros regulares. São os seguintes:
| Poliedro | Número de Faces |
Tipo de Face |
| Tetraedro | 4 |
Triângulo |
| Hexaedro ( Cubo ) | 6 |
Quadrado |
| Octaedro | 8 |
Triângulo |
| Dodecaedro | 12 |
Pentágono |
| Icosaedro | 20 |
Triângulo |

