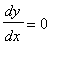Para navegar pela página use as barras de links superior e vertical
O dia-a-dia esta cheio de tais problemas e é natural que os matemáticos e outras pessoas os considerem interessantes e importantes. Um homem de negócios procura maximizar lucros e minimizar custos. Um engenheiro ao projetar um novo automóvel deseja maximizar a eficiência. Um piloto de linha aérea tenta minimizar o tempo de vôo e o consumo de combustível.
Em ciências, nós muitas vezes, achamos que a natureza age de maneira a maximizar ou minimizar uma certa quantidade.
Por exemplo, um raio de luz atravessa o sistema de lentes ao longo de uma trajetória que minimiza o tempo total do percurso, um fio flexível suspenso assume uma forma que minimiza a energia potencial em virtude da gravidade.
Sempre que usarmos termos como esses, podemos dizer que é alguma espécie de problema de máximos e mínimos, e se esse problema puder ser expresso em termos de variáveis e funções, os métodos de cálculo estarão disponíveis para nos ajudar a compreende-lo e resolve-lo.
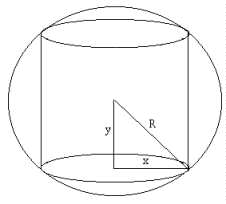
Exemplo - Determine a razão entre a altura e o diâmetro da base do cilindro de máximo volume que pode ser inscrito numa circunferência de raio R
Esboçando o desenho de um cilindro inscrito na esfera e colocando os dados vemos que:
|
|
onde |
 ( ii) ( ii)
|
 |
 |
Visualizando os casos extremos vemos que V
é pequeno quando xesta perto do zero e também quando x esta
perto de R, e assim entre esses extremos existe uma posição de volume
máximo. Para acha-la, substituímos o valor de ![]() de (ii ) em (i )
de (ii ) em (i )
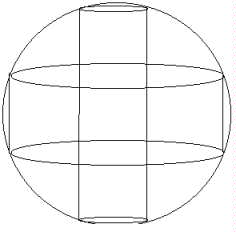
Igualando a zero para achar y e daí usando ( ii ) para achar x temos:
A razão da altura e o diâmetro da base maior do cilindro é, portanto,
Esse resultado pode ser obtido de modo mais eficiente pelo método de derivação implicita.
|
|
|
ou | 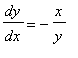
|
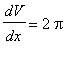 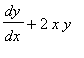
|
|
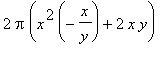 |
= |

|
portanto, segue-se
que 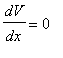 quando
quando  ou
ou 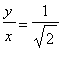 =
= ![]()


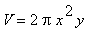 (
i )
(
i )![[Maple Math]](max_min06.gif)
![[Maple Math]](max_min07.gif)
![[Maple Math]](max_min08.gif)
![[Maple Math]](max_min09.gif)
![[Maple Math]](max_min10.gif) e
e ![[Maple Math]](max_min11.gif) =
= ![[Maple Math]](max_min12.gif)
![[Maple Math]](max_min13.gif) =
= ![[Maple Math]](max_min14.gif)