Para navegar pela página use as barras de links superior e vertical
O método de Exaustão de Eudoxo é rigoroso mas estéril. Em outras palavras, uma vez conhecida uma fórmula, o método de Exaustão pode se Constituir num elegante instrumento para prová-la, mas o método por si só, não se presta para a descoberta inicial do resultado. Quanto a esse aspecto, o método de exaustão assemelha-se muito ao principio de indução finita. Como então Arquimedes descobriria fórmulas que tão elegantemente demonstrava pelo método de exaustão?
Somente com a descoberta do livro O Método em 1906 foi-se possível responder a esta pergunta.
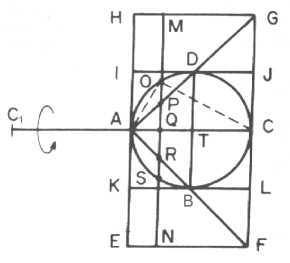
Sejam ABCD um círculo com diâmetros perpendiculares AC e BD
; AFG um triângulo ( retângulo em A ) isósceles, com base FG
e altura AC ; e EFGH um retângulo. Girando esta figura em torno
do eixo ![]() obtemos: uma esfera,
gerada pelo circulo ABCD ; um cone, gerado pelo triângulo AFG ;
e um cilindro, gerado pelo retângulo EFGH .
obtemos: uma esfera,
gerada pelo circulo ABCD ; um cone, gerado pelo triângulo AFG ;
e um cilindro, gerado pelo retângulo EFGH .
Seja MN uma reta do plano como na figura acima, perpendicular a AC , cortando este segmento no ponto Q.
Como QP = AQ e o triângulo OAQ é retângulo, temos:
|
Como |
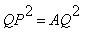 |
e |
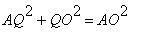 |
|
temos que |
|
Por outro lado, o triângulo OAC é retângulo em O e OQ é perpendicular a AC , logo, por semelhança de triângulos entre os triângulos AOC e AOQ temos que,
|
|
= | |
|
e usando a primeira igualdade, |
|
, então, |
|
|
, |
donde obtemos, notando que QM = AC e tomando ![]() =
AC,
=
AC,
|
|
||
|
|
= |
Portanto,
|
|
ou |
|
|
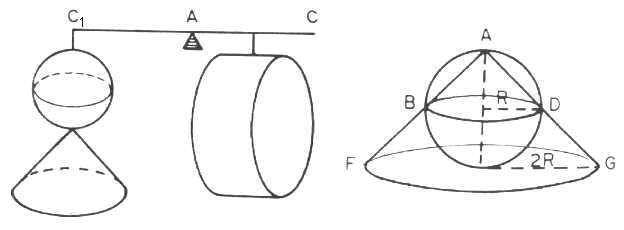
Esta relação é agora interpretada como traduzindo o equilíbrio dos
pesos numa alavanca ![]() com apoio em
A . De fato, pela lei da alavanca ( dada pelo próprio Arquimedes em
seu livro " Sobre o equilíbrio de figuras Planas " ), e relação
acima nos diz que os círculos de raios QP e QO , quando
transferidos para
com apoio em
A . De fato, pela lei da alavanca ( dada pelo próprio Arquimedes em
seu livro " Sobre o equilíbrio de figuras Planas " ), e relação
acima nos diz que os círculos de raios QP e QO , quando
transferidos para ![]() , equilibram o
círculo de raio QM localizado em Q . (Nesse raciocínio estamos
imaginando os pesos dos círculos proporcionais às suas áreas.) Até aqui o
raciocínio matemático é perfeitamente rigoroso, mas agora vem a parte heurística
do argumento; consideramos o cilindro como união infinita dos círculos de
raio QM , Q variando de A até C ; e analogamente
para a esfera e o cone. Remontamos a esfera e o cone no extremo
, equilibram o
círculo de raio QM localizado em Q . (Nesse raciocínio estamos
imaginando os pesos dos círculos proporcionais às suas áreas.) Até aqui o
raciocínio matemático é perfeitamente rigoroso, mas agora vem a parte heurística
do argumento; consideramos o cilindro como união infinita dos círculos de
raio QM , Q variando de A até C ; e analogamente
para a esfera e o cone. Remontamos a esfera e o cone no extremo ![]() da
alavanca ( como na figura abaixo ) e concluímos que esses sólidos devem
equilibrar o cilindro com centróide no extremo T da alavanca, onde
da
alavanca ( como na figura abaixo ) e concluímos que esses sólidos devem
equilibrar o cilindro com centróide no extremo T da alavanca, onde 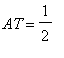 AC
. ( Agora o peso dos sólidos são tomados como proporcionais a seus volumes.
) Então, sendo
AC
. ( Agora o peso dos sólidos são tomados como proporcionais a seus volumes.
) Então, sendo ![]() ,
, ![]() e
e
![]() os volumes da esfera, do cone e
do cilindro respectivamente, teremos:
os volumes da esfera, do cone e
do cilindro respectivamente, teremos:
![[Maple Math]](esfera_cilind25.gif) =
=
![]() ,
,
|
ou seja, |
Arquimedes já sabia que ![]() .
Substituindo este resultado na equação anterior e simplificando, vem:
.
Substituindo este resultado na equação anterior e simplificando, vem:
![]() , mas como
CG = 2 TD , segue-se que o volume do cone é 8 vezes o volume do
cone obtido por rotação do triângulo ABD , como ilustra a figura
acima, isto é:
, mas como
CG = 2 TD , segue-se que o volume do cone é 8 vezes o volume do
cone obtido por rotação do triângulo ABD , como ilustra a figura
acima, isto é:
![[Maple Math]](esfera_cilind32.gif) , onde R
é o raio da esfera. Daqui e de
, onde R
é o raio da esfera. Daqui e de ![]() ,
resulta finalmente a formula do volume da esfera.
,
resulta finalmente a formula do volume da esfera.
![[Maple Math]](esfera_cilind34.gif) .
.


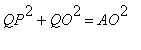


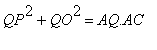

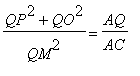
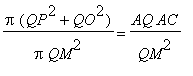
 .
.