Rubik's XV

An expanded version of Jaap Scherpuis' Solution

Solve the Back Side

For the back side, you have to come up with a magic sqaure, where each row, column and diagonal add up to the same sum. In the example abouve, they each add up to 15, but you can use any other sum ranging from 12 to 36.

The 9 tiles that appear on the back are the same tiles that lie in the 9 central squares on the front. The yellow tiles (1 thru 15) have the same numbers as the red tiles (I thru XV) with the asterisk as zero.

Magic Square, front side solved	Magic Square, back side solved
Note how the front and back sides are mirror images of each other

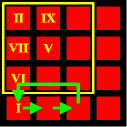
You must solve the puzzle from the front side, concentrating on those 9 central squares. But instead of solving the 1st column as I, V, IX and XIII, solve the 1st column as II, VII, VI, and any other tile. The same goes for the next two columns; solve the 2nd column as IX-V-I-any (instead of II-VI-X-XIV), and solve the 3rd column as IV-III-VII-any (instead of III-VII-XI-XV). Ignore the 4th column altogether.

Hint: Do not use place a tile on the bottom row that you may need for the magic square itself. If you do, then you'll have to dig it out later on.

So, use the exact same moves you used while solving the front side. In case you have to dig out a tile from the bottom row (without disturbing the Magic Square itself), use these new moves:

B MR C MR B MR C MR B LMR C LMR B LMR C LMR	B R C R B R C R B MR C MR B MR C MR

@ Introduction/Notation @ Solve Columns 1 and 2
@ Solve Columns 3 and 4 @ Solve the Back Side

Return to Mathematica

Hosted by www.Geocities.ws