 | Vol. 1 No. 1 2001 |
LOGIC, THE PHILOSOPHY OF SYSTEMATIC THINKING
AND ARGUMENTATION
F.P.A. Demeterio III
There was a time in the history of education, where being educated meant having gone through just a handful of subjects, among which are music, mathematics, rhetoric and philosophy, with philosophy occupying a certain pre-imminence. That time was medieval Europe, a far-away place in the far-away past. Many changes had occurred since. Throughout the centuries culture and knowledge had evolved into what we call today the modern times. At present being educated means having gone through the ever growing literature of an ever narrowing discipline, and philosophy is no longer considered pre-imminent -- in fact, far from being pre-imminent. Many students seem to be bewildered about the nature of this subject. While some are expecting to glean exotic knowledge, others are simply disgusted at the thought of its endless debates and hundreds of hairsplitting distinctions.
To large extent the students' attitude towards philosophy is due to its notion's wrong understanding to begin with. Professors of philosophy are partly to be blamed. They usually start a philosophy course with a supercilious citation of its etymology filos (philos) and sofia (sophia), love for wisdom, with wisdom invariably taken as the venerable wisdom of ages past. This meant that if students were to love wisdom, they have to plow through the hoary maxims and aphorisms left by a horde of famous dead men! Certainly, philosophy seen this way could mean something exotic on one hand or plainly disgusting on the other.
With a little linguistic excursion into the classical and Homeric Greek, the roots filos and sofia need not be interpreted as love for wisdom. They could more basically mean love to exercise one's curiosity. With this more originary meaning, we realize that there nothing exotic nor disgusting with philosophy. It is not about rummaging through musty manuscripts of great dead men. Rather it is about our living desire to understand the world that surrounds us and the world that is within us. If man is indeed a knowing being, then philosophy is in fact closer to our real nature than we previously thought. It is through the exercise of our curiosity that we become a real knowing being.
Taking a course in philosophy, is a little bit different from taking other courses from the languages, or mathematics or the natural and social sciences. Here, we don't start with the thick list of things the students should learn after taking the course. Rather, we merely aim at a few things. First, that the students may rediscover the joy of being consumed by a childlike curiosity; and second, that they may learn to ask the right questions and know the preliminaries how to find answers, no matter how provisional these answers would turn out to be.
Logic started as a tool for philosophy, a way of looking for provisional answers to life's questions. But lately, other disciplines have appropriated it both to their advantage and to logic's further development. Today, logic is no longer an exclusive private property of philosophy, but mathematics, linguistics and computer science also claim rightful co-ownership of it.
The name logic is derived from Greek root logos (logos), a word which can mean a number of things, from word to measure, to reason and can even take personified meaning of a demi-god, and many others beside. But it is reason which is the particular meaning of logos rom which logic is derived. Hence, etymologically, logic means the study of human reasoning, or thinking. Logic helps man in discriminating the cogent reasoning or thinking from the uncogent. During the ancient and medieval periods, in Europe, when philosophy, theology and law were practically the only legitimate areas of knowledge, logic had been very prestigious. It had been the sole and the most effective tool for philosophers and theologians to use for their metaphysical speculations, and an excellent training ground for lawyers to hone their rhetorical skills. However, with the multiplication of the areas of knowledge occasioned by the scientific revolution, the old trio of philosophy, theology and law lost their monopolistic claim to legitimacy. Philosophy and theology each formerly claiming to be queen of the sciences, declined and found refuge only in the nooks and crannies of the universities. Law maintained its old glory but left behind its dependence on rhetoric. With these dramatic changes, logic lost its ancient and medieval popularity.
We might as well pause at this point and ask: "If the ancient and medieval concerns for logic are gone, then why do we -- students of the 21st century -- have to study this dead artifact of the past ages?" "Does not logic properly belong to the museums of medieval history?"
Though the socio-cultural upheavals have swept aside philosophy, theology and the lawyer's rhetoric, that does not mean that logic has also to be swept aside. Logic is a tool for knowledge and man's quest for knowledge is very much still with us, and in fact the contemporary times had only intensified this quest. The need for systematic thinking and argumentation, then, should not wane with the waxing of man's quest for knowledge.
A rather pessimistic saying goes: "Life is just one problem after another." Critical thinking taught us never to accept old clich�s at face value, but there is simply much truth in this particular saying. Life is certainly one big series of problems. That means to approach life squarely is to solve its series of problems. To solve life's problems one needs to think, to reason out and to argue -- either against others or against oneself just as what happens when one weighs the pros and cons before making an important decision. We are not implying, however, that only those who have studied logic can steer through the problems in life successfully. We can solve many of life's problems even without knowing the word logic in the first place, but with the help of logical training we can approach these problems more systematically and more efficiently. In fact, logic has a very practical and fundamental value to human life.
Taking man as just one of the various species in the animal world, he could easily qualify as the weakest of them all and the most poorly equipped species for survival. If man triumphantly emerged through the fierce competition for survival, it is because unlike other animals, he can think and store knowledge. Knowledge is not only important for human survival, it has lately become necessary to cope up with the sophistication of culture and society. Man has become more and more a creature of knowledge, as the modern world has transformed into a regime of knowledge.
There are two basic types of knowledge: first, knowledge of facts, or the simple and unstructured knowledge that is directly acquired from the real world; and second, complex, or structured knowledge, that is built from simple knowledge by the use of much thinking and speculation. Whereas knowledge of facts does not require much mental effort, for it is directly acquired from the real world, complex knowledge does. That the sky is blue, or the field is green are examples of knowledge of facts. Chemistry, physics, the humanities are examples of complex knowledge, and so are the hunting techniques of the Cro-Magnon, or the agricultural methods of a first farmers, or the highly advanced organizational skill of a corporate executive. The modern world demands from man more and more complex knowledge. In order to survive in such a world man has to deal with an ever growing bodies of complex knowledge.
To create or to work with complex knowledge, man needs systematic thinking. Again, we are not implying here that only those who have studied logic can effectively cope with the modern world's flood of complex knowledge. Man has a natural knack for systematic thinking, but this knack can be greatly enhanced and developed through the study of logic. In fact, even Aristotle had already suggested that logic is an excellent preparation for the study of any discipline.
The continuous rise of science and technology have brought an unprecedented growth in the field of mass communication. An event in a far flung corners of the country can almost be instantaneously circulated nationwide through radio and telecommunication. Issues from the hot plains of Africa, or from the icy regions of the Poles can likewise be known almost immediately via satellite. Moreover, in the last decades we have witnessed the commercial launching of the inter-net, dubbed by many as the highway of information.
Man is now being bombarded with a staggering dosage of information. No doubt, this bombardment has aided a lot in educating him. Yet it also helped a lot in mis-educating him. The technological devices for mass communication are indeed the media for truth, but they are also the same media for lies. And the worst thing is these technological devices would not tell us which among heap of information is valuable and which is rubbish. One local expert in the inter-net had commented that only 10% of the information in the inter-net can be properly called reliable information. The study of logic can help us in dealing with the modern world's over exposure to information in two ways. First, logic teaches us to be critical, it gives as the questioning attitude and the impulse to ascertain things first before accepting them. Second and more specifically, logic teaches us the different patterns of lies, the liar's modus operandi so to say. By knowing the patterns of lying in advance, we are forewarned and hopefully will not end up their miserable victims. Since the time of Aristotle, the study of lies or fallacies has been considered an integral part of logic.
If you have not said these words yet, I bet you will say these sooner or later. "How can I do without my computer?" If modernization had given machines and equipment to the working class to make them more efficient, it has given the computer to the thinking and the clerical class to help them cope with the knowledge regime. Modern life needs computers for their precision and efficiency.
Life would really be complicated without the computers. If you agree with that statement, then you should agree that life would really be complicated without logic, because in programming these remarkable machines symbolic logic, a modern logical system, is needed. There is no sense then in saying, why should man be logical when computers can do logic for him.
Hence, for reasons of practicality, for coping up with the knowledge regime, for being wary about truth and lies and for the further development of the cyber technology logic should remain important. Though the ancient and medieval popularity of logic has waned considerably, practically all universities in the world maintained their faith on it. Logic remained to be acknowledged as having a significant role to play in general education, and in preparations for the study of the different modern disciplines. In many universities today, logic is gradually taking the place of the study of classical languages as training for canonical thinking and writing.
An argument is a system of claims, or statements, one of which is meant to be supported by the others. The definition basically means two things. First, an argument, has to be an aggregate of claims. Second, it is not just any aggregate of claims; rather, it is an aggregate that is governed by a particular system: the system that specifies that one of the claims be intended to be supported by the other claims. Hence the following aggregate
is not an argument for the reason that none of its claims is meant to be supported by the other claims. While the following aggregate
is an argument for the reason that its third claim is supported by its first and second claims. The length of an argument is measured by its number of claims. An argument can be short as
or it can run through thousands and thousands of claims. Dissertations and some books are known to prove only one claim, and in themselves they are lengthy arguments.
As a system of claims, the argument has its basic structure. For this matter, all argument are composed of two parts and a single process. In the above mentioned arguments the claims Justice demands that the government should do something on our system and So she is attractive are the conclusions.
In the above mentioned arguments the claims Every Filipino is entitled to have the minimum means to meet his basic needs, Yet, presently, thousands, if not millions of Filipinos could not meet their basic needs and The girl is very beautiful are the premises.
The inference is the mental act of deducing new information from a pre-given information. We cannot exactly explain how the mind does it, but we know and even can feel our mind doing it. At this point we are going to deal more closely with this somewhat mysterious process by highlighting its role in problem solving.
For instance, we have this problem:
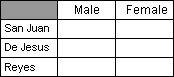
Here, we have two premises to start with "San Juan is the half-brother of De Jesus" and "De Jesus has a grandson named Reyes." Through the process of inference, we are required to produce a conclusion that would settle who among the three persons is the female. Since we are required to do a number of inferences here, it will be advantageous for us to tabulate the result of each inference.
Since San Juan is a half-brother, he must be male. Since Reyes is a grandson, he too must be male. Looking at our table, we have made the following inferences.
Since the problem presupposes that at least there is one female among the three, through the process of elimination we ascertain that De Jesus must be the female.
We arrived at the conclusion that De Jesus is female through a series of inferences based on the two given premises.
Let us take a look at another problem.
Here we have five premises to work with to come up with the required conclusion that would identify each individual's profession. Again, we have to tabulate our inferences.
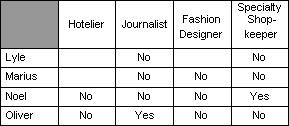
Since Lyle and Oliver are regular customers of the specialty shop, surely none of them is the shopkeeper. Since the fashion designer created Marius and Noel's wardrobe, and would not wear his own designs, definitely none of them is the fashion designer. Since Noel has never been to the hotel, he is not the hotelier. Since the journalist previously featured Marius and Noel and is planning to interview Lyle, then none among the three is the journalist. So far, we have the following inferences gleaned directly from the given premises.
Again, by elimination we can complete the table. Since Noel is not the hotelier, nor the journalist, nor the fashion designer, then he must be the specialty shopkeeper. Since the journalist is not Lyle, nor Marius, nor Noel, he must be Oliver. Through elimination we have the added to the table the following inferences.
Again, we can make further elimination. Since, we have identified Noel as the shopkeeper, then Marius is not the shopkeeper. Since, Oliver is the journalist, then he is not the hotelier, nor the fashion designer. From these elimination, we have the additional inferences.
Again from this table, we can make even further elimination. Since, Marius is not the journalist, nor the fashion designer, and nor the shopkeeper, he must be the hotelier. Since the fashion designer is not Marius, nor Noel, nor Oliver, he must be Lyle. And if Lyle is the fashion designer, then he is not the hotelier.
Now, the table is complete. Lyle is the fashion designer, Marius is the hotelier, Noel is the shopkeeper, and Oliver is the journalist.
Try to work out the solutions for the following problems.
Reyes, Cruz, San Pedro and De Vera are senior students of San Beda College taking up information science, law, philosophy and accountancy, though not necessarily in that order. Reyes and Cruz are grandsons of the senior accounting professor. De Vera is married to a junior economics student from a nearby exclusive girls' school. The philosophy student has no relatives in San Beda College. The accountancy student is still single. The only accounting professor that Cruz knows is his grandfather. Only the law student is female. What is the course taken up by each student? If we cannot give an exact description how inference is made possible, I guess we can feel its reality as we force ourselves to extract more information from the given premises to come up with the required conclusion. That is inference, without it there is no argument, and there is no logic, and there will hardly be human thinking to begin with.
With the three basic parts of an argument, we can now formulate a more technical definition:
As mentioned earlier, not all aggregates of claims are arguments. Some aggregates can be poetry, or just plain statements about facts or opinions. What makes an aggregate of claims an argument is the particular structure or system that governs the organization of these claims. But sometimes it is admittedly difficult to identify arguments.
Consider this particular aggregate:
Is this aggregate an argument or not? In reality there is no definite answer for such a question. The above mentioned aggregate can be understood in at least three different senses.
In order to avoid such a confusion, arguments are usually equipped with inference indicators. Inference indicators are either premise or conclusion indicators.
By the use of these indicators, the ambiguous aggregate of claims mentioned above can be greatly improved.
or the other way around,
When you make your arguments, or write argumentative essays, try using some of these indicators and you will see great improvements in your style. However, these indicators are not fool proof signs of an argument. There can be claims which carry them though they are not part of any argument. Moreover, in ordinary, or everyday language, these indicators may not appear. In the end, identifying arguments would amount to identifying them by knowing their particular contexts.
There are instances, in day to day situations and even in formal occasions, when parts of arguments are simply not given with the presumption that these unstated parts are already known by both the arguer and his audience.
The unstated premise or conclusion can be considered an authentic part of the argument if it is reasonably clear that the arguer meant it to be understood in the particular manner he intended it to be. For instance, when the advertisers of local fast-food restaurant posts the notice The fries are largest at Burgershop, they presumed that prospective customers can easily get the unstated parts of their argument. Reconstructing their incomplete argument, it would appear somewhat like this
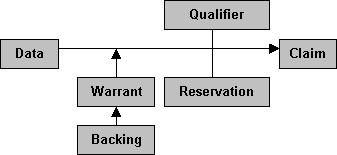
In 1969, the philosopher of science and logician Stephen Toulmin, presented a deeper analysis of the structure of arguments in his work The Uses of Arguments. Instead of just dissecting the arguments into three parts like what we did, Toulmin pointed out that arguments are structurally constituted of six parts, namely data, claim, warrant, backing, qualifier and reservation, which he graphically represented as
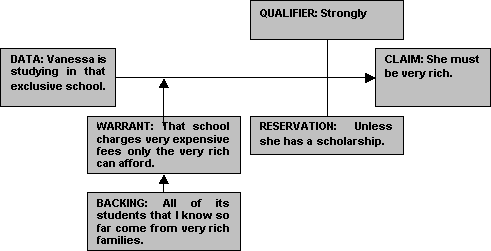
Toulimin's data roughly corresponds with our premise, and may consists of facts, conditions that are immediately observable, beliefs that are taken for granted by both the arguer and his audience, or previously established conclusions. Claim roughly corresponds to our conclusion, it is the thought, opinion or statement which the arguer wants to put forward and be accepted by his audience. Warrant can be expressed in the form of logical and quasi-logical rules, or principles and conventions specific to the contextual field where the arguer and his audience are situated. Backing consists of further data or warrant employed to support and legitimize the content of the warrant. Qualifier is an adverb or adverbial phrase that denotes the rational force of the warrant. Reservation denotes the exceptions to the rule expressed in the warrant. An example of an argument laid out in Toulmin's model is the following.
As we all can sense it, seldom do we find arguments as elaborate as this one. If we streamline this into just to its constituent data and claim, we can have an argument that is just as good. Toulmin noticed this, of course, and in fact he agrees that more often than not arguments either leave the warrant, backing, qualifier and reservation simply implied or they include them in a very hazy manner in either in the data or in the claim. Hence, he stressed that it is in the duty of the one who evaluates and criticizes incomplete arguments, to fill in the missing parts and lay them out in accordance to his model. For that matter, Toulmin's model is in fact not a model of day to day arguments but an ideal pattern for argumentative clarity and precision. This is the reason why logic more usually employs only the simpler dissection of arguments into premise, inference and conclusion, and reserve the Toulmin model for other special cases.
Toulmin's most important point here aside from his idealized argumentative clarity and precision is the demonstration that most of our arguments have in fact a number of unstated parts. That is just very reasonable. When we argue with persons who share most of the background information and belief system that we have, there is hardly any sense in making everything stated clearly in black and white.
As technically defined, an argument should have one conclusion drawn out from the premise or premises through the single process of inference. Yet there are arguments that seem to have a number of conclusions from a number of inferences. And there are arguments that seem to have one conclusion but drawn out through a number of inferences. And there are arguments that appear to have smaller arguments as their parts. The argument Rene is absent again. It looks that he has personal problems. He will surely miss the lessons is an example of a seemingly anomalous argument.
There is really nothing wrong with this type of argument. This is just an incident of two arguments linked together by the fact that they are sharing the same premise Rene is absent today. If the technical definition of an argument specifies that there be one conclusion and one inference, this technical definition pertains only to the simple argument. There is such a distinction between simple and compound arguments. A simple argument is an argument based on a single inference. While a compound argument is an argument based on more than one inference.
Consider the argument:
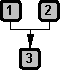
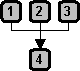
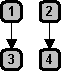
If we follow the flow of the argument it would seem to be okay, yet the conclusion simply feels a little funny and makes us sense that there must be something wrong with this argument somewhere. We can assess the worth of an argument by looking at its structure. Unfortunately, in our day to day life more often we deal with compound arguments and very seldom with simple arguments. It is quite easy to notice the structure of simple arguments. But once an argument runs through several claims and inferences, its structure may no longer appear obvious. Fortunately, Professor Monroe Beardsley, in his book, Practical Logic, published in 1950, proposed a way of charting out the patterns of simple and complex arguments. Beardsley used circles to represent claims and arrows to represent inferences. The Beardsley chart moves from top to bottom. Now, in establishing the structure of the abovementioned arguments, we can start by numbering its claims.
Representing this argument with Beardsley's circles and arrows, we can see that its structure is that of a chain linear argument.
By examining its chain-like structure link by link, we can determine that from claim number 1 to claim number 2, the argument is perfectly okay. But from claim number 2 to claim number 3, here we have the anomaly. Claim number 3 does not flow from claim number 2. There is no guarantee that the more a person knows, the more he forgets things he knew before. From claims number 3 to 4 to 5 and down to 6, the flow is again perfectly okay. The reason why the argument appears okay but a little funny towards the end is it is indeed okay aside from that questionable link between claims number 2 and 3.
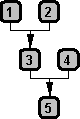
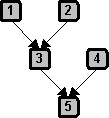
Using the Beardsley chart we can also examine the basic structures of simple and compound arguments.
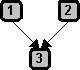
As mentioned earlier, what characterizes the simple argument is its involvement of just a single inference. There can be an indefinite number of patters for simple arguments depending on the number of their premises. The ones that we are going to cover are the most basic patterns.
or
Simple arguments with multiple premise can, theoretically, have an infinite number of premises. So an argument whose conclusion is drawn through a single inference from a hundred or a thousand premises could still be a simple argument.
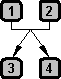
If the involvement of just a single inference is what characterizes the simple argument, then it follows that the involvement of more than one inference is what will characterize the compound argument. There are infinitely much more patterns of compound arguments than there are patterns of simple arguments. What we are going to show here are the most basic patterns.
There are two basic types of arguments, the inductive and deductive. Traditional logic defines each in accordance to their general movements. That means, inductive argument is an argument having premises that talk about particular instances, and a conclusion that talks about generalizations; and deductive argument is the reverse of that, argument having premises that talk about generalizations and a conclusion that talk about particular instances. For reasons that we are going to see later, such definitions though very helpful are lately found to be inadequate. Hence, we have the more updated distinction.
It has been found out that the crucial difference between induction and deduction lies on how their premises give support to their conclusion. Difference in support is measured in terms of probability or certainty. Probability pertains to a partial support, while certainty pertains to absolute support.
In an inductive argument the premises are meant to support the conclusion with probability, and this probability is dependent upon what else may be the case. Such that in a correctly structured inductive argument the conclusion is less certain than its premises. No matter how sure we are about the truth of our premises, and no matter how sure we are regarding the correctness of the argument, we simply could not guarantee a true conclusion. For instance, in this argument
we are very sure about the Mona Lisa being a work of Da Vinci and being an excellent piece of art, and so are we about the Last Supper as well as the Madonna of the Rocks. We are also sure that the argument is properly structured, and that the inference was properly made. Yet, regarding the conclusion "So probably, all works done by Da Vinci are excellent pieces of art" we just could not be sure whether it is true or false. Such a conclusion is supported by the premises only with probability. Lastly, since the probability of this conclusion is dependent upon what else may be the case, it is open to falsification once a contrary instance is cited. Hence, for instance we can cite a work by Da Vinci that is not an excellent piece of art -- in which case there are a number, for many of Da Vinci's work are not artistic but mechanical and scientific -- the conclusion is immediately established as false.
In a deductive argument, on the other hand, the premises are meant to give support to the conclusion with an absolute necessity, and this necessity is independent in any manner from whatever else may be the case. Such that in a valid deductive argument its conclusion is as certain as its premises. In the argument
the conclusion "Therefore , Bonifacio is Filipino" is as certain as the premises "Our national heroes are all Filipinos" and "Bonifacio is a national hero." Such a conclusion is supported by the premises with absolute necessity. That means if the two premises are true, then the conclusion should also be absolutely and necessarily true. Moreover, the certainty of such a conclusion is independent in any manner from whatever else may be the case. If somebody says "but some of our national heroes studied in Europe" or "Bonifacio grew in Tondo" these will in no way affect the certainty of the conclusion "Bonifacio is a Filipino."
As mentioned above, traditional logic differentiated the inductive and deductive arguments in accordance to their general movements. Inductive argument is an argument having premises that talk about particular instances, and a conclusion that talks about generalizations; and deductive argument is the reverse of that, argument having premises that talk about generalizations and a conclusion that talk about particular instances.
In the inductive argument mentioned above, the particular instances talking about the Mona Lisa, the Last Supper and the Madonna of the Rocks all prove the generalization that probably all works by Da Vinci are excellent pieces of art. The traditional definition of inductive argument applies well to our particular example. But such a traditional definition of inductive argument will prove too narrow when applied to other forms of induction. For instance the inductive form in the argument
does not move from particular instances to a generalization, but exactly the reverse from a generalization to the particular instance. Yet such an argument remains an inductive argument. This instance is sufficient enough to demonstrate that the traditional definition of inductive argument is inadequate, it could not cover all forms of induction.
In the deductive argument mentioned above, the generalization "Our national heroes are all Filipinos" is one of the bases of the particular instance "Therefore Bonifacio is a Filipino." Again for that instance, the traditional definition of deductive argument applies well. But when applied to other forms of induction, the traditional definition will again be found inadequate. The form involved in the deductive argument
does not move from a generalization to a particular instance, but from a hypothetical claim to a particular instance. Yet the argument is a valid deductive argument. This type of deductive argument together with some other forms of deduction would not fit into the very narrow traditional definition.
Hence, it is but fitting to abandon the traditional definition in favor of the more updated modern definitions.
In evaluating the soundness of arguments there are at least three binary characteristic qualities to look for, namely truth/falsehood, validity/invalidity, and cogency/uncogency
In logic, truth and falsehood are characteristic qualities that can be used to describe claims alone. That means we cannot say "this or that argument is true or false" for truth and falsehood are applicable only to claims. A claim is said to be true when it corresponds with the reality which it describes; otherwise the claim would be false. For instance the claim "Our history class is very lively" can be true only if in reality our class in history is indeed lively. If on the contrary our history class is not lively, the claim "Our history class is very lively" would be false.
If truth and falsehood are applicable only to claims and can be ascertained by comparing the claims with the outside reality, validity and invalidity are only applicable to describe arguments and can be ascertained even without going into the outside of reality. Since a deductive argument follows specific patterns (to be discussed in Chapter III), even though all its claims are false as long as it conforms to a correct deductive pattern the argument is valid. Properly speaking, validity and invalidity are applicable only to deductive arguments. Inductive arguments are evaluated as or better or worse.
One way of testing the validity of argument is through the substitutional method. This method is more of a work for the common sense than of a work of logical analysis, but nonetheless this proves very helpful in discriminating valid from invalid arguments. The method is done by substituting the contents of an unfamiliar argument with the contents of a similar but more familiar argument. For instance the argument
may not be immediately identified as valid or invalid because of our relative unfamiliarity with the terms involved. Once we substitute the terms of the argument with more familiar ones, its validity or invalidity might become visible.
With the proper substitution of the contents of the first argument, we can see clearly that it is in fact invalid. If relative unfamiliarity makes it difficult to see the validity or invalidity of a given argument, so will over-familiarity. The argument
may appear valid because we already know beforehand that the claims involved are all true. We are, so to say, over familiar with its contents. Yet if we apply the same substitutional method, by letting the argument talk about another case
we will also see clearly that the original argument is again invalid. Hence, the substitutional method is not only useful in testing the validity of arguments with unfamiliar contents, it will also serve as well in determining the validity of arguments with over-familiar contents.
Again, validity and invalidity are applicable only to deductive arguments. Inductive arguments are evaluated only as either better or worse.
It is now quite clear that truth and validity are two very different things, one applies only to parts of an argument while the other to the whole argument. For this matter there can be arguments with false claims but as a whole, valid; or the other way around, arguments with true claims but invalid. For instance, the argument
has all true claims, yet invalid; while the argument.
has all false claims, yet since its conclusion flowed correctly from the premises, it is valid. There are several possible combinations showing the relationship of truth/falsehood and validity/invalidity.
As stated earlier, in a valid deductive argument, the conclusion is as certain as its premises. So, if the premises are both true, then the conclusion should necessarily be true. For this reason, there is no valid argument with true premises but false conclusion.
If truth and falsehood are applicable only to claims, and validity and invalidity are applicable only to arguments, the terms cogency and uncogency are applicable both to claims and arguments. An argument is said to be cogent, if it satisfies two requirements: first, all the claims involved must be true, or justified, or warranted; and second, the reasoning must follow any of the correct deductive patterns.
Cogency is applicable both to deductive and inductive arguments. Inductive arguments can also be called cogent if, first, all the claims involved are likewise true, justified and warranted; second, all the available and relevant information are reasonably accounted for; and third, the inference is properly done.
As we close this chapter it would be fitting to take some retrospects regarding the things that we have examined. First, we have established that philosophy fundamentally meant the love to exercize one's curiosity and that logic was originally its tool. Second, we learned that logic is the systematic study of correct argumentation, and remains very important as a tool and as a training for coping up with the intricacies and sophistication of modern life. Third, we knew the nature as well as the structure of the argument, together with how to formulate arguments clearly using the inference indicators. Fourth, we have seen the difference between simple and compound arguments and how useful the Beardsley chart is in analyzing the structure of even the most complex of the compound arguments. Fifth, we looked into the two types of arguments, induction and deduction. And lastly, we learned to evaluate arguments through subjecting them to the analysis of truth/falsehood, validity/invalidity and cogency/uncogency.
INTRODUCING PHILOSOPHY WHAT IS LOGIC? 
LOGIC IN THE ANCIENT AND MEDIEVAL WORLDS LOGIC AND THE MODERN WORLD THINKING, REASONING AND HUMAN LIFE THE MODERN WORLD AS A REGIME OF KNOWLEDGE TRUTH IN THE INFORMATION AGE LOGIC IN THE CYBER AGE THE ARGUMENT AS THE DIRECT OBJECT OF STUDY
As defined earlier, logic is the philosophical study of human reasoning, or thinking. But, as it is obvious human reasoning or thinking are both mental processes which in themselves can easily escape any sort of direct systematic study. For this reason the study of logic is not done directly on reasoning or thinking, but on the arguments which can be considered as the audible or tangible manifestation of human reasoning or thinking. To put it more clearly, human reasoning or thinking isaccessible only through the spoken or written argument. 
WHAT IS AN ARGUMENT? THE BASIC STRUCTURE OF AN ARGUMENT






IDENTIFYING ARGUMENTS 
Therefore, next month is December.
It follows that this month is November.PRESUPPOSED PARTS, THE UNSTATED CLAIMS 
SIMPLE AND COMPOUND ARGUMENTS 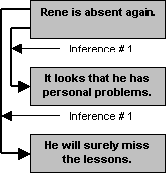
The more you know, the more you forget. The more you forget, the less you know.
The less you know, the less you learn. So, why study?![]()
![]()
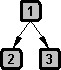
![]()
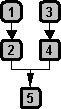
INDUCTION AND DEDUCTION MODERN DEFINITIONS
The Last Supper, by Da Vinci, is an excellent piece of art.
The Madonna of the Rocks, by Da Vinci, is an excellent piece of art.
So probably, all works done by Da Vinci are excellent pieces of art.
Bonifacio is a national hero.
Therefore, Bonifacio is a Filipino.THE INADEQUACY OF THE OLD DEFINITIONS
Tomas Reyes is a Filipino.
So probably, Tomas Reyes lives below the poverty line.
He was assassinated.
Therefore, he died.
TRUTH, VALIDITY AND COGENCY TRUTH AND FALSEHOOD 
VALIDITY AND INVALIDITY 
Slavs are Europeans.
Therefore, Slavs are people from Spain.
Singaporeans are Asians.
Therefore, Singaporeans are people from the Philippines.
Benigno Aquino, Jr. died.
Therefore, he was assassinated.
Ferdinand Marcos died.
Therefore, he was assassinated.TRUTH AND VALIDITY
Styracosaurus is an extinct species.
So, styracosaurus is a dinosaur.
Manila is in Paco.
Therefore, Philippines is in Paco.
Whales are mammals.
Therefore, whales feed their young with milk.
Michael Jordan is an African.
So, he is black skinned.
Birds are all marine creatures.
Therefore, bats are marine creatures.
That cigarette vendor surely does not own a hundred hectare rice field.
Therefore, that cigarette vendor is not rich.
Magsaysay died.
Therefore, Magsaysay was assassinated.
All Filipinos are American.
Therefore, the President of the Republic of the Philippines is a Filipino.
Students of San Beda College are not leading healthy lives.
So, they must be taking drugs in large dosage regularly.COGENCY AND UNCOGENCY 
CHAPTER SUMMARY