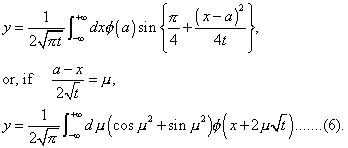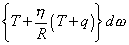, from which we find for the moment of the couple acting across the section188. When the bar, whose lateral vibrations are to be considered is subject to longitudinal tension, the potential energy of any configuration is composed of two parts, the first depending on the stiffness by which the bending is directly opposed, and the second on the reaction against the extension, which is a necessary accompaniment of the bending, when the ends are nodes. The second part is similar to the potential energy of a deflected string ; the first is of the same nature as that with which we have been occupied hitherto in this Chapter, though it is not entirely independent of the permanent tension.
Consider the extension of a filament of the bar of section dω, whose distance from the axis projected on the plane of vibration is η. Since the sections, which were normal to the axis originally, remain normal during the bending, the length of the filament bears to the corresponding element of the axis the ration R + η : R, R being the radius of curvature. Now the axis itself is extended in the ratio q : q + T, reckoning from the unstretched state, if Tω denote the whole tension to which the bar is subjected.
Hence the actual tension on the filament is 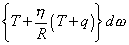, from which we find for the moment of the couple acting across the section
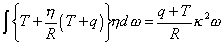
and for the whole potential energy due to stiffness
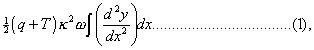
an expression differing from that previously used (§ 162) by the substitution of q + T for q.
Since q is the tension required to strech a bar of unit area to twice its natural length, it is evident that in most practical cases T would be negligable in comparison with q.
The expression (1) denotes the work that would be gained during the straightening of the bar, if the length of each element of the axis were preserved constant during the process. But when a stretched bar or string is allowed to pass from a displaced to the natural position, the length of the axis is decreased. The amount of the decrease is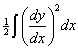 
, and the corresponding gain of work is
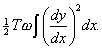
Thus
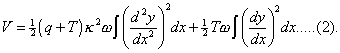
The variation of the first part due to a hypothetical displacement is given in §162. For the second part, we have
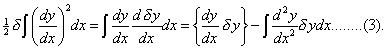
In all the cases that we have to consider, δy vanishes at the limits. The general differential equation is accordingly
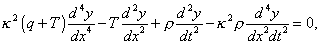
or, is we put q + T = b2ρ, T = α2ρ,
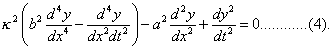
For a more detailed investigation of this equation the reader is referred the writings of Clebsch and Donkin. [Theorie de Elasticität fester Körper. Leipzig, 1862.]
189. If the ends of the rod, or wire, be clamped,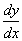 
= 0. and the terminal conditions are satisfied. If the nature of the support be such that, while the extremity is constrained to be a node, there is no couple acting on the bar, 
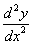must vanish, that is to say, the end must be straight. This supposition is usually taken to represent the case of a string stretched over bridges, as in many musical instruments ; but it is evident that the part beyond the bridge must partake of the vibration, and that therefore its length cannot be altogether a matter of indifference.
If in the general differential equation we take y proportional to cos nt, we get
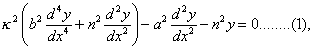
which is evidently satisfied by
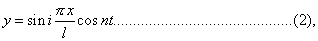
if n be suitably determined. The same solution also makes y and y'' vanish at the extremities. By substitution we obtain for n,
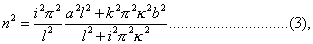
which determines the frequency.
If we suppose the wire infinitely thin, n2 = i2π2α2 ÷ l2, the same as found in Chapter VI., by starting from the supposition of perfect flexibility. If we treat κ : l as a very small quantity, the approximate value of n is
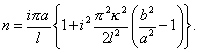
For a wire of circular section of radius r, κ = ¼ r2, and if we replace b and &alpha by their values in terms of q, T, and ρ,
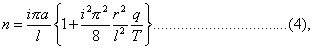
which gives the correction for rigidity [Donkin's Acoustics, Art. 184.]. Since the expression within the brackets involves i, it appears that the harmonic relation of the component tones is disturbled by the stiffness.
190. The investigation of the correction for stiffness when the ends of the wire are clamped is not so simple, in consequence the change of type which occurs near the ends. In order to pass from the case of the preceding section to that now under consider taino an additonal constraint must be introduced, with the effect of stiff further raising the pitch. The following is, in the main, the investigation of Seebeck and Donkin.
If the rotatory inertia be neglected, the differential equation becomes
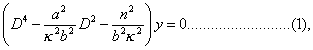
where D stands for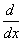 
. In the equation
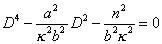
one of the values of D2 must be positive, and the other negative. We may therefore take
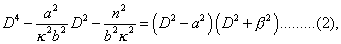
and for the complete integral of (1)
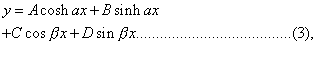
where α and β are functions of n determined by (2)
The solution must now be made to satisfy the four boundary conditions, which, as there are only three disposable ratios, lead to an equation connecting α, β, l. This may be put into the form
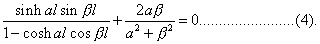
The value of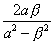 
, determined by (2), is 
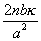, so that
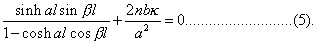
From (2) we find also that
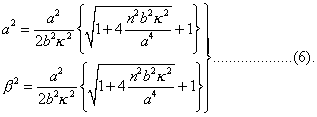
Thus far our equations are rigorous, or rather as rigorous as the differential equation on which they are founded ; but we shall now introduce the supposition that the vibration considered is but slightly affected by the existence of rigidity. This being the case, the approximate expression for y is
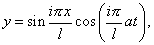
and therefore
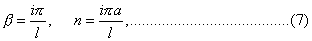
nearly.
The introduction of these values into the second of equations (6) proves that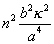 
or 
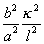is a small quantity under the circumstances contemplated, and therefore that α2l2 is a large quantity. Since cosh αl, sinh αl are both large, equation (5) reduces to
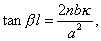
or, on substitution of the approximate value for β derived from (6),
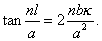
The approximate value of nl/&alpha is iπ. If we take nl/&alpha = iπ + θ, we get
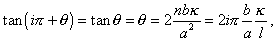
so that
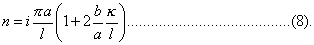
According to this equation the component tones are all raised in pitch by the same small interval, and therefore the harmonic relation is not disturbed by the rigidity. It would probably be otherwise if terms involving κ2 : l2 were retained ; it does not therefore follow that the harmonic relation is better preserved in spite of rigidity when the ends are clamped than when they are free, but only that there is no additional disturbance in the former case, though the absolute alteration of pitch is much greater, It should be remarked that b : α or √ (q + T) : √T, is a large quantity, and that, if our result is to be correct, κ : l must be small enough to bear multiplication by b : a and yet remain small.
The theoretical result embodied in (8) has been cmpared with experiment by Seebeck, who found a satisfactory agreement. The constant of stiffness was deduced from observations of the rapidity of the vibrations of a small piece of the wire, when one end was clamped in a vice.
191. It has been shewn in this chapter that the theory of bars, even when simplified to the utmost by the omission of unimportant quantities, is decidedly more complicated than that of perfectly flexible strings. The reason of the extreme simplicity of the vibrations of strings is to be found in the fact that waves of the harmonic type are propagated with a velocity independent of the wave length, so that an arbitrary wave is allowed to travel without decomposition. But when we pass from strings to bars, the constant in the differentual equation, viz.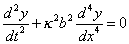 
is no longer expressible as a velocity, and therefore the velocity of transmission of a train of harmonic waves cannot depend on the differential equation alone, but must vary with the wave length. The same thing may be seen from the solution applicable to waves propagated in one direction, viz. 
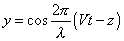, which satisfies the differential equation if
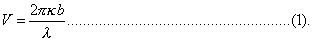
Let us suppose that there are two trains of waves of equal amplitudes, but of different wave lengths, travelling in the same direction. Thus,
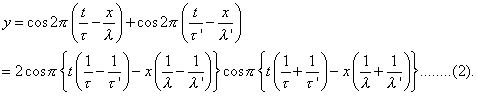
If τ' - τ, λ' - λ be small, we have a train of waves, whose amplitude slowly varies from one point to another between the values 0 and 2, forming a series of groups separated from one another by regions comparitively free from disturbance. In the case of a string or of a column of air, λ varies as τ, and then the groups move forward with the same velocity as the component trains, and there is no change of type. It is otherwise when, as in the case of a bar vibrating transversely, the velocity of propagation is a function of the wave length. The position at time t of the middle of the group which was initially at the origin is given by
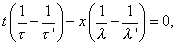
which shews that the velocity of the group is
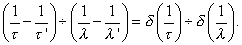
If we suppose that the velocity V of a train of waves varies as λ'', we find
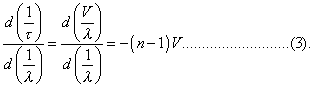
In the present case n = -1, and accordingly the velocity of the groups is twice that of the component waves.*
* In the corresponding problem for waves on the surface of deep water, the velocity of propagation varies directly as the square root of the wave length, so that n = ½. The velocity of a group of such waves is thereforeof that of the component trains.
192. On account of the dependence of the velocity of propagation on the wave length, the condition of an infinite bar at any time subsequent to an initial disturbance confined to a limited portion, will have none of the simplicity which characterized the corresponding problem for a string ; but nevertheless Fourier's investigation of this question may properly find a place here.
It is required to determine a function of x and t, so as to satisfy
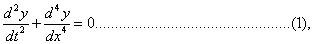
and make initially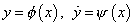 
.
A solution of (1) is
where q and α are constants, from which we conclude that
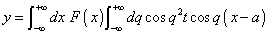
is also a solution, where F(α) is an abitrary function of α. If now we put t = 0,
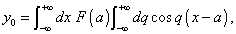
which shews that F(α) must be taken to be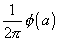 
, for then by Fourier's double integral theorem y0 = φ (x). Moreover 
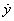= 0 ; hence
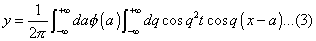
satisfies the differential equation and makes intitally,
y = &phi(x), 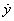= 0.
By Stokes' theorem (§ 95), or independently, we may now supply the remaining part of the solution, which has to satisfy the differential equation while it makes initially y = 0, 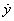= ψ (x); it is
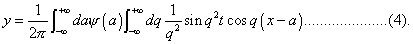
The final result is obtained by adding the right-hand members of (3) and (4).
In (3) the integration with respect to q may be effected by means of the formula
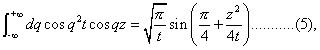
which may be proved as follows. If in the well-known integral formula
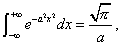
we put x + b for x we get
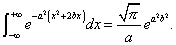
Now suppose that a2 = i = e½iπ, where i = √ -1. and retain only the real part of the equation. Thus
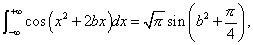
whence
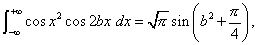
from which (5) follows by a simple change of variable. Thus equation (3) may be written
