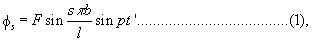
130. The problem which will next engage our attention is that of the pianoforte wire. The cause of the vibration is here the blow of a hammer, which is projected against the string, and afterwards rebounds. But we should not be justified in assuming, as in the last section, that the mutual action occupies so short a time that its duration may be neglected. Measured by the standards of ordinary life the duration of the contact is indeed very small, but here the proper comparison is with the natural periods of the string. Now the hammers used to strike the wires of a pianoforte are covered with several layers of cloth for the express purpose of making them more yielding with the effect of prolonging the contact. The rigorous treatment of the problem would be difficult, and the solution, when obtained, probably too complicated to be of use ; but by introducing a certain simplification Helmholtz has obtained a solution representing all the essential features of the case. He remarks that since the actual yielding of the string must be slight in comparison with that of the covering of the hammer, the law of the force called into play during the contact must be nearly the same as if the string were absolutely fixed, in which case the force would vary very nearly as a circular function. We shall therefore suppose that at the time t = 0, when there are neither velocities nor displacements, a force Fsin pt begins to act on the string at x = b, and continues through hald a period of the circular funtion, that is, until t = π / p, after which the string is once more free. The magnitude of p will depend on the mass and elasticity of the hammer, but not to any great extent on the velocity with which it strikes the string.
The required solution is at once obtained by substituting for φv in the general formula (7) of § 128 its value given by
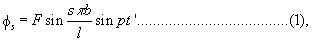
the range of the integration being from 0 to π/p. We find
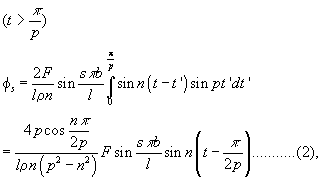
and the final solution for y becomes, if we substitute for n and ρ their values,
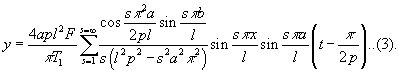
We see that all components vanish which have a node at the point of excitement , but this conclusion does not depend of any particular law of force. The interest of the present solution lies in the information that may be elicited from it as the dependence of the resulting vibrations on the duration of contact. If we denote the ratio of this quantity to the fundamental period of the string by v, so that v = π&alpha : 2 pl, the expression for the amplitude of the component s is
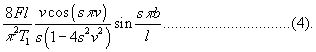
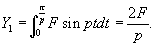
When v is finite, those components disappear, whose periods are 2/3, 2/5, 2/7, ... of the duration of contact ; and when s is very great, the series converges with s-3. Some allowance must also be made for the finite breadth of the hammmer, the effect of which will also be to favour the convergence of the series.
The laws of the vibration of strings may be verified, at least in their main features, by optical methods of observation - either with the vibration-microscope, or by a tracing point recording the character of the vibration of a revolving drum. This character depends on two things:- the mode of excitement, and the point whose motion is selected for observation. Those components do not appear which have nodes either at the point of excitement, or at the point of observation. The former are not generated, and the latter do not manifest themselves. Thus the simplest motion is obtained by plucking the string at the centre, and observing one of the points of trisection, or vice versa. In this case the first harmonic which contaminates the purity of the principal vibration is the fifth component, whose intensity is usually insufficient to produce much disturbance. ...
135. Thus far we have supposed that at two fixed points x = 0 and x = l, the string is held at rest. Since absolute fixity cannot be attained in practice, it is not without interest to inquire in what manner the vibrations of a string are liable to be modified by a yielding of the points of attachment ; and the problem will furnish occasion for one or two remarks of importance. For the sake of simplicity we shall suppose that the system is symmetrical with reference to the centre of the string, and that each extremity is attached to a mass M (treated as unextended in space), and is urged by a spring (μ) towards the position of equilibrium. If no frictional forces act, the motion is necessarily resolvable into normal vibrations. Assume
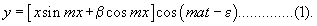
The conditions at the ends are that
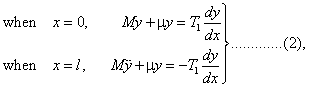
which give
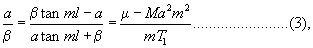
two equations, sufficient to determine m, and the ratio of β to α. Eliminating the latter ratio, we find
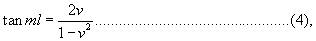
if for brevity we write v for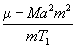 
.
Equation (3) has an infinite number of roots, which may be found by writing tan θ for v, so that tan ml = tan 2θ , and the result of adding together all the corresponding particular solutions, each with its two arbitrary constants α and ε, is necessarily the most general solution of which th eproblem is capable, and is therefore adequate to represent the motion du to an arbitrary initial distribution of displacement and velocity. We infer that any function of x may be expanded between x = 0 and x = l in a series of terms
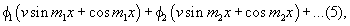
mv mx &c. being the roots of (3) and v1, v2, &c. the corresponding values of v. The quantities of &phi1, &phi2, &c. are the normal co-ordinates of the system.
From the symmetry of the system it follows that in each normal vibration the value of y is numerically the same at points equally distant from the middle of the string, for example, at the two ends, where x = 0 and x = l. Hence v0 sin m4l + cos mbl = ± 1, as may be proved also from (4)
The kinetic energy T of the whole motion is made up of the energy of the string, and that of the masses M. Thus
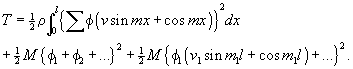
But the characteristic property of normal co-ordinates, terms containing their products cannot be really present in the espression for T, so that
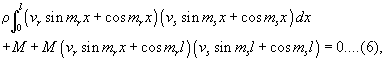
if τ and s be different.
This theorem suggests how to determine the arbitrary constatns, so that the series (5) may represent an arbitrary function y. Take the expression
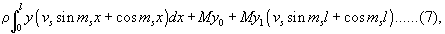
and substitute in it the series (5) expressing y. The result is a series of terms of the type
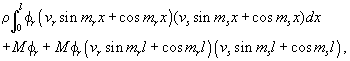
all of which vanish by (6), except the one for which τ= s. Hence φ0 is equal to the expression (7) divided by
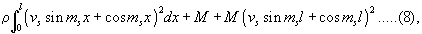
and thus the coefficients of the series are determined. If M = 0, even although μ be finite, the process is of course much simpler, but the unrestricted problem is instructive. So much stress is often laid on special proofs of Fourier's and Laplace's series, that the student is apt to acquire too contracted a view of the nature of those important results of analysis.
...
We now proceed to examine the effects of a slight yielding of the supports, in the case of a string whose ends are approximately fixed. The quantity v may be great, either through μ or through M. We shall confine ourselves to the two principal cases, (1) when μ is great and M vanishes, (2) when μ vanishes and M is great.
In the first case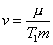 
,
and the equation in m is approximately
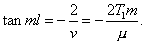
Assume ml = sπ + x, where x is small; then
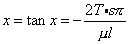approximately,
and
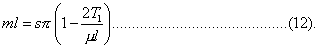
To this order of approximation the tones do not cease to form a harmonic scale, but the pitch of the whole is slightly lowered. The effect of the yielding is in fact the same as that of an increase in the length of the string in the ratio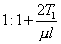 
, as might have been anticipated.
The result is otherwise if μ vanish, while M is great. Here
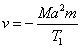
and
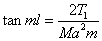approximately.
Hence
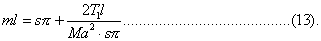
The effect is this equivalent to a decrease in l in the ratio
,
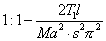and consequently there is a rise in pitch, the rise being the greater the lower the component tone. It might be thought that any kind of yielding would depress the pitch of the string, but the preceeding investigation shews that this is not the case. Whether the pitch will be raised or lowered, depends on the sign of v, and this again depends on whether the natural note of the mass M urged by the spring μ is lower or higher than that of the component vibration in question.
...
137. Actual strings and wires are not perfectly flexible. They oppose a certain resistance to bending, which may be divided into two parts, producing two distinct effects. The first is called viscosity, and shews itself by damping the vibrations. This part produces no sensible effect on the periods. The second is conservative in its character, and contributes to the potential energy of the system, with the effect of shortening the periods. A complete investigation cannot conveniently be given here, but the case which is most interestin in its application to musical instruments, admits of a sufficiently simple treatment.
When rigidity is taken into account, something more must be specified with respect to the terminal conditions than that y vanishes. Two cases may be particularly noted: -
(1) When the ends are clamped, so that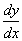 
= 0 at the ends.
(2) When the terminal directions are perfectly free, in which case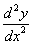 
= 0.
It is the latter which we propose now to consider.
If there were no rigidity, the type of vibration would be
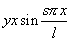, satisfying the second condition.
The effect of the rigidity might be slightly to disturb the type ; but whether such a result occur of not, the period calculated from the potential and kinetic energies on the supposition that the type remains unaltered is necessarily correct as far as the first order of small quantities ...
Now the potential energy due to the stiffness is expressed by
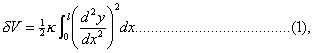
where κ is a quantity depending on the nature of the material and on the form of the section in a manner that we are not now prepared to examine. The form of δV is evident, because the force required to bend any element ds is proportional to ds, and to the amount of bending already effected, that is to ds ÷ ρ. The whole work which must be done to produce a curvature 1 ÷ ρ in ds is therefore proportional to ds ÷ ρ2; while to the application to which we work ds = dx, and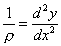 
.
Thus
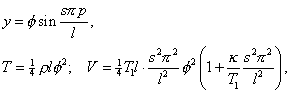
and the period of φ is given by
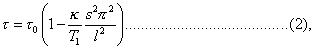
If τ0 denote what the period would become if the string were endowed with perfect flexibility. It appears that the effect of the stiffness increases rapidly with the order of the component vibrations, which cease to belong to a harmonic scale. However, in the strings employed in music, the tension is usually sufficient to reduce the influence of rigidity to insignificance.
The method of this section cannot be applied without modification to the other case of terminal condition, namely, when the ends are clamped. In their immediate neighborhood the type of vibration must differ from that assumed by a perfectly flexible string by a quantity, which is no longer small, and whose square therefore cannot be neglected. ...
...
141. The differential equation determining the motion of a string, whose longitudinal density ρ is variable, is
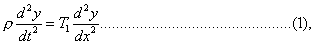
from which, if we assume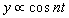 
, we obtain to determine the normal functions
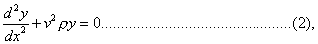
where v2 is written for n2÷T1. This equation is of the second order and linear, but has not hitherto been solved in finite terms. Considered as defining the curve assumed by the string in the normal mode under consideration, it determines the curvature at any point, and accordingly embodies a rule by which the curve can be constructed graphically. Thus in the application to a string fixed at both ends, if we start from either end at an arbitrary inclination, and with zero curvature, we are always directed by the equation with what curvature is to proceed, and in this way we may trace out the entire length.
If the assumed value of v2 be right, the curve will cross the axis of x at the required distance, and the law of vibration will be completely determined. If v2 be not known, different approximation to the value of v2 may usually be arrived at by a calculation founded on an assumed type ...
Whether the longitudinal density be uniform or not, the periodic time of any simple vibration varies coeteris paribus as the square root of the density and inversely as the square root of the tension under which the motion takes place.
The converse problem of determining the density, when the period and the type of vibration are given, is always soluble. For this purpose it is only necessary to substitute the given value of y, and of its second differential coefficient in euqation (2). Unless the density be infinite, the extremities of a string are points of zero curvature.
When a given string is shortened, every component tone is raised in pitch. For the new state of things may be regarded as derived from the old by introduction, at the proposed point of fixture, of a spring (without inertia), whose stiffness is gradually increased without limit. At each step of the process the potential energy of a given deformation is augmented, and therefore ... the pitch of every tone is raised. In like manner an addition to the length of a string depresses the pitch, even though the added part be destitute of inertia.
§ 188. Lateral Vibrations of Bars