DESSIN - Polygones réguliers et étoiles

En général, ce terme désigne les formes ayant au moins cinq côtés et beaucoup d'entre eux ont des noms spécifiques qui désignent le nombre de côtés.

Nom	Nombre de côtés	Angle au centre
Pentagone	5	72°
Hexagone	6	60°
Heptagone	7	51 3/7° ou 51,43
Octogone	8	45°
Ennéagone	9	40°
Décagone	10	36°
Hendécagone	11	32,72°
Dodécagone	12	30°

Pour d'autres polygones à plus de 12 côtés, divisez 360 par le nombre de côtés désirés.
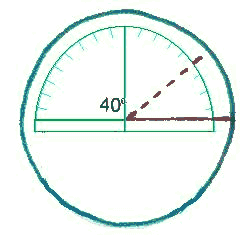
NOTE: Merci à JL Ferrari pour la correction des termes mathématiques.

Dessin d'un polygone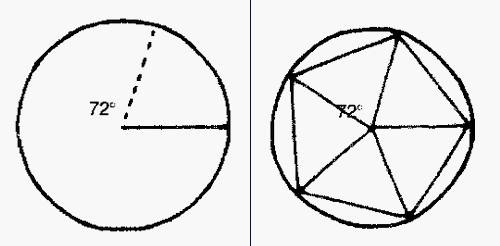

IMAGE DE GAUCHE: Tracez un cercle aux dimensions que vous désirez donner au polygone. Marquez bien le centre du cercle où se trouvait la pointe du compas et tracez un rayon. Divisez 360° par le nombre de côtés du polygone en vous guidant sur le tableau ci-dessus.

IMAGE DE DROITE: À l'aide du rapporteur, reportez cet angle qui aura pour origine le centre du cercle et pour côté le rayon déjà tracé. Le deuxième côté de l'angle coupera le cercle au sommet suivant du polygone. Répétez ce processus tout autour du cercle et joignez les sommets qui constituent le polygone.

Dans la mesure où vous avec un repère sûr pour positionner le rapporteur, il n'est pas nécessaire de tracer les rayons. Si le polygone comporte un nombre pair de côtés, il suffit de tracer les sommets sur la moitié de la circonférence; pour obtenir les sommets sur l'autre côté, vous prolongerez les rayons jusqu'à ce qu'ils coupent le cercle.

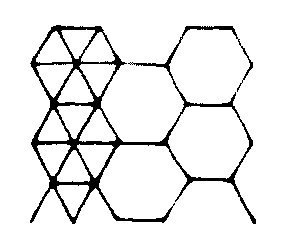
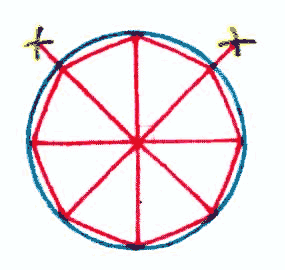
Hexagone sans rapporteur

Vous pouvez dessiner un hexagone sans rapporteur puisque le côté du triangle équilatéral est égal su rayon. Tracez un cercle. L'écartement du compas étant égal au rayon, posez la pointe sur la circonférence et faites six arcs tout autour, qui vous donneront les sommets de l'hexagone.

Les hexagones sont les polygones les plus utilisés, en dehors des triangles et de certains quadrilatères, car ils sont les seuls à s'emboîter parfaitement les uns dans les autres, comme les rayons d'une ruche. Ils sont constitués de six triangles équilatéraux, les angles au centre formés par les droites tracées à partir des points adjacents de l'hexagone mesurant 60°.

Octogones

Les octogones peuvent être assemblés avec des carrés pour créer des motifs sans vides ou réunis côte à côte pour une chaînette de bordure. Vous pouvez les dessiner sans rapporteur de deux manière:

Octogone dans un cercle
Tracez dans le cercle deux diamètres formant entre eux un angle droit. Tracez les bissectrices de ces angles pour former deux autres diamètres. En joignant les extrémités des quatre diamètres, vous obtiendrez un octogone.

Octogone dans un carré

Tracez les diagonales et marquez leur point d'intersection. L'écartement du compas doit mesurer la distance entre ce point central et les sommets du carré. Posez la pointe du compas alternativement sur chaque sommet et tracez des arcs sur les côtés adjacents. En joignant les points obtenus, vous obtiendrez un octogone.

Étoiles

On peut dessiner des étoiles à un nombre quelconque de branches à partir d'un polygone régulier.

Marquez les sommets du polygone sur un cercle et reliez les sommets et en sautant un sur deux.

S'il y a plus de six sommets, reliez-les en sautant deux sur trois ou trois sur quatre, etc. Faites des essais pour trouver la forme qui vous plaît le plus.

Pour avoir des branches plus pointues, tracez les rayons de chaque sommet et dessinez un cercle au milieu. Reliez chaque sommet aux intersections du cercle et des rayons adjacents.

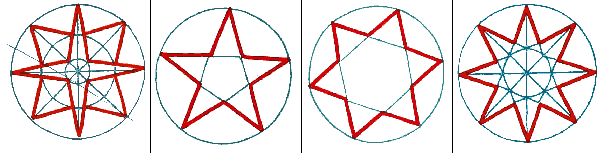
IMG 1. Avec un nombre pair de branches, on peut modifier cette méthode en traçant deux cercles intérieurs pour donner des épaisseurs différentes aux branches successives.

IMG 2. Étoile à 5 branches, dessinée à partir d'un pentagone régulier.

IMG 3. Étoile à 6 branches dessinée à partir d'un hexagone régulier.

IMG 4. Étoile à 8 branches avec des pointes effilées basées sur un cercle extérieur.

Conditions d'utilisation

Cette page fait partie du site "Artisanat pour tous". Toute utilisation à des fins commerciales, ainsi que l'archivage du site, en tout ou en partie, sont strictement interdits.

Le texte est subjectif. L'auteur ne se tient pas responsable des accidents qui pourraient subvenir en cas de négligence, des erreurs typographiques (ou de traduction), ou de la disponibilité des pages.
Tous les documents sont publiés ici uniquement pour des raisons éducatives et informatives. Aucune permission n'a été demandée ou accordée pour la diffusion, la traduction ou la modification des documents utilisés.

This is a personal site created in 1998, with monthly updates ever since. It has not be "upgraded", so, there is no interactive page, no "likes", no videos or even animations, no comments box either. So, if you want to communicate with me, please email me at the address at top of page.