DESSIN - Ovales et spirales

Dessin d'un ovale approximatif

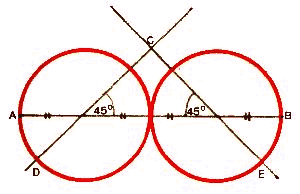	Tracez une droite représentant le plus grand axe de l'ovale qui relie les deux points opposés A et B. Placez la pointe de votre compas au quart de AB, à partir de chaque extrémité et tracez deux cercles égaux tangents au milieu de la droite AB. Tracez un angle de 45° à partir du centre de chaque cercle et marquez le point C au point de rencontre des deux droites. Prolongez celles-ci de l'autre côté de chaque cercle qu'elles coupent respectivement en D et E.
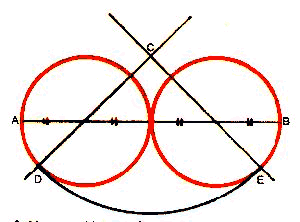	Placez la pointe du compas en C et la mine en D puis tracez l'arc DE. Recommencez l'opération pour tracer l'autre moitié de l'ovale. Dans cet ovale, la proportion du plus grand axe par rapport au plus petit (la plus grande largeur sur la plus grande hauteur) est environ de 10 sur 7.
	Pour obtenir une forme plus ronde, les angles tracés à partir des centres mesureront moins de 45° et pour une forme plus allongée, plus de 45°. Pour la suite du dessin, suivez la même méthode.

Dessin d'un ovale parfait

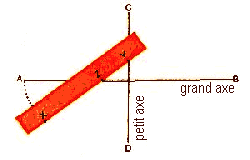Les 2 axes d'un ovale se coupent à angle droit: tracez le grand axe (AB); tracez le petit axe (CD) qui le coupe. Prenez une carte ou tout autre objet ayant un bord droit et d'une longueur au moins égale à la moitié de celle de l'axe AB. Déterminez cette moitié rapportée sur le bord droit, par les points X et Y. Marquez le point Z de telle sorte que XZ soit égale à la moitié du petit axe CD. Placez le bord de la carte sur les axes, de façon que Z soit sur le grand axe et Y sur le petit. Faites un point sur l'emplacement de X. Faites tourner la carte en laissant Z et Y sur leurs axes respectifs et faites une série de points déterminés par X. Vous obtiendrez un ovale en pointillé et vous n'avez plus qu'à joindre tous les points à main levée pour achever la forme.

Spirales

Une forme très répandue dans la nature, de nombreux mathématiciens se sont intéressés à la spirale. Sir Christopher Wren découvrit que c'était un cône enroulé sur son axe. La spirale a aussi un rapport avec la suite de Fibonacci, suite de nombres telle que chacun d'eux est la somme des deux termes immédiatement précédents: 1, 1, 2, 3, 5, 8, 13, 21, 34, etc., méthode qui sert à illustrer cette technique sur cette page. En construisant les carrés de la suite de Fibonacci, on obtient une spirale en joignant leurs centres.

Fournitures

Un carré de papier blanc de 30 cm environ
Un rapporteur d'angles
Un crayon
Une règle

Technique

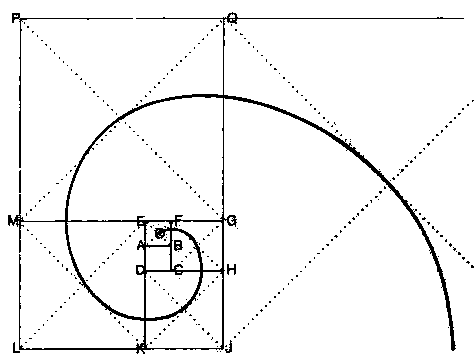
Construisez au centre de la feuille un petit carré de 6 mm de côté. Le segment AB égale une unité.
Dessinez un carré identique à ABFE ayant AB pour côté. Le point O, point d'intersection des diamètres détermine le centre.
Construisez le carré CFGH qui aura pour côté vertical gauche la ligne FBC (deux unités). Marquez-en le centre.
Construisez ensuite le carré DHJK qui aura pour côté horizontal supérieur la ligne DCH (trois unités). Marquez-en le centre.
Construisez alors le carré EKLM qui aura pour côté vertical droit la ligne EADK (5 unités). Marquez-en le centre.
Enfin, le carré MGQP aura pour côté horizontal inférieur la ligne MEFG (huit unités).
Dessinez des carrés jusqu'à ce que la feuille soit pleine.
Tracez au crayon le profil de la spirale, à partir de O, en réunissant les centres.

Spirale plus lovée

Fournitures

Un carré de carton léger d'environ 15 cm de côté
Des ciseaux.

Technique

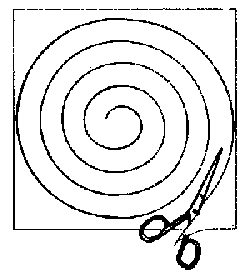
À partir d'un coin, découpez une spirale toujours plus petite en faisant des courbes régulières.
Arrivée au centre, ouvrez la spirale pour lui donner du volume.

Vous trouverez le même phénomène en pelant une pomme en continu, sans casser la peau. Celle-ci formera tout naturellement une spirale.

Cette page fait partie du site "Artisanat pour tous" © (année en cours). Toute utilisation à des fins commerciales, ainsi que l'archivage du site, en tout ou en partie, sont strictement interdits.

Le texte est subjectif. L'auteur ne se tient pas responsable des accidents qui pourraient subvenir en cas de négligence, des erreurs typographiques (ou de traduction), ou de la disponibilité des pages.
Tous les documents sont publiés ici uniquement pour des raisons éducatives et informatives. Aucune permission n'a été demandée ou accordée pour la diffusion, la traduction ou la modification des documents utilisés.