DESSIN - Cercles, arcs et angles droits
Cercles
Le diamètre d'un cercle est la distance traversant le cercle dans sa partie la plus large et le rayon est égal à la moitié du diamètre.
Fournitures
- Compas ou
- Crayon, ficelle et punaise
Technique
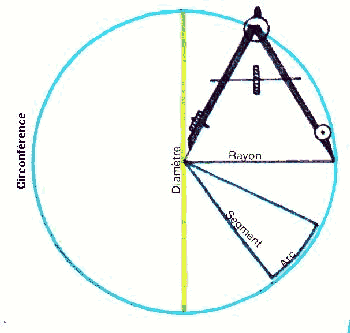 |
Pour dessiner des cercles d'un diamètre égal ou inférieur à 30 cm, servez-vous d'un compas. écartez-en les branches pour obtenir la longueur du rayon du cercle projeté. Fixez la pointe sèche à l'endroit où doit se situer le centre du cercle et laissez la pointe porte-crayon pivoter librement pour décrire un cercle parfait. Attention à conserver le compas bien droit, sinon votre trait ne finira pas exactement où il a commencé. Pour dessiner de plus grands cercles, utilisez la méthode de la ficelle de cette façon: Faites une entaille le plus près possible de la pointe d'un crayon (côté mine, pas côté gomme). Attachez-y une extrémité d'une ficelle. |
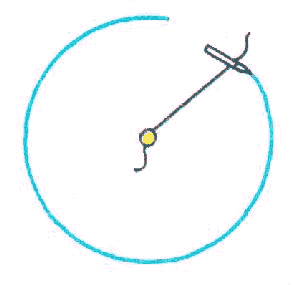 |
Enfoncez la punaise à l'autre extrémité de la ficelle pour définir exactement le rayon du cercle. Le rayon sera la distance entre la mine du crayon et la pointe de la punaise. Il n'est pas absolument nécessaire que la ficelle soit de la même longueur; si elle est trop courte, recommencez. Vous ne pourrez rien faire de convenable s'il vous manque un bout de ficelle. Si elle est franchement trop longue, coupez-en un bout ou enroulez-la sur elle-même. L'important est que la ficelle en trop ne vous nuise pas. En maintenant fermement la punaise avec le pouce (le gauche pour les droitiers et vice versa), tendez la ficelle et, en maintenant le crayon très droit, dessinez le cercle en tournant autour de la punaise, tout en gardant la même tension sur la ficelle. |
N'oubliez pas de mettre un carton ou une bonne épaisseur de journaux sous votre papier, pour empêcher la punaise de traverser votre feuille à dessin et de faire un petit trou dans la table. N'importe quel papier lisse fera l'affaire pour protéger la table, pas d'enveloppes avec des plis ou des papiers froissés, votre cercle en souffrirait.
Pour trouver la circonférence d'un cercle (Sortez vos calculatrices!), utilisez la formule: C=2xpiR, R étant le rayon et pi égale 3,1416 ou 22/7. Donc, pour un rayon de 14 cm, C=2x22/7x14 = 66 cm.
(Je sais, pi s'écrit habituellement avec un symbole qui ressemble à un drôle de petit r, mais je ne l'ai pas trouvé sur mon clavier, et je n'étais pas certaine qu'il se convertirait pour le web. Désolée.)
Arcs
Les modèles peuvent aussi contenir des arcs, c'est-à-dire des sections de cercles. Tracez une ligne horizontale et, en vous servant d'un compas (ou ficelle, crayon et punaise), dessinez une série de demi-cercles tangents sur la ligne horizontale.
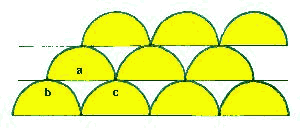 |
Tracez une ligne au sommet des demi-cercles et marquez le point A à demie distance entre B et C. En gardant le même rayon, placez la pointe du compas au point A et tracez un demi-cercle passant par b et c. Répétez tout au long du motif pour former le deuxième rang. Continuez rang après rang jusqu'à l'obtention des dimensions voulues. |
Angles droits
Bien des motifs nécessitent des rectangles parfaits et pour être assemblés avec précision, ces rectangles devront avoir des coins à angle droits (90°).
Fournitures
- Compas (ou ficelle, crayon et punaise)
- Règle ou mètre ruban rigide (galon à mesurer en métal)
Technique
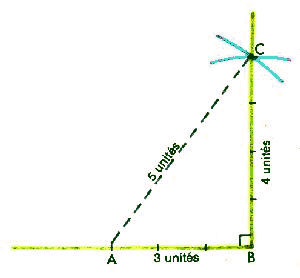 |
Tracez une ligne horizontale qui sera le premier des côtés de l'angle droit. Déterminez un point A à une distance de trois unités. Plus vos unités seront grandes et plus ce sera facile à calculer. Écartez votre compas de cinq unités ou donnez cette longueur à votre ficelle. Placez la pointe en A et dessinez un arc. Écartez maintenant votre compas de quatre unités, placez la pointe en B et dessinez un deuxième arc coupant le premier au point d'intersection C. La ligne BC sera perpendiculaire à la ligne AB. L'angle droit s'indique généralement par un petit carré, comme sur le diagramme. Cette méthode repose sur le fait que tout triangle dont les côtés ont un rapport 3-4-5 est un triangle rectangle, dont l'angle droit est compris entre les deux petits côtés. |
Conditions d'utilisation
Cette page fait partie du site "Artisanat pour tous". Toute utilisation à des fins commerciales, ainsi que l'archivage du site, en tout ou en partie, sont strictement interdits.
Le texte est subjectif. L'auteur ne se tient pas responsable des accidents qui pourraient subvenir en cas de négligence, des erreurs typographiques (ou de traduction), ou de la disponibilité des pages.
Tous les documents sont publiés ici uniquement pour des raisons éducatives et informatives. Aucune permission n'a été demandée ou accordée pour la diffusion, la traduction ou la modification des documents utilisés.
This is a personal site created in 1998, with monthly updates ever since. It has not be "upgraded", so, there is no interactive page, no "likes", no videos or even animations, no comments box either. So, if you want to communicate with me, please email me at the address at top of page.
|
|