CONSTRUCTING A

H  E  P  T  A  G  O  N

The most baffling shape in all Geometry.
By Robin Hu

Construction Number One

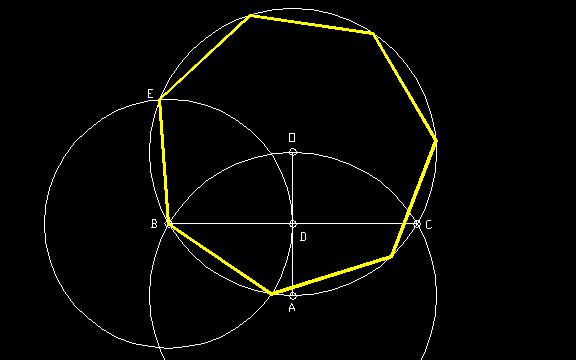
Step 1: Draw an arbitrary circle centered at O. Draw OA, the radius of circle O.
Step 2: Draw a circle centered at A with a radius of length AO. Circle A intersects the original
circle at points B and C.
Step 3: Draw a line through BC.Lines OA and BC intersect at D.
Step 4: Draw a circle centered at B with a radius of BD. This circle intersects circle O at E.
Step 5: BE is a side of the Heptagon, use it to find the others.

Out of all the constructions, in my opinion, this first one is the most easiest and most accurate. Amazingly, this construction can only be found on My website. If you bisect one of the sides, you can create an approximation for a 14-gon.

Construction Number Two

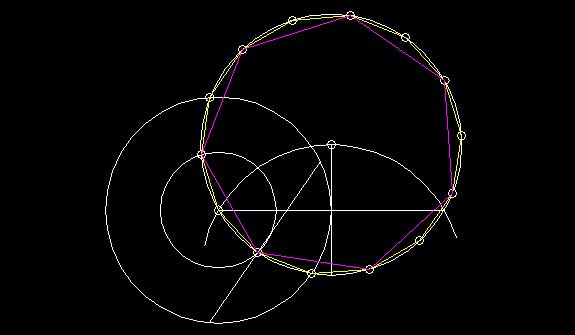
Step 1: Draw a circle A. Draw segments AB and AC so that AB is perpendicular to AC.
Draw a line through BC.
Step 2: Draw line BD so that BC is perpendicular to BD and BD is one half of BC.
Step 3: Draw a line through DC. Draw a circle at D with radius DB. Circle D intersects DC at E.
Step 4: Draw a circle at point C with radius CE. This circle intersects the original circle at two points of the heptagon.

This construction on the other hand, was actually invented by me. I found it by taking the Golden Mean of a side of square. Quite accurate for an amatuer construction.

Construction Number Three

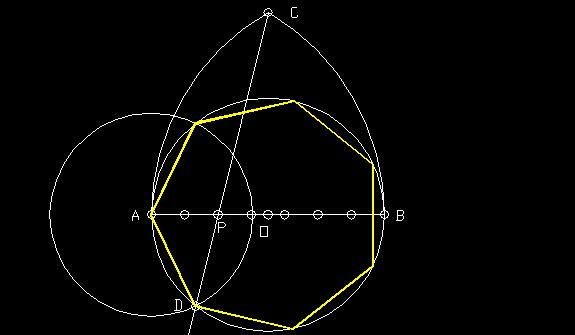
Step 1: Draw circle O with diameter AB drawn across it.
Step 2: Divide AB into 7 equal parts. Call the second point from the left P.
Step 3: Draw two circles, one centered at A and one centered at B.Both circles should have a radius of diameter AB. The two circles intersect at C.
Step 4: Draw a line through CP. Line CP intersects circle O at D. AD is a side of the heptagon.

This construction is actually based on the construction of an n-gon.

Construction Number Four

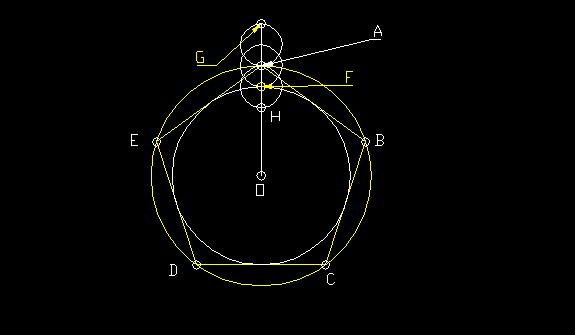
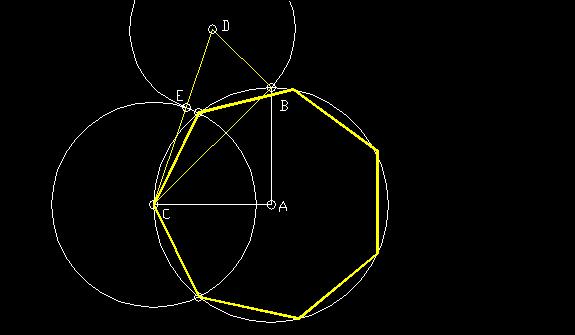
Step 1: Draw circle O. Inscribe a pentagon ABCDE inside circle O.
Step 2: Draw a circle inside of the pentagon, tangent to all sides of the pentagon (Find the midpoint M of AB and draw a circle at O with radius OM).
Step 3: Draw a line through OA. OA intersects the tangent circle at F. Draw a circle at F with radius FA. Circle F intersects line OA at H.
Step 4: Draw a circle at A with a radius of AH or copy the length of AF twice over line OA. AG is twice the length of AF.

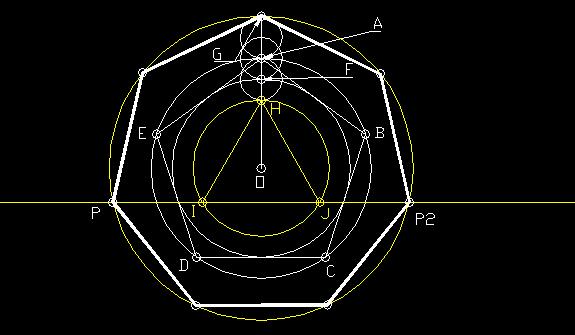
Step 5: Draw a circle at O with radius OH. Inscribe an equilateral triangle HIJ within this circle. Draw a line through IJ.
Step 6: Draw a circle at O with a radius of OG. This large circle intersects line IJ at points P and P2.
Step 7: Points G,P, and P2 are points of the heptagon.

See the NexusJournal website for more details.

NEW!!!

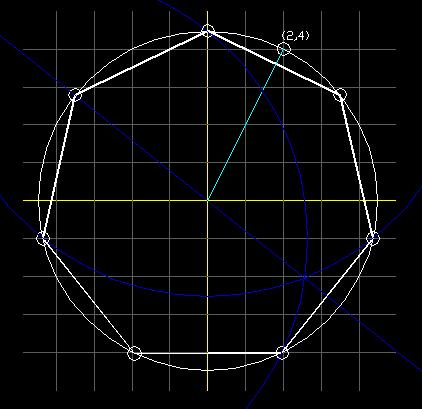
I have included a new, and totally different construction for the heptagon. It involves the use of an equally spaced x-y grid.
It's very simple. Draw a circle, with the center (0,0) and intersecting the point (2,4) and (-2,4) on the grid. Make one of the points of the heptagon the point where the circle intersects the y-axis. Then, where the line y= -1 intersects the circle, draw two more points. There are now three points of the heptagon. You can now find the other 4 points easily.

Angle Errors

Construction	Angle Measure	Percent Error
Regular Heptagon	51.428571°	0.000%
Construction #1	51.317812°	0.215%
Construction #2	51.827292°	0.775%
Construction #3	51.518222°	0.174%
Construction #4	51.460483°	0.062%
Construction #5	51.4605°	0.062%

TOP OF PAGE
Email me if you have questions or comments.

More Pages

Square	Triangle and Hexagon	Pentagon	Golden Ratio	Nonagon
Pentadecagon	Heptadecagon	N-Gon	Squaring a Circle	Basic Constructions

Click to change background

Visitor Record

Visitor Mark	Date Passed
800	10/20/2002
1000	11/1/02

This site has won the:

© 2001-2002 Robin Hu