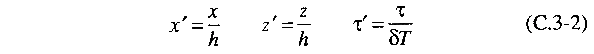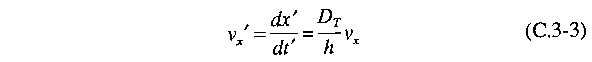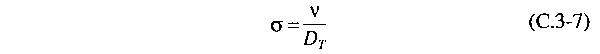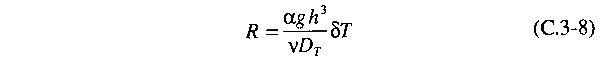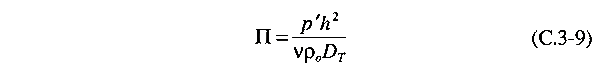|
C.3
Dimensionless Variables
Versão
em Português
Our
next step in the development of the Lorenz model is to express
the Navier-Stokes equations Eq. (C.2-11) in terms of dimensionless
variables. By using dimensionless variables, we can see which
combinations of parameters are important in determining the
behavior of the system. In addition, we generally remove the
dependence on specific numerical values of the height h
and temperature difference δT, and so on,
thereby simplifying the eventual numerical solution of the
equations.
First,
we introduce a dimensionless time variable t'
[You should
recall from Eq. (C.1-3) (and from Chapter 11) that h2/Dt
is a typical time for thermal diffusion over the
distance h.] In a similar fashion, we introduce
dimensionless distance variables and a dimensionless temperature
variable:
We can also
define a dimensionless velocity using the dimensionless distance
and dimensionless time variables. For example, the x component
of the dimensionless velocity is
Finally, the
Laplacian operator can also be expressed in terms of the new
variables with the replacement
If we use
these new variables in the Navier-Stokes equations (C.2-11)
and multiply through by h3/(vDT),
we arrive at
We
recognize that certain dimensionless ratios of parameters
appear in the equations. First, the Prandtl number
σ gives the ratio of kinematic viscosity
to the thermal diffusion coefficient:
The Prandtl
number measures the relative importance of viscosity dissipation
of mechanical energy due to the shearing of the fluid flow)
compared to thermal diffusion, the dissipation of energy by
thermal energy (heat) flow. The Prandtl number is about equal
to 7 for water at room temperature.
The Rayleigh
number R tells us the balance between the tendency
for a packet of fluid to rise due to the buoyant force associated
with thermal expansion relative to the dissipation of energy
due to viscosity and thermal diffusion. R is defined
as the combination
The Rayleigh
number is a dimensionless measure of the temperature difference
between the bottom and top of the cell. In most Rayleigh-Bénard
experiments, the Rayleigh number is the control parameter,
which we adjust by changing that temperature difference.
Finally,
we introduce a dimensionless pressure variable Π defined
as
We now use
all these dimensionless quantities to write the Navier-Stokes
equations and the thermal diffusion equation in the following
form, in which, for the sake of simpler typesetting, we have
dropped the primes (but we remember that all the variables
are dimensionless):
We should point
out that in introducing the dimensionless variables and dimensionless
parameters, we have not changed the physics content of the
equations, nor have we introduced any mathematical approximations.
|