Demonstration

In this page we will prove that we cannot switch two corners in the two-generator i.e. by turning only two (adjacent) sides of the cube. We can use this demonstration to show that for example getting into the two-generator group when solving the cube means that the corners of the LL will always be correctly placed.

(I always use "we" instead of "I" in mathematical demonstrations. I like it better because it might seem that the reader participates in the demonstration so he understands it better. But probaly the reason is that I just like it.)

The demonstration

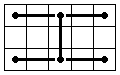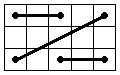
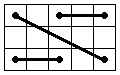
We'll use the same drawing of the two-generator as in my other pages. This time we'll focus only on the corners. We'll "connect" the corners in pairs, thus getting three "connections". The connections are between the pieces, not between their places, so they can move together with the corners. The demonstration is based on the patterns of these connections. Let's connect the corners as in the picture. The only possible positions of the connections (we don't care what the position of the corners of one pair is, i.e. they may be switched) are the ones in the pictures below (3 without symmetries, 5 with). It's easy to see that these are the only positions, but if you want to be sure you can take each position and do all possible moves, and you'll see you get one of the 5 positions. For example, by doing R' in the position 2a we will reach the position 3b.

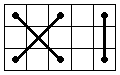
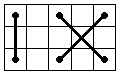
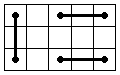Now let's try to switch two corners, for example UFR and DFR. We'll take the position 2b and we'll switch UFR and DFR. The connections' position has changed and does not make part of the 5 above shown positions (see picture). This means that from the solved position with UFR and DFR switched we can't get into the group of those positions, one of them being the solved position, so we can't switch the UFR and DFR corners. If we could switch two other corners X and Y, then bringing UFR and DFR in X and Y we could switch too UFR and DFR, which is not possible. So we cannot switch two corners in the two-generator.

How I got it

I had the idea of this demonstration (also) after I saw Charlie Tsai's page, where he said he didn't know why the permutation didn't change. This motivated me so I started to look for one (another reason was to prove I'm a good mathematician). I thought I found it so I e-mailed Charlie to tell him I have the demonstration (this happenned in June 2004) and that I will post it on my site as soon as possible. I soon found it was wrong, so I started to look for another one. This time I tried to prove that (shortly) you need an even number of moves to switch two corners, which is not possible because the permutation is odd. I thought I had found it so on about 20th of July 2004 I e-mailed him again to tell him that now I really have it. When I started writing it on computer, I found this was wrong (or rather incomplete) too. On 4th of August I really finished it and now (10th of August) I have posted it on the web.

I got the idea of connecting the corners when I noticed that switching two corners has the effect of switching two other corners, depending on the connection shown above (for example, switching UFR and DFR with UFL and UBR in their correct positions has the effect of switching DFL and DBR - from the type 1 connection). I first tried to show that you always have to switch an even number (0 or 2) of corners in a pair, but then I had the great idea that you can try switching two corners not making a pair. After that it was easy. Anyway I spent much time on thinking at this: when I didn't know what to do or I was bored, I said, let's prove you can't switch two corners in the two-generator. But now it's over.