Invariant
Mass
Back
to Physics World
Back to Special Relativity
Invariant
Mass of a Single Particle
Consider a particle with
mass m and momentum p =mv.
It can be shown that the quantity, known as the particles 4-momentum
![]()
is a 4-vector.
The inertial
energy, E, defined as the sum of the particle’s kinetic energy, K,
and it’s rest energy E0
is given by
![]()
Note; E does not
include the potential energy associate with the objects position in space. Eq.
(1) can now be expressed in terms of E
![]()
If
the particle is a tardyon (i.e. a particle that always moves at a speed
less than the speed of light) then the mass is related to proper mass m0,
(aka rest mass), as m = gm0c2.
The momentum, p, can then be written as p = mv = gm0v.
The particle’s 4-velocity, U, is defined in terms of the
particle’s spacetime displacement, dX = (cdt, dx, dy,
dz), between two events along its worldline, in terms of the proper time, dt,
between the same events. Noting that g
= dt/dt, the
4-momentum becomes
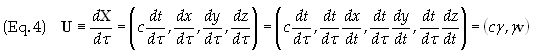
it’s readily shown that
the magnitude of U, is c2.
I.e. U·U
= c2.
Evaluating the magnitude in the rest frame of the particle one readily sees that
v = 0 and g
= 1 leaving the magnitude equal the square of the time component, c. If U
is multiplied by the particle’s proper mass then we have the equality
![]()
The magnitude, P,
of the particles 4-momentum is
![]()
Since m0
is an inherent property of a particle and the magnitude of the 4-momentum is a
Lorentz invariant, proper mass is sometimes referred to as invariant mass
since the proper mass is proportional to an invariant quantity, P.
If
the particle is a luxon, (i.e. a particle that only travels at the speed
of light) then the free-particle energy is related to the particle’s momentum
according to the relation
![]()
The magnitude of the
luxon’s 4-momentum is therefore
![]()
Thus the invariant mass of
a luxon is zero. Since photons are luxons it is said that photons have zero rest
mass.
Invariant Mass of a System of Particles - Closed
System
Consider an inertial frame
of reference in which there is a system of particles that interact only through
contact forces. It is assumed that no external forces act on any particle
included in the system – that is to say that the system is a closed system.
Since the particles only interact through contact forces it follows that
in-between collisions the worldlines of all the particles in the system are
straight. As an example consider the case of two particles, a and b,
each of which moves on a straight worldline and collide at the point of
intersection of their two worldlines as shown below in Fig. 1.
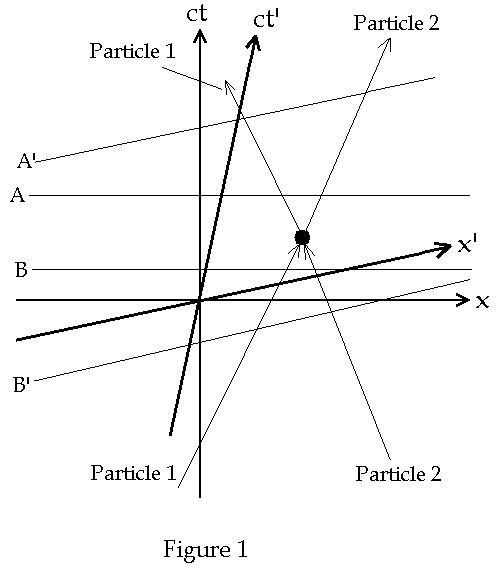
After the collision each
particle once again moves on a straight worldline. According to the laws of
conservation of mass (or energy if you prefer) and momentum, then sum of the
masses of each particle before the collision must equal the sum of the masses
after the collision, i.e.
![]()
The same holds true for
the momentum
![]()
The sum of the 4-momenta
of each particle
![]()
is also a 4-vector called
the total 4-momentum. That this is a 4-vector follows from the linearity
of the 4-vector transformation. The components of the total 4-momenta are
conserved quantities, i.e. they’re the same before and after the collision.
Thus the magnitude of the total 4-momentum is a conserved quantity. The same
holds true for the magnitude of each individual particle since the magnitude is
proportional the particle's proper mass, and inherent property, and not on the
values on the components. Since there is only one event, before and
after is well defined. This motives the following definition for the
total 4-momentum of a system of N particles
The quantity
![]()
is the invariant mass of
the system and is a conserved quantity when the particles interact only through
contact forces and is a well-defined quantity.
Implicit in the notion of
mass and momentum conservation is that one measures the mass and momentum of
each particle at the same time. An observer in S decides to measure the
total mass and momentum both before and after the collision. Lines parallel to
the axis are lines of simultaneity which means that each point on such a line,
corresponding to different events, has the same time value.
Referring to Fig. 1 the line B is a line of simultaneity, for
observers in S, corresponding to events before the collision as
observed in S. Line A is the line of simultaneity corresponding to
events after the collision for observers in S. The event at the
intersection of the line of simultaneity and the worldline of the particle is
the event at which the observer evaluates the particles 4-mometum. Since the
total momentum is conserved it makes no difference which line of simultaneity is
used so long as it doesn’t cross through the collision event. These arguments
hold for observers in frame S as well. What should be noticed at this stage is
that a line of simultaneity in S’ cannot pass through the same two
events in which observers in S and S’ chose to evaluate the
total 4-momentum. However in the present case this distinction is irrelevant.
If the particles interact
other than contact forces then the sum of the 4-momentum of the particles is not
constant, seemingly violating the conservation laws of mass and momentum.
However including the energy and momentum of the fields through which the
particles interact compensates for this violation. The fields thus have both
mass and momentum!
To summarize, the total
4-momentum of a closed system has the same transformation properties as a single
particle having the same total mass and same total momentum of the system.
Invariant Mass of a System of Particles - Non-Closed
System
In the previous section it
was assumed that the system was closed in that no external forces acts on any
particle within the system, although the particles exert forces on each other.
Lifting this restriction we now consider a case in which external forces are
acting on particles in the system. As an example we consider an inertial frame
of reference in which there is a uniform magnetic field B = Bez
aligned in the +z direction. There are two positively charged particles,
Particle 1 and Particle 2, of equal proper mass moving in the z = 0
plane. Each is given the same amount of energy and therefore they will have the
same speed. The speed, and thus the mass, of each particle is the same and
remain constant. As such their spatial trajectories are circles. We can choose
initial conditions such that the particles move in the same circle as shown in
Fig. 2.
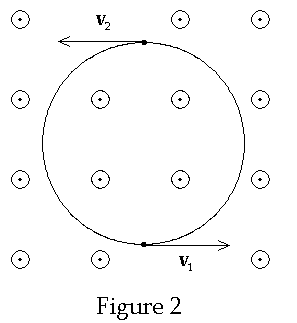
The charges are far enough
apart so that their mutual interaction can be ignored. For purposes of
illustration the energy lost through radiation will be ignored as well. The
motion is such the momentum of one particle is equal and opposite the momentum
of the other. Thus the total momentum remains zero at all times and is therefore
conserved. Since the speed of each particle is constant the total mass is
conserved as well. This situation can be achieved if the particles orbits are
180 degrees out of phase. The radius of each circle is given by the cyclotron
formula r = p/qB = gm0vc2/qB.
The position vector of particle 1 is given by
![]()
The position vector for
particle 2 is
![]()
The velocities are found
by differentiating Eqs. (14) and (15) yielding

The corresponding momenta
are found my multiplying Eq. (16) by m to give
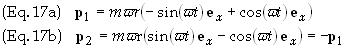
This verifies that the
total momentum vanishes. Frame S is the zero-momentum frame. Now
consider the worldlines of these particles. The x components of each
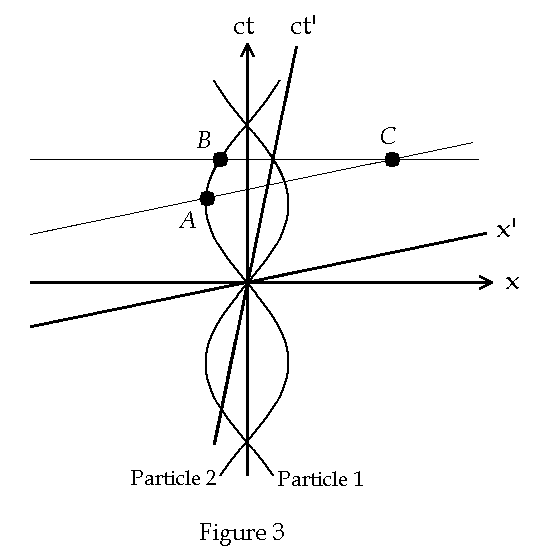
particle are shown on the spacetime diagram in Fig. 3.
The 4-momentum of each
particle varies along its worldline. The 4-momentum can parameterized by the
particle’s proper time, i.e. P = P(t).
Since the velocity varies from event to event along Particle 1’s worldline it
follows that the 4-momentum of Particle 1 also varies from event to event. It
can readily be seen from Fig. 1 that the 4-momenta of Particle 1 has a different
value at event A than it does at event C corresponding to
different values of Particle 1’s proper time. Suppose an observer in S
wants to measure the 4-momentum of both particles. The observer in S
measures the mass and momentum of Particle 1 at the same time as he
measures the mass and momentum of Particle 2. At the same time for
observers in S correspond to lines of simultaneity such as the one
connecting events B and C shown in Fig. 3. Each event along BC
has the same time coordinate and is therefore parallel to the x-axis.
Observers in S then form the 4-momenta for each particle. Let tA,
tB
and tC
are the proper times corresponding to particle 1 being at event A and
particle 2 being at event B and particle 1 being present at event C
respectively. They are
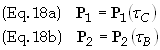
Observers in S then
decide that the want to add these 4-momenta which yields
![]()
Now consider the same
situation but from the point of view of observers in S’ who measure the
mass and momentum along the line of simultaneity AC. Observers in S’
will add these 4-momenta to form the sum
![]()
These sums are also
4-vectors. However since P2(tA)
¹
P1(tB)
it follows that
![]()
Therefore each observer
finds different values for the sum of 4-momenta. I.e. I then follows that the
magnitudes are different even though total mass and momentum are constant in
frame S.
![]()
This holds true for all
inertial observers. It follows that while the total 4-momentum of a system of
particles, which is not closed, is still a 4-vector the invariant mass is not a
physically meaningful quantity.
Invariant vs.
Time Independent
The term invariant
is sometimes confused with the time independent. These are very different
concepts. The proper mass of a particle can be both invariant and time
dependant. Consider a particle moving along an arbitrary world line. As shown in
Fig. 4 below
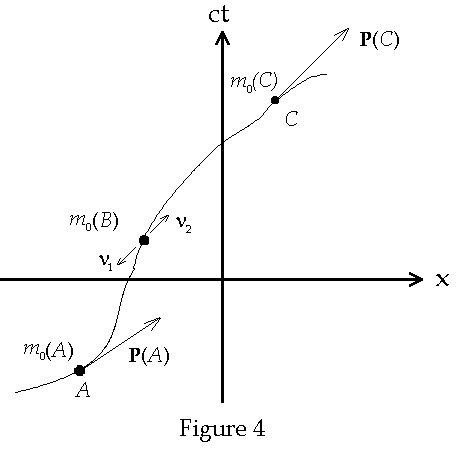
The rest mass of the
particle whose 4-momentum at event A is P(A), is m0(A)
where
![]()
As a result of the
emission of the two photons the proper mass of the photon decreases. If the
frequency of the photons in the rest frame of the particle at isn
then, according the mass-energy relation the rest mass must decrease, in this
case by the amount
![]()
Therefore the proper mass
of the particle at event B is m0(B)
where
![]()
The proper mass is now
related to the 4-momentum P(B) at event B as
![]()
This is what is meant when
it is said that proper mass is invariant and time dependant.
An Incorrect Application of Proper Invariant Mass
All of the above arguments
pertain to object whose dimensions can be ignored. Such is not always the case.
In general no invariant mass can be assigned to a macroscopic, spatially
extended, body. This is especially if the proper mass of the body is a function
of time. For example: Consider a rod, which is lying on the x-axis in the
S system. The body uniformly radiates a finite amount of energy at a
specific (short) time and over its entire length. See Fig. 5 below

The rod is drawn in
sections. Each section is colored as either red or blue, which represents the
rest energy of that section of the rod. Red represents a higher rest energy than
blue. Thus the color represents thermal energy and thus the mass of the given
section of the rod. The transition from red to blue represents cooling. Thus the
two colors of the rod represents to different states of the body and thus two
different proper masses. Now consider this from the system S’ which is
moving in the +x-direction with speed v. The sections are still
cooling but at different times. See Fig. 6 below.
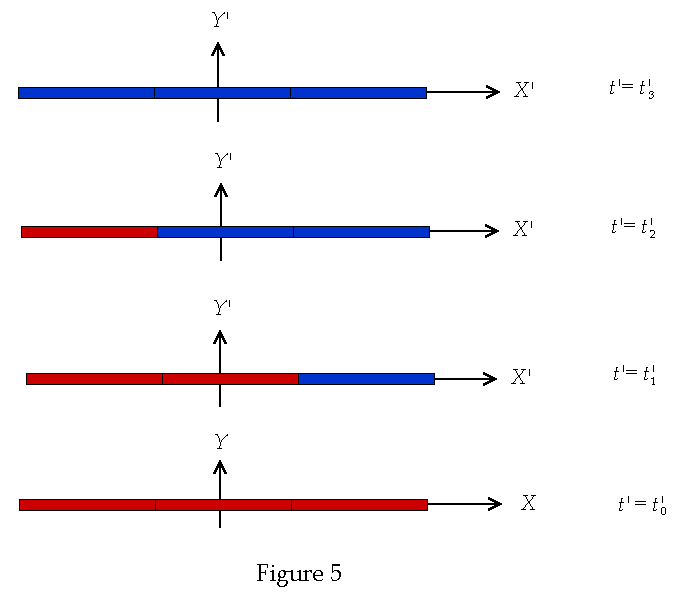
As seen from this figure,
what were simultaneous “cooling” events in S are no longer
simultaneous “cooling events” in S’ since Lorentz transformations
do not preserver simultaneity. While a well-defined proper mass can be defined
in S the same cannot be said of the rod in S’.
For this reason Eq. (5) is not meaningful since there is no unique value
of proper mass since there are many events to be considered here and not simply
one. The equations for mass, proper mass, and energy
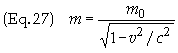
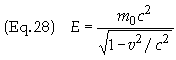
are no longer meaningful.
The relation that defines mass, i.e.
![]()
is still well defined.