Cyclotrons

Back to Physics World
Back to Special Relativity

Problem: Consider the magnetic field defined by B = B e_z (B = constant). Find the trajectory (ignoring radiation effects) of a charged particle whose initial velocity has no z-component and thus initially lies in the xy-plane. I.e. z (t = 0) = 0. Find the trajectory.

Solution:

The Lorentz force gives the force on a charged particle moving through an electromagnetic field. This force is defined by

Since E = 0 Eq. (1) reduces to

Since v´B is perpendicular to v it follows that (v´B)·v = 0. The work-energy theorem states that the work done on a particle equals the change in particle’s kinetic energy K, i.e. dW = F·dr = dK and therefore dW = F·dr Þ dK/dt = F·(dr/dt) = F·v. Substituting this into Eq. (2) gives

The kinetic energy is thus a constant of motion thus is also constant and therefore dg/dt = 0. Constant g implies the particle’s speed v = |v| is also constant. Since the B field is in the +z direction and the initial velocity is in the xy-plane it follows that the force on the particle has no +z component. The particle thus remains in the xy-plane for the entire trajectory. This situation is shown in Fig. 1 below where cylindrical coordinates are used.

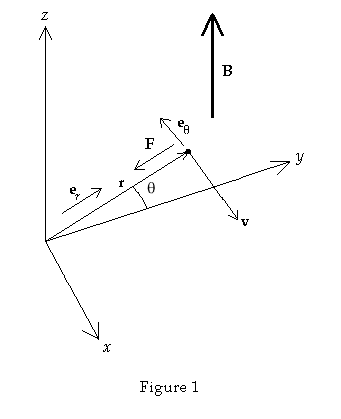
The origin of the coordinate system is defined such that the position vector r is perpendicular to the velocity. In Fig. 1 the particle is shown as a black dot at the tail of the velocity vector. The unit vectors for cylindrical coordinates are also shown. It is easy to see that the Lorentz force lies perpendicular to both the magnetic field and the velocity. The distance from the particle r is a parameter to be determined below. The figure has been drawn such that the origin lies in the direction of the force. The torque N is defined as

The angular momentum of the particle L is defined as

It can be shown that the  

According to the diagram r´F = 0 and therefore N = 0. An explicit calculation of N shows that

The velocity vector is given by

e_r and e_q are shown in Figure 1 above.  Substituting this into Eq. (7) yields 

Substitute e_r ´ e_z = - e_q and e_q ´ e_z to obtain 

Since N = 0 and r ¹ 0 it follows that  Þ r = R = constant. We now have our first integral of motion. Since the speed is constant it follow from Eq. (8) that

Since both the speed v and distance r are constant it follows that angular velocity  is also constant. Constant r and constant w means that the trajectory is a circle. From the diagram it is easy to see that a positive charge q moves in a clockwise motion around the circle. w is known as the cyclotron frequency. To find an explicit expression for w we start with the expression for the magnitude of the Lorentz force which is F = qvB. Since the motion is transverse to the acceleration we also have F = ma = mrw2 = m(rw)w = mvw = qvB . Solving for w gives w= qB/m. Therefore since v = rw then r = v/ w = p/qB.

The momentum is easily derived. The force can be calculated by noting that dp » pdq as shown in the diagram below in Figure 2.

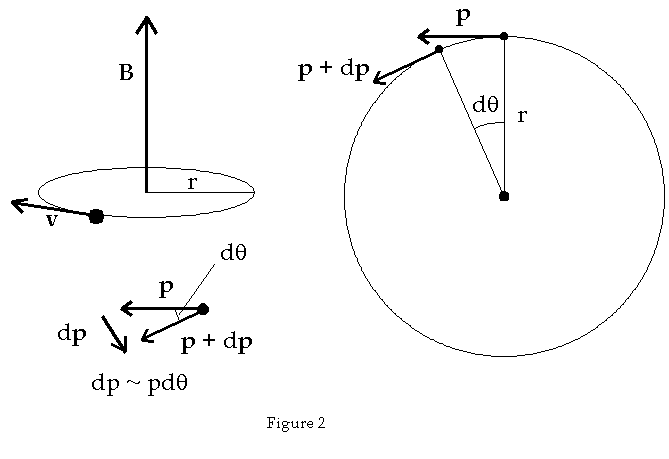
The force has a constant magnitude of F = qvB0. Substituted into Eq. (12) gives

Solving for p gives the final answer, identical to Eq. (11) as it must be. i.e. p = qB0r.

Back to Special Relativity
Back to Physics World