Conservation of Mass 

Back to Physics World
Back to Special Relativity

The 4-momentum, P, of a particle is defined in terms of the particle’s proper mass, m₀, and its 4-velocity, U º dX/dt º (cg, gv) where g º dt/dt, as

m = gm₀ is the particle’s inertial mass and p is the particle’s 3-momentum. Note that according to this P⁰ º mc. Postulate that 3-momentum is conserved in all inertial frames of reference. Let there be a system of N particles going into a collision and P particles coming out of that collision. Let us also assume that the particles interact only within a small region of space and be non-interacting otherwise. 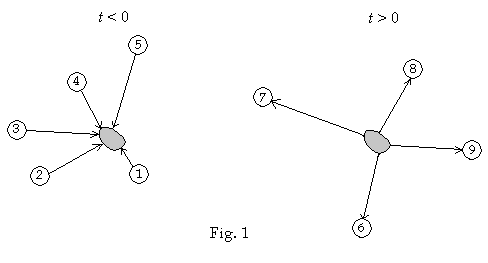Let the N particles going into the reaction be labeled 1, 2, 3, …, N and the P particles coming out of the reaction labeled N+1, N+2, … , N+P See Figure 1 below for the case N= 5 and P = 4. The shaded portion in the diagram is the only region of space where the particles interact significantly. 

Let frame S and S’ be in standard configuration where S’ is moving in the +x direction relative to S. In the notation above the expression for the conservation of each component of a particle’s linear 3-momentum is 

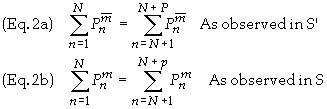
If we substitute the Lorentz transformation, given by (Note that Einstein’s summation convention is employed here).

into Eq. (2a) we obtain

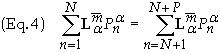
Expanding both sides we get

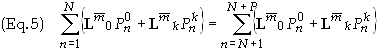
Eq. (5) can be expanded further to yield

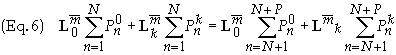
Rearranging terms and using the identity  we obtain

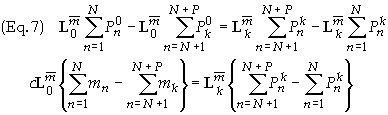
The right hand side of Eq. (7) vanishes according to Eq. (2b). Since this relationship must hold for all Lorentz transformations then this implies that the term within the parentheses on the left hand since must vanish giving

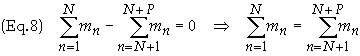
The right side of Eq. (8) is simply the expression for conservation of mass. Thus it is shown when the Lorentz transformation is applied to the 4-momentum and the conservation of 3-momentum is assumed to be valid in all inertial frames of reference then it follows that mass is a conserved quantity.

Back to Physics World
Back to Special Relativity