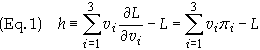
Force and Potential Energy in
Classical Mechanics
Back
to Physics World
Back to Classical Mechanics
The
energy function, h, for a single particle is defined in terms of the
Lagrangian, L = K - U where K is the kinetic energy of the
system and U is the generalized potential of the system which is a
function of the generalized coordinates and possibly a function of generalized
velocities and in general a function of time.
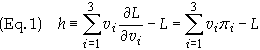
where
is the generalized
or canonical momentum. It can be shown
that
If h
is the total energy of a system then it can readily be shown
that
Where V
is the systems potential energy. Take the time derivative of Eq. (4) to obtain
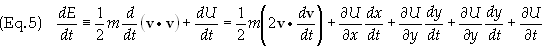
Eq. (5)
can be expressed as
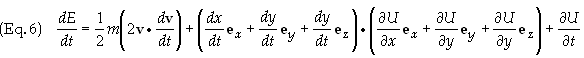
Eq. (6)
may be simplified as follows
If both U
is time independent then it follows from Eq. (7) that
Force
defined as the time rate of change of the particle’s momentum, i.e.
Substituting
F into Eq. (7) gives
This
will be true if either
is perpendicular to v or
. Therefore
Example:
Charged Particle in an EM Field
Consider
the Lagrangian for a charged particle moving in an electromagnetic field. The
Lagrangian is [1]
In the
present case the generalized potential has the value
Where V
= qF is the
electrostatic potential energy of the charged particle in the Coulomb field F.
U has the form of a velocity dependant potential and is not an
explicit function of time. The canonical momentum is found to be
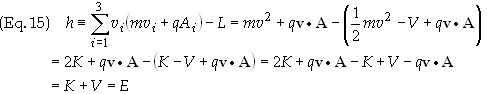
In this
case h is the total energy of the particle. Assume that V (thus F)
and A do not depend on time explicitly. Then L also does not
depend on time explicitly. Thus Eq. (10) will hold true. I.e.
It can
be shown by direct calculation using Lagrange’s equations that
Therefore
. On the other hand if B = 0 then
and we’d have
References:
[1] Classical
Electrodynamics – 3rd Ed., J.D. Jackson, John Wiley & Sons,
(1998), page 582 Eq. (12.9)