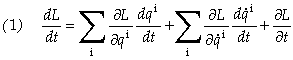
Relativistic Energy

For a relativistic particle the total time derivative of the Lagrangian, L = K - U, is given by

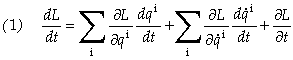
where and U is a function of position and velocity and time called the generalized potential. Considerations of such a potential is required in relativity since it produces velocity dependant forces and it is well known that all forces in relativity must, in general, be velocity dependant in an arbitrary frame of reference. However one can choose a particular frame to work in such that the force does not depend on velocity but only the general case will be considered here. Using Lagrange’s equations

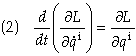
Eq. (1) can be written as

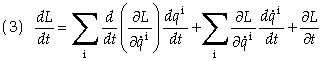
or

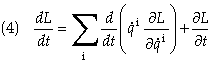
Rearranging terms we get

This can be written in terms of the energy function, h, defined as

Eq. (4) then becomes

If the Lagrangian, L, is not an explicit function of time then it follows that h = constant, i.e. h is an integral of motion. Substituting L into Eq. (6) gives

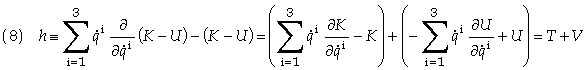
where

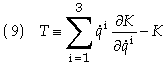
To evaluate this relation first find the partial derivative of K

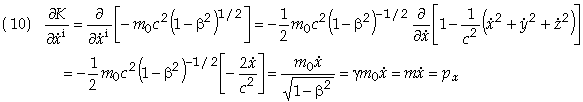
Similar expressions hold for the other components. We may now evaluate T to obtain

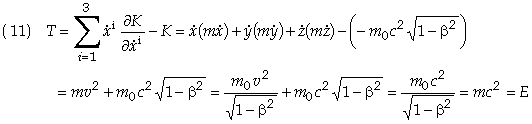
The second quantity on the right hand side of Eq. (8) is defined as

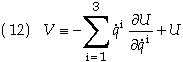
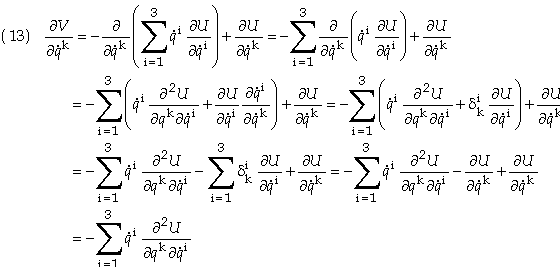
When U is linear in velocity terms then V will not be a function of the generalized velocities but will at most a function of position and time. V is then referred to as the potential energy of the particle [Ref 4]. In such cases h is the total energy, W, of the particle. I.e.

If the particle is moving in an electromagnetic field then the Lagrangian is given by

In this Lagrangian U is given by

Since U is a linear function of velocity then it follows that the potential energy is well defined and has the value defined by Eq. (12). First find the partial derivative of the generalized potential with respect to the velocity

Similar expressions hold for the other components. Eq. (12) now becomes

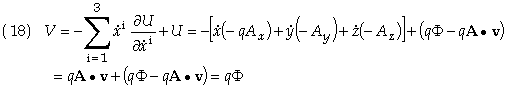
which is the expected result. The total energy of a particle in an EM field is therefore given by

[1] Classical Mechanics - 3rd Ed., Goldstein, Poole & Safko, Addison Wesley, (2002), page 61, Eq. (2.53)

[2] Ref. 1 page 313 Eq. (7.136)

[3] Classical Electrodynamics - 2nd Ed., J.D. Jackson, John Wiley & Sons, (1975), page 574 Eq. (12.9)

[4] The Variational Principles of Mechanics – 4th Ed., Lanczos, Dover Pub., (1970), page 33, Eq. (18.5)