Gravitational Red Shift

Back to Physics World
Back to General Relativity

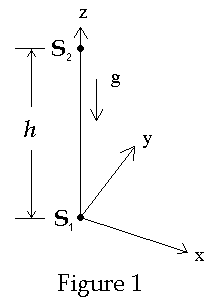
Gravitational red shift is often interpreted as the result of spacetime curvature. The argument used to arrive at this conclusion is based on that proposed by Schild [1]. From herein it will be assumed that the gravitational field is static, otherwise there is no guarantee that there will be a gravitational red shift in all generality. Marsh and Nissim-Sabat gave a counter argument to Schild in the American Journal of Physics, [2] which is discussed below. Schild’s argument is basically the following; consider two systems S₁ and S₂ located in a gravitational field as shown in Figure 1.

Let the gravitational potential F(z) be defined such that F(0) = 0. Two pulses of light are emitted from S₁ towards S₂ spaced in time by the amount Dt as reckoned by coordinate time which is the term will use to the time as measured by observers in S₁. Denote these events by E₁(first pulse emitted from S₁) and E₂ (second pulse emitted from S₁). Each pulse travels to S₂ where they are recorded by observers in S₂. Denote these events E’₁ (first pulse received at S₂) and E’₂ (second pulse received at S₂). The worldlines are drawn curved to allow for the possibility that the gravitational field may act on the light in an unknown way. In general light does not travel at a constant speed in a gravitational field but depends on the gravitational potential. A curved line represents a varying speed of light. The world lines of these light pulses are typically drawn in diagrams such as that shown in Figure 2 below.

    
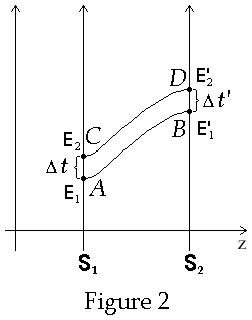
     Regardless of how the field acts on the light, the worldlines will be congruent. By this it is meant that the shape of the curves will be identical but merely translated upwards on the spacetime diagram. AC = BC as shown in Figure 2. However, it is argued, since it is known from experiment that Dt > Dt’. Thus, Schild argues, AC ¹ BC and therefore the diagram is non-Euclidean, curved, spacetime. That the first derivation of gravitational redshift by Albert Einstein was in flat spacetime never seemed to bother Schild!
     What’s wrong with Schild’s argument? First one needs to be careful when interpreting the statement "The frequency of light decreases..." Caution must be exercised when using "the" when discussing relativity. The frequency reckoned but which observer? Which clock is used to reckon this change? Secondly we note that when spacetime diagrams are drawn to illustrate Schild’s argument, they are always drawn without a scale on the time axes. This lack of a time scale leads one to make easily make an error. Each time axis represents the worldline of the clock located at the origin of its coordinate system. The clock in S₁ records the coordinate time in S₁ whereas the clock in S₂ records the coordinate time in S₂. Since the two axes represent the time on different clocks which run at different rates the scale of the t-axis does not have the same scale as the t’-axis. The correct diagrams are shown in Figure 3 below

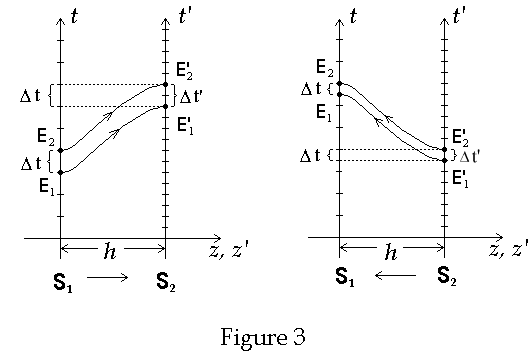
     Note that these are really two spacetime diagrams superimposed on top of each other, the difference between them being the origins are separated by the distance h, the spatial separation of the clock, i.e. S₂ is located at a distance h higher in the gravitational field than S₁.  Thus S₂ is located at a higher gravitational potential than S₂. In addition we add a scale to the times axes of both S₁ and S₂. Figure 3 shows a spacetime diagram of two light geodesics emitted from S₁ towards S₂. The t axis represents the worldline of clock C₁ located in S₁. The t’ axis represents the worldline of clock C₂ located in S₂. The proper time between two events on a particular clock is defined as the time recorded on a clock that passes through both events along a given worldline. The coordinate time of an event as recorded in S₁, is found by projecting the event on the t’ axis onto the t axis (shown by dotted lines in Figure 3). The time interval is defined as the difference between the times of the events as recorded in S₁. Let Dt be the proper time interval between events E₁ and E₂ as recorded in S₁ and Dt’ be the proper time between events E’₁and E’₂ as recorded in S₂. Then Dt is the proper time between E₁ and E₂ and Dt’ is the proper time reckoned by observers in S₁ between E’₁ and E’₂. From the spacetime diagram in Figure 3, Dt is also the coordinate time as measured by observers in S₁ between the events E’₁ and E’₂. However, due to the different time scales, while the emitter releases a pulse separate in time by one unit S₁ receives the pulses separated in time by two units. As seen in Figure 3 Dt’ > Dt. In the diagram Dt = “1 unit of time” and Dt’ = “2 units of time.” In the diagrams we assume that C₂ runs twice as fast as C1 and therefore Dt’ = 2Dt. This means that the frequency, at which the pulses leave S₁, as recorded on C₂, is twice the frequency at which the pulses arrive at S₂, as recorded on C2. However, as reckoned by observers in S₁ the rate of depart of the pulses from S₁ is the same as the same rate that S₂ receives them.

Schwarzschild Metric

In order to describe gravitational redshift consider a spherical symmetric massive body (e.g. planet, star, black hole etc.) whose gravitational field is described by the Schwarzschild metric

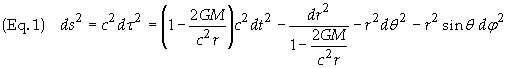
ds is a scalar quantity which represents the invariant spacetime interval between two events in spacetime. For two events which have a spacelike spacetime separation the proper time between two events is related to ds by ds = c²dt². t is known as the coordinate time. r is the Schwarzschild radius, defined so that the circumference of a sphere at radius r is 2pr. It's also known as the coordinate radius or reduced circumference. q and f represent the typical spherical angles in a spherical coordinate system. The coordinate time t is defined as the time recorded by a clock located far away from the gravitating body. This time t is thus referred to sometimes as far-away time. Such a clock will be referred to below as a coordinate clock.
     Consider two clocks C_e (Clock at emitter) and C_r (Clock at receiver) – which are of identical construction - located at the spatial coordinates P_e (r_e, q_e , f_e) and P_r (r_r , q_r , f_r ). We wish to analyze the frequency of the light, locally, at both P_e and P_r . To do this we consider a sequence of pulses, which leaves C_e, and then analyze the rate at which these pulses arrive according to observers reading the time on C_r. We adjust the rate of the pulses emitted to be the frequency of the emitted light. We then determine the rate at which the pulses arrive at C_r and we will then have found the frequency of light, which arrives at C_r.
     Let C_e emit two flashes of light, which then travel to C_r. Let each pulse of light travel along the same spatial path. Since the coordinate time t depends only on the spatial path the light takes, then the time it takes for each pulse to travel from C_e to C_r will be the same for each pulse.
     Define

Dt_e = Coordinate time interval between the two signals which are emitted from C_e

Dt_r = Coordinate time interval between the two signals which are received at C_r

It then follows that

Therefore the frequency of the light, as measured by any single observer, does not change as the light moves through the gravitational field!
    According to Eq. (1) for two closely spaced pulses dt_r = dt_e . Let dt = dt_r = dt_e = the coordinate time interval. The time interval recorded on C1 between the emission of two pulses is the proper time between the two pulses and will be denoted by dt_e . The time interval recorded on C2 between the reception of the same two pulses is the proper time between the two pulses arriving at C₂ and denoted dt_r.  These intervals are related to the proper time intervals through the metric. For simplicity let dr = dq = df = 0 (i.e. the clocks are at rest).  Substituting these into the Schwarzschild metric gives

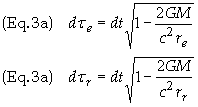
Upon rearranging terms we get

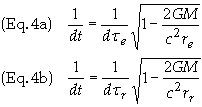
Note that frequencies are related to time intervals by f = 1/dt. Define the following frequencies

f = frequency as measured on far-away clock

f_e = frequency as measured on C_e

f_r = frequency as measured on C_r

Then

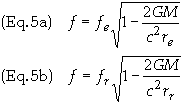
Equating Eq. 3b by Eq. 3a becomes upon rearranging terms

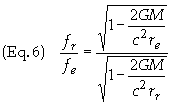
This is the relation for gravitational redshift. Eq. 5 shows that when r_e ¹ r_r then f_e ¹ f_r. Consider now that the light consists of photons. Multiply Eq. (4) through by Plank's constant h, noting that the energy of a photon is E = hf, to get

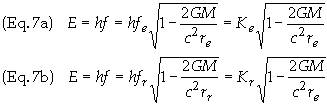
E is then the energy of photon as measured by a far-away observer. K_e and K_r are the energies of the photons when measured by devices collocated with the clocks at P_e and at P_r respectively. These energies may be thought of as the kinetic energies of the photons. Eq. 5 can be rearranged to give

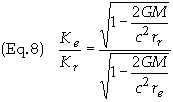
Eq. 6 can be simplified by using the approximation (1+d)ⁿ » 1 + nd,

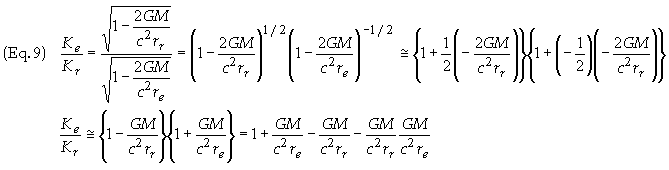
neglecting second order terms

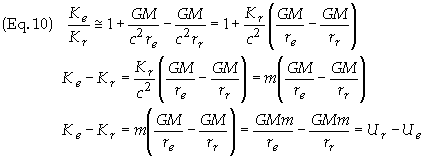
whew m = K_r /c² = gravitational mass of photon as measured by observer at r = re. U º -GMm/r = Gravitationnal Potential Energy of photon and K = Kinetic Energy of Photon (energy of photon measured locally). Then

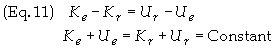
Define E = K + U = Kinetic Energy + Potential Energy = total inertial energy. Therefore

which is simply the expression for the conservation of energy. Since this holds for any r it follows that E = constant along the photon's trajectory. I.e. The total energy of a photon moving through a gravitational field is constant.

[1] A. Schild, Monist 40, 20 (1962) Evidence for Gravitational Theories, edited by C. Moller (Academic, New York, 1962); Conference Internationalesur les theories relativistes de la gravitation, edited by L. Infeld (Pergamon, Oxford. 1964).
[2] Does a gravitational red shift necessarily imply that spacetime is curved?, by G.E. Marsh and C. Nissim-Sabat. Am. J. Phys. Vol. 43, No. 3, March (1975)

Back to General Relativity
Back to Physics World