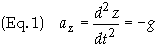
The Gravitational Field of a
Directed Beam of Light

Back to Physics World
Back to General Relativity

The energy density for an electromagnetic field is given by

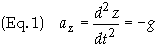
The electric and magnetic fields are related to the electric potential, F, and the magnetic vector potential, a, through Maxell's equations, which in differential form are given by

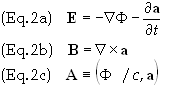
A is the 4-potential whose components A^a, is used to define the components, F^ab, of the Faraday tensor F. The stress-energy-momentum (SEM) tensor for the electromagnetic field, and the components of the Faraday tensor are defined, respectively, as

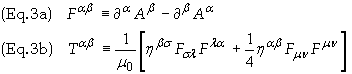
Using coordinates such that x^m =(ct, x, y, z), the Stress-Energy-Momentum (SEM) tensor, for radiation propagating in the +x direction, in Eq. (3b) becomes

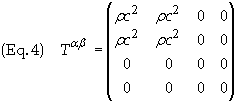
Let h_ab º diag (1, -1, -1, -1) = h^ab. Define the following quantities

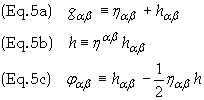
The linearized Einstein field equations are [4]

where T_ab = h_amh_bnT^mn, which, for a directed beam, is

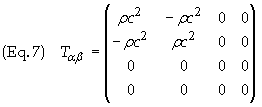
Assuming time independent matter distributions (no retardation effects are present) the solution to Eq. 11 is [2]

 Substituting the values T₀₀ = rc², T₀₁ = -rc², T₁₁ = rc², for the SEM tensor we get

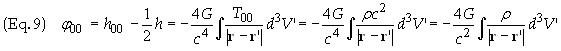
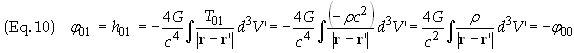
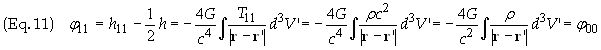
 f₁₂ = f₁₃ = f₂₂ = f₂₃ = 0. Applying these values to the definition of f_ab, i.e. Eq. (5a), give

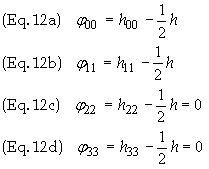
h₂₂+ h₃₃+ h = 0     =>     h₂₂+ h₃₃ = -h =0

Evaluate h by substituting the values above

h º h^abh_ab = h₀₀ – h₁₁ - h₂₂ - h₃₃ = h₀₀ – h₁₁ – (h₂₂ +h₃₃) =  h₀₀ – h₁₁ + h = 0

which implies h₀₀ = h₁₁. This and the relations above yield the solution

h₀₀= f₀₀, h₀₁ = -f₀₀, h₀₂ = h₁₂ = h₁₃ = h₂₃ = h₂₂ = h₃₃ = 0

The metric may therefore be represented solely in terms or h₀₀= f₀₀

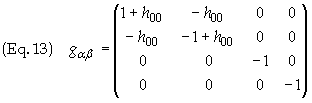
For a thin beam of radiation along the z-axis with a linear mass density r the value f00 is then found to be (r² º x^{2 +} y²)

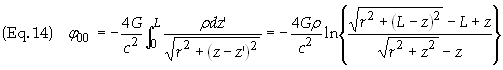
Motion of Light Ray:  In order to arrive at an expression for the velocity of a light ray in this gravitational field, defined by the metric in Eq. 18, first write out the corresponding expression for the spacetime interval

Since a light rays move on null geodesics set ds²= 0. After dividing through by cdt Eq. 20 becomes

where b_x º v_x /c etc. Let initial velocity of the test ray be in the direction parallel to the x-axis.   Then, initially, b_y = b_z = 0. With these values Eq. 22 has two solutions

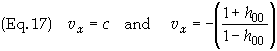
Since we started with the assumption h₀₀ << 1 the quantity in the brackets in the second equation is positive and therefore v_x is negative.  Therefore a test light ray moving in the +x direction, the same direction as the flow of radiation has the same speed regardless of where in the field the ray is located. If the ray is moving in the opposite direction the speed of light depends on the spatial coordinates as is usual for motion if a gravitational field.

References:

[1] On The Gravitational Field Produced by Light, Tolman, Ehrenfest and Podolsky, Physical Review, Vol. (37), March 1, 1931, pg 602-615.
[2] Relativity, Thermodynamics and Cosmology, Richard C. Tolman, Dover Pub, Sections 112-115 cover more aspects of the gravitational field generated by light than is presented here.
[3] Relativity; Special, General and Cosmological, Wolfgang Rindler, Oxford University Press, pg. 322, Eq. 15.28
[4] Ref. 3, pg. 321, Eq. 15.27

Back to General Relativity
Back to Physics World