Gravitational Field in a Cavity
Back
to Physics World
Back
to General Relativity
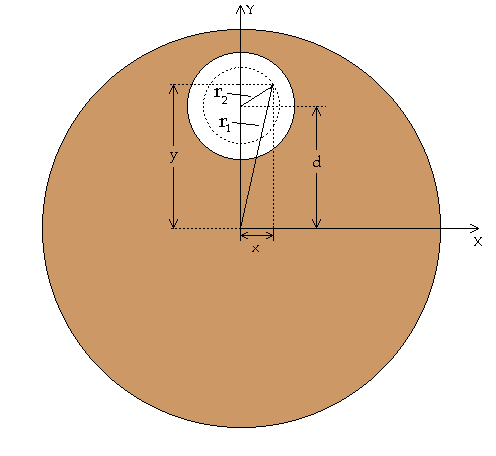
Consider a sphere of
uniform mass density r shown below

It is well known that the
gravitational acceleration field
g1=
g(r1)
within
the sphere is given by
![]()
The field is determined at
the displacement r1 measured
from the center of the sphere. Consider now a spherical region contained
entirely within the sphere above. Let the displacement of the center of this
region from the center of the sphere be d. The gravitational field g2
= g(r2)
due just to this region is
![]()
where the field is
determined within the region at the displacement r2 measured
from the center of the region. That is r1
= r2 + d
(note d = R j = constant).
Note:
r1
and r2
have different origins.
Next let the spherical
region be subtracted from the sphere to form a cavity. The resulting
gravitational field g at any point within the cavity at the
displacement r1
is
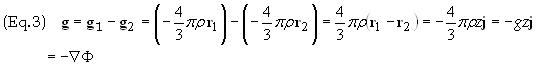
where F = gz + constant, g = (4/3)pGrR.
This same result could
have been obtained by integration of over the source, i.e. sphere with uniform
mass density r with a cavity. In situations when the sources of gravity are
static and the gravitational field weak enough such that objects cannot
accelerate to relativistic velocities the gravitational field may be
approximated to a high degree of accuracy using the so-called weak field
limit. In this case the gravitational field in a cavity will be highly
uniform. However the situation is more complicated since spherical cavity
will not have a well-defined meaning. It can be shown [1] that
in this approximation the integral for the Newtonian potential is the same as it
is in Newtonian gravity, where the mass density r
is now the rest mass density. The variables of integration are more akin to
"addresses" rather than to "distances" as they were in
Newtonian gravity. These "addresses" serve to label the spatial
co-ordinates of the sources. The Newtonian potential in the weak field limit
will still be F
= gz + constant. Such a distribution of mass is finite and thus represents a
realistic source in general relativity for a uniform gravitational field to a
high degree of accuracy.
References
[1] Gravitation, Charles. W. Misner, Kip S. Thorne, John Archibald Wheeler, (1973), sect 6.6.