![]() Reasons for the "New Theory..." creation
Reasons for the "New Theory..." creation
We began realization of works in the sphere of dynamics of rotors hanging in a vertical position in 1970. Our works have been successfully completed by creation of several centrifugal stands and a number of autobalancing devices patented abroad and in the USA as well.
First of all we were interested in unbalanced rotor physics processes. One of our successes was the new correct understanding of disk rotor with dynamic unbalance features.
We have developed the liquid autobalancing devices operation theory, which in a consequence was modified for balancing machine operations calculations with disbalance pulse removal.
Besides, the criterions of automatic balancing and application methods for evaluation of serviceability and creation of new autobalancing devices were developed.
 |
Yury Zhyvotov reports to President of USSR AS Mr. A.P.Aleksandrov, member of USSR AS Mr.V.F.Utkin, Corresponding Member of Ukrainian AS Mr. A.Y.Smetanin on discovered features of disk-type rotor dynamics and balancing possibility by self-alignment devices patented in French, USA, Germany, and Japan |
The part of our researches was published in the Academy of Sciences, former USSR journals, in particularly in the journals:
"Machinebuilding", M: , Science, 1988, No.1, page 12-20;
"Machinebuilding ", M: , Science, 1989, No.2, page 71-77.
These journals were reissued abroad in English.
But we could not use theoretical investigations in the sphere of dynamics of rotors in the process of realization of our works. A system of differential equations is a basis of those investigations. The equations are obtained bi way of differentiation of potential and kinetic power of the rotor.
We also noticed that methods based on usage of trial freight and graph analytical calculations of disbalances, are used of the theory and practice of balancing in spite of success in the sphere of dynamics of rotors. We did not find acceptable explanation of a phenomenon of rotor's self-centering either. And the system of differential equations describing rotation of the rotor under the influence of static and moment unbalance (when eccentricity is 0) was the most doubtful.
In addition, we have come to a conclusion that the fundamental theory is discrepant and considerably differs from practice in spite of intensive development of rotor dynamics in elastic bearings during a century.
We closely studied the existing literature on rotor dynamics and searched for the answers to questions:
1. Under what forces the center of rotor weights directs to rotation axis at unlimited increase of speed?
2. What reasons result in Sommerfeld effect ?
3. For what purposes the nature has provided the phenomenon of resonance?
4. On what basis the theory of oscillations is transferred on rotors rotation?
5. Why it is considered that for obtaining equations of unbalanced rotor dynamics it is enough to add disturbance forces in a right member of equations of own oscillations of ideally balanced rotor?
6. Why having available aerodynamic forces the rotor rotates with speed of the shaft?
7. For what reason should we use differential equations, if at this the linearization of used values is made?
8. Could Lagrange method result in obtaining false equations?
9. Why in balance engineering the main methods of balance identification is carried out with the help of trial plummets?
Searching answers to these issues A. Zhivotov has proposed and formulated a new hypothesis about nature and physics of rotation process of unbalanced rotor. This hypothesis has given the answer to all set above issues.
Problems in Classical Mechanics
The studies have been accomplished in period of 2000 through 2005 revealed serious weaknesses in the presenting the basics of classical mechanics.
1. Is a Material Point the Unsuccessful Model of a Body?
Existing scientific and educational literature presents basics of mechanics using such a concept as "material point". A material point represents a model of a body. Moreover, such a model does not take into account real body's moments of inertia. As a result of this, existing engineering mechanics, in fact, studies only rectilinear motion of a body under effect of forces being applied to its center of gravity. Such mechanics are not in compliance with present-day requirements. A transfer from such a body model as a material point to the model being represented as a physical point has resulted in creation of a new theory: the theory of rotated bodies.
As a consequence, a necessity of radical reviewing of certain chapters of classical physics and engineering mechanics course manuals has occurred. In particular, the following theories require revisions: the gyroscope theory, the theory of body's rotation about fixed point, the theory of body's rotation, one-support body rotation, and kinematics.
2. Vector Definition. Is it Strict Enough?
The vector calculus was widely taken up in classical physics and engineering mechanics. All fundamental equations are written in a vector form or deducted using the rules of vector operations.
Getting into the style of using vector calculus has resulted in application of pseudo vectors in mechanics, garbling of body motion physics, especially for what concerns a curvilinear motion.
A notion of the vector in mechanics turned-out to be so expanded that many specialists are ready recognize an ordinary weather vane as a vector value. An existing definition of the vector allows making such an assumption. Some authors of educational manuals became aware of a problem caused by erroneous definition of the vector. They point-out that there are some values having both modulus and direction but being not vectors.
It is obvious that in terms of the strict science the situation cannot be treated as normal.
3. Is the Radius-Vector the Vector Value?
The radius vector plays a specific role in mechanics.
It is considered as a vector value. Belonging of a radius-vector to the vectors is proved basing on concepts of the body's displacement vector, velocity vector, or acceleration vector. Suffice it to draw an attention to the fact that examples of the vectors being cited in literature (such as velocity vector, acceleration vector or force vector) characterize a body's spatial motion regardless a coordinate system. The fact that the vector values characterize body's motion is fully ignored for unknown reasons. The same for ignoring the fact of independency of vector value on a coordinate system.
Referring to universally recognized vectors, the vector concept is formulated as a value having both modulus and direction. If it is considered that vectors should characterize the spatial motion of a body, then it becomes obvious that a radius vector is not a vector value. Firstly, a radius vector characterizes a body's position in a selected coordinate system. Secondly, a coordinate system is a human invention intended for studying spatial motion of bodies and, therefore, does not exist in reality. So, a radius-vector is just an ordinary coordinate of the body's location in selected coordinate system not being a vector value.
4. Does a Displacement Vector Have Any Explanation?
A body's displacement vector is defined as a difference between two radius-vectors determining the body's location in the coordinate system after a lapse of certain time.
The subject of an incident with a displacement vector is that its voluntary interpretation provides a basis for considering a direction of the displacement vector as being opposite to the velocity vector. To make sure of that, it is necessary to analyze a ball fall-down on the floor while dropping it from a certain altitude assumed to be a pole serving as an origin of the radius-vectors. Let us select the radius vector characterizing the ball position with respect to the pole at the beginning, and the radius vector describing the boll position upon bounce off the floor. Performing the vector subtraction of two radius-vectors we can obtain a result indicating that the displacement vector is directed against the velocity of bounced ball.
By the way, such a fallacy is utilized in engineering mechanics while deriving the fundamental equation of the oscillation theory.
5. Do the Inertial Forces Represent Virtual Forces? Is the Centrifugal Force a Virtual Force?
One of the classical physics and engineering mechanics dogmata is an assumption that an inertial reference system is free of inertia forces. Such a statement is migrating from one educational manual to another one in spite of the obvious effect of inertia forces when attempting to slow-down the body's motion or when moving alone a curvilinear trajectory. This statement exists despite the fact that a car turnover at a deep-lunged torque occurs in an inertial reference system under effect of a centrifugal force.
In that case it is forgotten that the first law of Newton is also referred to as the law of inertia.
It is also forgotten that Newton's doctrine is built on the basis of inertia laws and forces whereby bodies are interacting when in collision are the inertia forces.
6. Is the Centripetal Force a Real Force?
The classical mechanics has expelled the inertia forces originating when a body is moving along a forced curvilinear trajectory and introduced centripetal forces. The planetary motion around the Sun became a reason for that. Really, the motion of the planets around the Sun is performed under effect of the natural force of the Sun gravitation, which has been considered by Newton as a centripetal force. Copying a planetary motion mechanism, the classical mechanics state that rotation of a small ball tethered to the center of rotation is also performed under an effect of centripetal forces in the absence of inertia forces.
The problem of tethered small ball rotation lies in the fact that the classical mechanics are not able to find out a natural force in the center of rotation forcing a small ball to perform its circular rotation. As a way-out from such situation, the classical mechanics introduce an understanding of reaction forces as centripetal forces affecting a small ball and being originated at the fixed center of rotation. Dubiousness of such conjecture is obvious because reaction forces are originated as a response to the action of real forces being applied to the body. But in case of a tethered small ball rotation, the classical mechanics do not recognize an existence of such a real force.
7. Coriolis Force
It is often said about the Coriolis force - a mysterious force. A conclusion about existence of the Coriolis force has been made while comparing the motion of a material point in inertial and non-inertial reference systems. The mathematicians have calculated an equation term that is originated when transferring from an inertial reference system to a non-inertial one. In fact the Coriolis force did not obtain any physical substantiation.
However the influence of that force on some physical natural processes was so sufficient that the missing term of the equation has been recognized by the whole world as a force. True, the Coriolis force is also considered as an imaginary force. Such an imaginary force is eroding river banks, change directions of air streams. What a strange stand has been taken by the classical mechanics! In the reality, the Coriolis force is a simple inertia force, which really exists in an inertial reference system.
8. Is the Rotating Coordinate System an Inertial Reference System?
A yearning for refusal of inertia forces from inertial reference systems has compelled the coryphaei to acknowledge inertia forces in rotating coordinate system. Therefore, a rotating coordinate system is generally agreed of being considered as an inertial reference system. Presence of centripetal forces during the rotational motion is an essential proof. This is a quite dubious substantiation. As it was already shown above, the classical mechanics do not explain a cause of origination of centripetal forces: the reaction forces.
Moreover, there are two mutually exclusive statements indicated in the educational literature. The first one says that a centripetal force is originated when a small tethered ball is rotated. The second statement says that the circularization of a small tethered ball proceeds under an effect of centripetal force.
9. Newton and Mechanics
Analysis of the rotation of a small ball tethered with a fixed center is traced to Newton. In reality, Newton studied rotation of two small balls joined by means of a mechanical link: a thread. In that case, the analysis of small balls rotation was based on their natural attempt of keeping on rectilinear inertial motion. It is obvious that Newton intentionally considered a simultaneous rotation of two small tethered balls. This fact witnesses: Newton understood that there is no gravitational or natural centripetal forces in the rotation center. So it is confirmed that modern mechanics require corrections also in terms of historical provisions.
10. Inertial Mechanics
In these shorn notes some problems of classical physics and engineering mechanics have been touched. There are much more problems in modern engineering mechanics. Here we have touched only those problems that found their new solutions in a number of scientific papers. The papers set forth the basics of the inertial mechanics. They give grounds for reviewing the basics of Lagrangian mechanics and return to the original positions of Newton's doctrine have been undeservedly forgotten.
LIST OF THE SCIENTIFIC PAPERS PUBLISHED
By Mr. Zhivotov Alexandr Y.,
Leading Engineer of Yuzhnoye State Design Office named after M. K. Yangel: www.yuzhnoye.com
(Over a period from 2000 to 2004)
1. N. M. Belyaev, A. Y. Zhivotov. Centrifuge with a continuously working liquid balancing device to test the units and assemblies for rocket-space equipment // Bulletin of Engineering Sciences Academy of Ukraine. Special issue of Heavy and Transport Engineering Industry Department. - 1997. - p. 45 - 49. Printing Office of AO Dneprotyazhmash, Dniepropetrovsk.
2. N. M. Belyaev, A. Y. Zhivotov. On the point of liquid self-balancing device engineering // Pridnieprovsk Science Bulletin. Engineering Sciences. - 1998. - ? 55 (122). - p. 45 - 48. Science and Education Publishing House, Dniepropetrovsk.
3. N. M. Belyaev, A. Y. Zhivotov. Parameters of the liquid balancing device // System Engineering and Characteristic Analysis of Aerospace Equipment. Collected Scientific Papers - 1998. - Volume 1. - p. 124 - 129. Educational Book Publishing House, Dniepropetrovsk.
4. A. Y. Zhivotov. Application of the balancing device during bench tests of the rocket-space equipment // Engineering Sciences: Problems of Theory and Practice. Inter-college Collection of Scientific Papers. 1999. - Issue 1. - p. 53 - 61. Science and Education Publishing House, Dniepropetrovsk.
5. A. Y. Zhivotov. Computation of the balancing device intended to develop an aircraft engines // Dniepropetrovsk University Bulletin. Rocket-Space Engineering. -2000 - Issue 4. - p. 56-64. DNU Printing Office, Dniepropetrovsk.
6. A. Y. Zhivotov. Features of dynamics of the rotor with moment unbalance // Instrument-making Technology- 2000. - ? 1. - p.12 - 17. NITIP Publishing House, Kharkhov.
7. A. Y. Zhivotov. Rotation features of the disc rotor with static unbalance // Eastern-Ukrainian National University Bulletin. - 2001. - ? 2 (36). - p. 218 - 225. SNU Publishing House, Lugansk.
8. A. Y. Zhivotov. Rotation features of the disc rotor with dynamic unbalance // Eastern-Ukrainian National University Bulletin. - 2001. - ? 11 (45). - p. 116 - 125. SNU Publishing House, Lugansk.
9. V. V. Akimenko, A. Y. Zhivotov, Y. V. Brazaluk. Simulation of rotation of a vertical suspended rotor with static unbalance // Eastern-Ukrainian National University Bulletin. - 2001. - ? 7 (41). -part 2. - p. 19 - 25. SNU Publishing House, Lugansk.
10. A. Y. Zhivotov. Liquid balancing device for static balance at constant finite fluid flow, balancing accuracy // Space Science and technology. - Supplement to the magazine. - 2001. - V. 7, ? 1. - p. 33 - 37. NKAU Publishing House, NASU (National Academy of Science of Ukraine), Kiev.
11. A. Y. Zhivotov. Identification of rotating cylindrical rotor unbalances // System Engineering and Characteristic Analysis of Aerospace Equipment. Collected Scientific Papers - 2001. - V.خ - p. 82 - 90. Educational Book Publishing House, Dniepropetrovsk.
12. A. Y. Zhivotov. Rotation features of wheel set axles with dynamic unbalance // Transport: Collected Scientific Papers of Dniepropetrovsk State Technical Railway Transport University. - 2001. - Issue. 8. - p. 42-51. New Ideology Publishing House, Dniepropetrovsk.
13. A. Y. Zhivotov. Unbalance identification for disc rotors of mining equipment // Geotechnical Mechanics: Interdepartmental Scientific Papers Collection. - 2001. - Issue 25. - p. 127 - 132. Publishing House of Geotechnical Mechanics of National Academy of Science of Ukraine, Dniepropetrovsk.
14. A. Y. Zhivotov. Rotation dynamics of the unbalanced rotors with pivoting and elastic bearings for mine ventilation installation // Geotechnical Mechanics: Interdepartmental Scientific Papers Collection. - 2001. - Issue 26. - p. 125 - 130. Publishing House of Geotechnical Mechanics of National Academy of Science of Ukraine, Dniepropetrovsk.
15. A. Y. Zhivotov. Dynamics of the disc rotor static unbalance taking into account bearing added mass // System Technologies: Mathematical problems of technical mechanics. Regional Inter-college Scientific Papers Collection. - 2002. - Issue 4 (21). - p. 24 - 27. System Technologies Publishing House, Dniepropetrovsk.
16. A. Y. Zhivotov. Dynamics of unbalance rotor with bearings having nonlinear characteristics // System Technologies: Mathematical problems of technical mechanics. Regional Inter-college Scientific Papers Collection. - 2002. - Issue 5 (22). - p. 35 - 39. System Technologies Publishing House, Dniepropetrovsk.
17. A. Y. Zhivotov, Y. G. Zhivotov. Dynamics of umbrella-type rotor with elastic bearing // Instrument-making Technology. - 2002. - ? 2. - p. 15 - 19. NITIP Publishing House, Kharkhov.
18. A. Y. Zhivotov. Rotation features for rigid rotor fixed on elastic bearings with dynamic unbalance // Space Science and technology. - Supplement to the magazine. - 2002. - V. 8, ? 1. - p. 58 - 63. NKAU Publishing House, NASU (National Academy of Science of Ukraine), Kiev.
19. A. Y. Zhivotov. Dynamics of the disc rotor with static unbalance taking into account aerodynamic drag influence // Instrument-making Technology. - 2002. - ? 1. - p. 46 - 50. NITIP Publishing House, Kharkhov.
20. A. Y. Zhivotov. Critical speeds of the two-bearing rotor with static and moment unbalance // Transport: Collected Scientific Papers of Dniepropetrovsk State Technical Railway Transport University. - Issue 12. - 2002. - p. 75 - 78. Publishing House of Dniepropetrovsk State Technical Railway Transport University, Dniepropetrovsk.
21. A. Y. Zhivotov. Rotation dynamics of statically unbalanced umbrella-type rotor with pivoting and elastic bearings // Zhitomir Engineering-Technological Institute Bulltine. - 2002. - ? 1 (20). - p. 3 - 7. Publishing Office of Zhitomir Engineering-Technological Institute, Zhitomir.
22. A. Y. Zhivotov. Dynamics of unbalanced rotor on the bearings with nonlinear characteristics // Technical Mechanics. Technical Mechanics Institute of NASU (National Academy of Sciences of Ukraine) and NSAU (National Space Agency of Ukraine). - 2002. - ? 1. - p. 76 - 81. Publishing House of Technical Mechanics Institute of NASU and NSAU, Dniepropetrovsk.
23. Zhivotov A. Y. New theory of rotor dynamics: dick rotor dynamics with static unbalance // IFToMM Sixth International Conference on Rotor Dynamics. - Sidney, Australia. - Proceedings - Volume 1. - 2002. - p. 1057.
24. Y. G. Zhivotov, A. Y. Zhivotov. Inertial features of the rotor rotation // Technical Mechanics. Technical Mechanics Institute of NASU (National Academy of Sciences of Ukraine) and NSAU (National Space Agency of Ukraine). - 2003. - ? 1. - p. 107 - 117. Publishing House of Technical Mechanics Institute of NASU and NSAU, Dniepropetrovsk.
25. A. Yu. Zhivotov, Yu. G. Zhivotov, Yu. V. Brazaluk. New theory of rotor dynamics: dynamics of umbrella - type rotor with flexible support // The 2nd international symposium on stability control of rotating machinery. ISCORMA - 2. - Gdansk, Poland. - 2003. - p. 331 - 340.
![]() Review "oscillatory" theory of rotor dynamics
Review "oscillatory" theory of rotor dynamics
1. Basic initial equation of the rotor dynamics under "vibration" theory is:
|
(1) |
Mr. Y. Kozheshnik believes it fail. He think two forces taken into account by the equation (1) form no closed triangle of forces (see Figure 1).
 |
|
| Figure 1 | Figure 2 |
It is clear that other scientists agree with falsity of the equation (1). These scientists now apply the following equation in their studies:
|
(2) |
Left part of the equation (2) is a part of free vibration equation of a system with one degree of freedom. Right part of the equation is a force cycling on the plane perpendicular to the system vibration axis. But equation (2) like equation (1) consists of two forces that form no closed triangle also.
Meaning of ![]() force
cycling is not clear, if other force does not cycle because the system has only one degree of
freedom.
force
cycling is not clear, if other force does not cycle because the system has only one degree of
freedom.
Additionally, note that any theory omits description of the same process by two different equations ((1) and (2)).
2. To correct the equation (1), it was made an attempt to insert the aerodynamic drag forces. The third force allowed closing the triangle of forces.
|
(3) |
Consequently, the equation (4) appeared.
|
(4) |
It is clear that new equations (3) and (4) are fallacious, if we take into account that the triangle of forces are "coupled" with a fixed point. Due to this the triangle of forces and, therefore, rotor should rotate about this point with a constant acceleration for unlimited time (see fig. 2).
3. Note also, that equation (3) only enabled getting dependence to determine an angle of the rotor turn about geometrical axis.
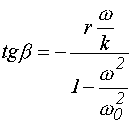 |
(5) |
However, assume that the rotor rotates under vacuum conditions (r = 0), so the dependence (5) "self-destructs". At the same time, the rotor rotation process under vacuum conditions is analogous to the rotor rotation subjected to the aerodynamic drag forces.
4. Existing "vibration" theory is low-informative. So equation (3) provides availability of a critical speed, allows getting dependence to evaluate this speed, determining a distance between rotation axis and center of mass and the rotor turn angle. In addition, it denotes a possibility of the rotor self-alignment. This is a limit of the "vibration" theory comprehension. (Accuracy of this information has not been considered in this case.)
5. Existing "vibration" theory collected data on the rotor dynamics features, but is unable to explain these effects and indicate ranges of effects.
These effects include resonance effect; Sommerfeld effect; self-vibration effect; effect of direct precession about shaft.
Therefore, based on equation (1), we can deduce that the rotor at unlimited acceleration self-aligns. However, it is impossible to explain why it occurs.
Accumulated data on the rotor rotation features is insufficient. So, It does
not reflect the rotor retrograde precession at changing of the turn angle from 90![]() to 180
to 180![]() . A fact that there is no a way
to stabilize the rotor position within angle range of 90
. A fact that there is no a way
to stabilize the rotor position within angle range of 90![]() to 180
to 180![]() had not been founded.
had not been founded.
6. The solutions of equations of "vibration" theory could not be applied to identify an unbalances, although the rotor unbalance identification is an inverse problem of dynamics. Due to this, the "vibration" theory is actually unusable in the theory of rotor balancing. The theory of rotor balancing emphasizes comparative analysis of the tests rotor launches with test loads.
7. General issue of the "vibration" theory is a statement that the rotor shaft performs bending vibrations (like planes of turning folk and spring beam). Actually, the shaft bends and rotates about the rotation axis in deflected position.
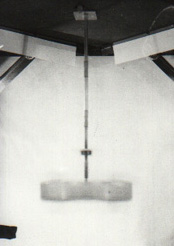 |
There is a process of balancing to use of the liquid automatic device for balancing a rotor |
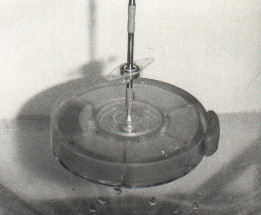 |
Before balancing, after balancing on supercritical speeds the rotor rotates by the "easy" party outside.
Pay attention! The liquid is going only in one tank. At vibration of a rotor the liquid serially would get in opposite tanks.
This evident example confirms, that the basic movement of a rotor is not vibration! |
8. Another important issue of the "vibration" theory is assumption that the rotor on the flexible shaft has one degree of freedom. In real environment, the rotor not only deflects from the rotation axis, but also has a possibility to rotate about geometrical axis. Evidently, that the rotor on shaft has two degrees of freedom.
9. According to the "vibration" theory, the torque is consumed to overcome the aerodynamic drag only. It is assumed that under vacuum conditions the torque equals zero if the rotor rotates with a constant speed. Nevertheless, it contradicts well-known Sommerfeld effect. We can adduce other evidence of equations (1-5) falsity, but provided proofs are sufficient.
April 08, 2009.
Quantity of visitings of a site.--------------------------------------------------------------- 26600
The messages in support of the "Vibration" theory of dynamics of rotors.--------- 0
So, the "Vibration" theory of rotor dynamics is erroneous!
What do you think regarding this?
![]() About the New Theory of Rotor Dynamics
About the New Theory of Rotor Dynamics
Dear colleagues! We inform you, that reviewers IFToMM 2003 have not found lacks of the inertial theory of a rotor dynamics and therefore have decided to not invite us to the congress and to not acquaint you with the new theory. Solution IFToMM 2003 exempts us from our ethical obligations to not publish papers prior to the beginning of work of the Congress. Therefore, we have made the Solution to publish both scientific papers on the Site
(http://www.geocities.com/newrotor)
The best regards,
Yuriy Zhivotov
(http://www.vibinst.org/default.htm)
From: Arne
Dear Yuriy, from the treatment that you get from well known scientists, I get the impression that this issue must be of the same dignity as the issue of the earth being flat or round. I think we see a sign of plain fear. I wish I was smart enough to fully grasp your traditional theory attack. What I miss as a simple student is an explaination in words on the level of simple language. Whenever or wherever available I would be most grateful to know. Regards Arne
From: Sasaki
I don't think I can understand the "new" theory, but reminded
me of these papers.
http://www.aa.washington.edu/faculty/eberhardt/Lift_AAPT.pdf
http://www.aa.washington.edu/faculty/eberhardt/lift.pdf.
Whatever the teory might be, the airplane flys! One theory explains one limited area of phenomenon. I hope the new theory would help realize an automatic self balancing mechanism of a centrifugal separator. Regards,
From: Ron Hartlen
I would agree with Arne. Can you tell us: 1) Are you saying the established
theory is wrong and yours is right? 2) Or, are you saying that your theory
is more complete and precise? 3) If so, what physical effect is involved
in the differences? 4) What is the practical significance? ie what is
the most important practical application? What mistakes could be made
by the classical approach, what might be overlooked, and what would be
the consequences for the machine design / analysis? 5) Or, is your work
mainly of "academic" interest? ps comments: a)sometimes the
academic community will continue dotting i's and crossing t's for fifty
years after a practical problem has been solved and the engineers have
moved on to do many other things. b) if you have something really new
and important, allow about thirty to fifty years for the establishment
to be persuaded
From: Yuriy
Zhivotov
Dear Arne, Sasaki and Ron Hartlen! We know about existence of three theories
of a rotor dynamics on the basis of the equations of a science about drag
of materials, the equations of progress of a body on a circumference (two
various methods) and the equations of the theory of oscillations.
The theory of a rotor dynamics, which is based on the equation of vibration of a body with one degree of freedom, counts the modern theory. This equation describes oscillations of a load, which is suspended on a spring. We have not found in textbooks how this equation for the description of a rotor rotation is received. Thus all three theories peacefully get on among themselves. The similar case is possible, if all three theories are defective or wrong.
I count, that the system a load - spring cannot be model of a rotating rotor and consequently the vibrating theory of a rotor dynamics is erroneous on understanding of physics of rotation of a body. A.Zhivotov has offered the inertial theory of a rotor dynamics (the fourth theory of a rotor dynamics) on the basis of model of rotating system of a rotor - supports with variable inertia moments. It is qualitatively new understanding of physics of rotation of body.
Therefore the inertial theory the nearest year or two will replace the vibrating theory in training programs or at carrying out of new researches if our papers will be published. It seems to me also, that engineers will operate also the new theory for designing machines as the inertial theory explains why there is this or that phenomenon.
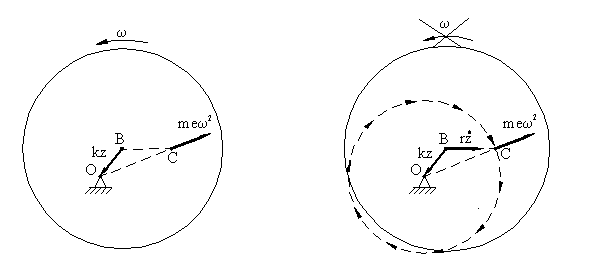
I think, that the inertial theory will undertake the responsibility for a prediction of results of experiments. I do not think, that all problems of a rotor dynamics are solved by a trial and error method, and all results of experiments are processed on a computer with the help of numerical methods. Pay attention, the existing vibrating theory does not explain dear Sasaki as the device for automatic balancing a rotor works or why there is a self-centering of a rotor of a separator. I am the author about 100 inventions. About 30 inventions (some inventions are patented in the USA) concern to automatic balancing devices. I had problems with an existing rotor dynamics same, as at dear Sasaki. The inertial theory explains why and as the turn of a rotor on 180 degrees occurs. In our paper figure is resulted. Allocate with a fat line a circumference.
Prolong line BC before crossing with a circumference and make a blot in this point. The blot represents a load, which creates an unbalance of a rotor. Place on a circumference a ball. If the rotor rotates, the ball will be will leave from the center of rotation (point O) on the greatest possible distance (line OB). You will see, that on subcritical speeds the ball increases an unbalance of a rotor as the ball settles down on one side with a blot.
However on supercritical speeds point O settles down between a point C and point B. The ball will leave also from the center of rotation (point O) and will take a place opposite to a blot. Thus, the ball balances a rotor. Our figure has helped you? The best regards, Yuriy Zhivotov
From: Sasaki
Dear a-zhivotov, Will you give us the US patent number? I will check it!
Regards,
From: Yuriy Zhivotov
Dear Sasaki! These inventions concern to 1973-77. At that time we have
denied idea about a scope of automatic balancing a disk rotor with the
help of two automatic balancing devices which are established in two planes
of a rotor on both sides from a center of masses. Five inventions have
been selected for patenting in France, Germany, Japan and USA. By existing
rules of patenting in Germany and in France these inventions are published
completely. We have received on them positive Solutions. USA has given
out two patents. However I cannot find them in archive. NNN 561099, 772362,
775645, 784482, 786488, 796674, 836539, 836540, 836541, 847102, 864946,
869447, 899447, 939984, 949366, 949367, 949368, 949369, 949370, 968642,
970157, 997314, 1002863, 1002864, 1004789, 1012061, 1015272, 1105767.
Class G01M 1/38 The best regards Yuriy Zhivotov
From: Sasaki
There seems no proof of patent in any country.
From: Yuriy Zhivotov
Dear Sasaki! Only for you we make exception and we prove, that we really
have patents the USA. We also give example publications of our invention
in Germany. Other four inventions also are published in the countries
of patenting of inventions, which we have mentioned in the previous letter.
However do not ask us that we searched for these publications.
Patents the USA N 4295386, N 4295387.
We have paid attention that you participated in discussion of a theme "Lomikin Effect". We have read paper about which you have mentioned. We have understood, that the effect arises, if in the pump to fill a liquid. It is a condition at which there is an effect. However we have not found explanations why this effect arises. The author of paper will mention, that hydrodynamical force of stabilization provides effect. What is this force? It seems to me, that if to us will give the equation of this force, we shall give theoretical dependence (not empirical) for specifying critical speed. We hope, that the inertial theory of a rotor dynamics http://www.geocities.com/newrotor allows explaining effect. However we doubt, that the equation for specifying this force will exist. It is a pity, that we today cannot receive the similar equation independently. The best regards Yuriy Zhivotov
From: Sasaki
Dr. Yuriy Zhivotov, Thank you for the US patent numbers. Perhaps you are already aware of this product, or would be intereted in, externally pressurized bearing. http://bpb-co.com/bpb/Home.htm Best regards,
From: Yu. Zhivotov
Dear Ron Hartlen! If you have visited our Site you could find out, that
in the critical review of the vibrating theory of a rotor dynamics we
refer to opinions and conclusions of authoritative scientists, which created
and have evolved the theory. Thus, authoritative scientists have recognized
the existing theory erroneous without our help.
We never asserted, that the inertial theory of a rotor dynamics is correct. On the contrary, we have addressees to all with the request to find mistakes in the inertial theory. Till now nobody has found out mistakes in the inertial theory. Experts IFToMM have burst in abuse, however have not found out lacks of the new theory.
We count premature to open practical value of the new theory in full. In the beginning everyone should realize, that the vibrating theory is unpromising. Pay attention that about 40 scientific papers of conference in Sydney begin with consideration of the traditional equation of the theory of oscillations. It means, that in a rotor dynamics there are unsolved problems for today.
In my opinion, the classical vibrating theory of a rotor dynamics is replaced with experimental data, which are processed by numerical methods. Thus, I count that in practice engineers use empirical dependences. Certainly, empirical dependences are received as a result of persistent scientific work. Certainly, empirical dependences yield good results at calculations. However, empirical dependences do not form the theory and have local application.
Any theory first of all has the academic value. Use of the theory for the solution of problems gives practical result. We hope, that we shall receive orders for the solution of practical problems.---Engineers frequently solve problems indirect methods or a trial and error method if the theory is absent. However these solutions are not optimum and in a consequence the engineers give new solutions on the basis of the theory.
We are not pleased with prospect of recognition of the inertial theory in 30-50 years.
The best regards, Yuriy Zhivotov
From: George
Prof! Allow asking, while Sasaki gets acquainted with the patent to explain
us circumstances of your invention and to fix connection of the invention
with the inertial theory. Your invention confirms, what vibrating theory
of rotor dynamics is erroneous? Regards, George.
From: Yu. Zhivotov
Dear George! About 20 years ago we were surprised, that in textbooks and
the technical literature there is no information, which can be operated
for a choice of parameters and calculation of the centrifugal stand. We
have found only the information on Jeffcott rotor. We have studied the
information on automatic balancing devices also.
The technical literature recommended us to operate two automatic balancing devices for dynamic balancing of a rotor. The technical literature recommended us to place balancing devices on both sides from a center of masses of a rotor. Such recommendations appeared erroneous and have resulted in increase of an unbalance of a disk rotor.
We have understood, that the vibrating theory of a rotor dynamics has problems with an estimation of behavior of a rotor, which has a static unbalance and a moment unbalance. We have understood also, that the vibrating theory does not understand influence of combinations of an equatorial and axial inertia moment on a rotor dynamics.
We have paid attention that the vibrating theory has no equation, which describes a rotor dynamics with a moment unbalance. Therefore 20 years ago we have been compelled to state new physics of rotation of a disk rotor and to create this invention. Simultaneously we have created the theory of automatic balancing of a rotor and have published this theory in the best magazines of the USSR. This theory can be operated in balancing laser machine tools or in balancing machine tools with pulse entering balancing masses.
The vibrating theory for 20 years could not take advantage of our achievements and could not describe a rotor dynamics with a static unbalance and a moment unbalance. Thus, we are compelled to recognize, that the patent the USA is the proof of weakness and an inaccuracy of the vibrating theory. The best regards, Yu. Zhivotov
From: GEORGE
Prof! You show, that existing rotor dynamics is described by the equation,
which describes oscillations of a tuning fork, oscillations of a beam
or oscillation of a load on a spring. Why you do not speak, what dynamics
of a children's rattle is similar to a rotor dynamics? Regards, George
From: Yu. Zhivotov
Dear George! Tell, why you had desire to make similar comparing? Dynamics of a children's rattle differs from dynamics of a load on a spring. Stones are inside a children's rattle. The best regards, Yu. Zhivotov
From: Yu. Zhivotov
DEAR COLLEAGUES! We take part in symposium ISCORMA-2. We managed to solve successfully all organizational and financial questions. It allows us to acquaint foreign scientists with the inertial theory of a rotor dynamics and to discuss this theory in a mode of dialogue.
On ISCORMA-2 the report, which will explain some circumstances of application of the theory for the solution of practical problems, will be made. These circumstances could not be described in a paper because of limitations on volume of the scientific article.
All news, as always, are published on the Site http://www.geocities.com/newrotor NEW THEORY OF ROTOR DYNAMICS: DYNAMICS OF UMBRELLA-TYPE ROTOR WITH FLEXIBLE SUPPORT.
ABSTRACT New inertial theory of the rotor dynamics has considerable opportunities to study a rigid body rotation with a single fixed supporting point. In this paper the rotation dynamics of a vertical umbrella-type rotor with a single flexible support and single fixed rigid support is described. Equations describing the rotation dynamics of a disk and cylindrical rotor are obtained.
Solutions of these equations are given. Dependencies to determine all forces and moments acting on a rotor are also obtained. Analysis of some equations and dependencies obtained from these equations is performed.
New solution of a classical problem of the theoretical mechanics about a body rotation around a single fixed point is obtained. New equations of the body rotation dynamics around a fixed point are obtained. The solution of these equations is found. Analysis of these equations and dependencies, obtained resulted from these equations, is performed.
1. INTRODUCTION 2. RESEARCH OBJECT AND COORDINATE SYSTEM 3. FORCES AND MOMENTS ACTING ON ROTOR 4. SYSTEM OF EQUATIONS OF ROTOR DYNAMICS 5. ANGLES DETERMING POSITION OF LINES OF ACTION OF THE FORCES 6. CYLINDRICAL ROTOR DYNAMICS 6.1 Dynamics of a cylindrical rotor with a single supporting point 7. DISK ROTOR DYNAMICS 8. DYNAMICS OF A DISK ROTOR WITH A SINGLE SUPPORTING POINT
The best regards, Yuriy Zhivotov
From: Malcolm Leader
Is solve some actual vibration problems using your theory that could NOT be solved using conventional rotor dynamics methods. Then people will pay attention. Until then, I'll go on solving problems with what has worked continuously for me for 25 years! Good Luck!
![]() About difference between Natural Frequency and Resonance Frequency
About difference between Natural Frequency and Resonance Frequency
I am very new to this vibration measurement. I have one basic question that what is the diference between natural frequency and resonance frequency of any object under vibration.
Thanking you vijayasiva, ([email protected]).
(http://www.vibinst.org/default.htm)
From: Arne
There is no difference. I can add the "eigen value" and the
"System resonance". You can consider resonance to be the result
of solving a math expression or as a result of interaction of real world
bodies and fluids with properties as weight, intertia, spring constant,
damping, etcetera. Pending the situation, one or more of the terms are
commonly used. This is a bit similar to the question if a glass filled
with 50 percent water is half full or half empty or has a 50 percent level.
I am happy you are interested in resonances in machinery. Wish you all
the best of luck in your studies. Regards Arne
From: E Murphy
Just adding a little on the subject Arne and Ron already answered: Suppose you have an electromechanical vibrator hooked to a power amplifier and a sine wave generator. If you excite a rotor for example, then the resonance frequency would be the one read at the sine generator when you have almost the largest amplitude (actual maximum peak is not at the natural frequency) Now, suppose you turn this rotor and increase speed. The "critical" speed will be the speed that matches the natural frequency of the rotor. In this condition it could have a different value than the first experiment. This could happen if, for example, the rotor has an overhung fan that could stiffen the "system" due to gyroscopic effects. With the exciter, the rotor would vibrate up an down if you apply it the center. While turning, the rotor will bow and will not vibrate up and down. The "high spot" will always be on the outside (assuming no other phenomena but unbalance) Hope this will not be confusing. Regards and good luck. E Murphy
From: Ron Hartlen
To improve your understanding of vibration fundamentals, and the real meaning of the technical words, there is a difference. A natural frequency is a PROPERTY OF THE SYSTEM, which depends primarily on mass and stiffness. There is no consideration of what's exciting it. When the system is forced to vibrate, and the forcing frequency is at or very close to a natural frequency, the response is strongly magnified. This condition of FREQUENCY MATCHING is called resonance. But as Arne says, for practical purposes, most people and trainers will call the system's natural frequencies the "resonant frequencies", even though it is confusing the fundamentals.
From: Yu. Zhivotov
Colleagues. I was possible also take part in conversation? I always thought, that natural frequency of oscillations of a beam could be received if to apply transverse force, and then to remove this force. However it is possible to cause to change a beam with any frequency with the help of transverse force if to put force with this frequency. Such oscillations of a beam refer to as the compelled oscillations. The beam caves in that upwards, downwards concerning a motionless axis of symmetry. Fibers of a beam are serially stretched and compressed. Critical frequency of oscillations of a beam is equal to frequency of natural oscillations. The resonance comes, if frequency of the compelled oscillations is equal to frequency of natural oscillations. At a resonance the amplitude of oscillations of a beam concerning a motionless axis of symmetry can grow beyond all bounds. The shaft of a rotor does not make oscillations. Fibers of a shaft do not test alternate compression and a stretching. However critical frequency of a rotor rotation will exist. Consider the equation (12) in a paper, which is published on the Site http://www.geocities.com/newrotor Natural speed of a rotor is defined, if the unbalance of a rotor e is equal to zero. The compelled speed of a rotor is defined from the equation (12) if cosine an angle it is equal 90 degrees. Concurrence of natural speed and the compelled speed result in a resonance. My reasoning almost reminds the theory of oscillations. However there is some difference. The best regards, Zhivotov.
From: The Shaker
I have always thought that the resonant frequency of a system is when the 'Forcing' frequency of this system equals the "Natural" frequency of the same system, the closer they are to unity the greater the amplitudes experienced! Regards
From: Yu. Zhivotov
Dear Shaker! I likely shall stay in minority. I think, that the resonance is the phenomenon, which arises if frequency of action of the compelled force on a beam coincides with frequency of own fluctuations of a beam. Moreover, the phenomenon of a resonance arises in vibrating system. In my opinion, the rotor rotates around of an axis of rotation, and the rotor does not vibrate concerning this axis. The beam is bent upwards and downwards serially concerning a neutral line under action of sign-variable force. Centrifugal force, which acts on a rotor, has one direction. Therefore the shaft is bent in one direction concerning an axis of rotation. Centrifugal force does not act on a rotor with any frequency. Centrifugal force is constant force on size on the given speed of rotation of a rotor. Therefore the phenomenon of a resonance does not arise at rotation of a rotor. At rotation of a rotor there is a phenomenon of an unlimited deflection of a shaft. When I look at a rotor from the side, it seems to me that it vibrates. However, it only seems to me. It is not present actually. The note: The stator really vibrates. Centrifugal force changes direction be relative of the stator. The best regards, Yu. Zhivotov
From: The Shaker
Why did the simple question about resonance suddenly become so complex?
If I knew what the dickens you were talking about I might be persuaded
to comment!
From: Yuriy
To The Shaker. Obviously you are right. Yuriy
From: S. Paul Mohan
In practical terms, one does not have to worry about each and every natural frequencies.. As said by others, a machine can have a lot of natural frequencies. But, they are not important as the machine does not resonate or vibrate on all the natural frequeccies. SO, RESONATION or HIGHER VIBRATION is the key. Resonate frequecies are more important,as machine responds at these frequencies. Mathematically, resonate frequencies area sub set of natural frequencies. Again, a simple explanantion, as in real life, the damping present changes natural frequecies and resonant frequencies.
![]() About "Viscous" friction
About "Viscous" friction
What means the term " Viscous" friction? What is understood as viscous friction?
Regards, Gennady
(http://www.vibinst.org/default.htm)
From: Ron Hartlen
In basic vibration theory, a viscous friction force is exactly proportional
to the vibration velocity, and acts in the opposing direction. Viscous
friction simplifies the mathematics. Pure viscous friction is rare, but
the damping in systems can be represented reasonably well by equivalent
viscous damping. A device providing damping by the shearing of fluid in
a gap, eg between plates, would actually be viscous.
From: George
Viscous friction is in more detail considered in the textbook " Vibration Problems in Engineering By S. Timoshenko. Viscous friction arises at motion of a body in air or in a liquid with small speed. External friction, which acts on a rotating rotor, is considered as viscous friction also. Regards, George.
From:
To give a practical example of viscous friction, when it is time to mix
the pan-cake batter, an experienced cook will never try to move the ladle
very fast. The reason for this is the faster you try to move the ladle
the higher will be the force on the ladle. Same is the principle of viscous
damping. The friction force is proportional to the velocity and is opposes
the velocity. And by definition damping force is a force that opposes
the velocity. Hence the above viscous friction effect is considered as
viscous friction damping in the context of vibration.
From: Gennady
All many thanks. George has guessed. I have found out the term viscous
friction in a paper on a rotor dynamics. However George has given an inconsistent
explanation. He speaks, that viscous friction does not act on a rotor
if the rotor rotates with high speed. In a paper, which I read, it is
not told about it of anything. There can be I have misunderstood him?
Why in the equation of a rotor dynamics viscous friction will be operated
if he is right? Regards, Gennady
From: [email protected]
As far as my knowledge is concerned, there is no limitation on speed in the context of viscous friction damping. The damping term in the SONLDEWCC of motion of a rotor consideres the damping to be viscous and constant over the entire speed range, which need not be true in the case of modern turbomachinery and the speeds (I am talking about frequency dependance of damping coefficient). In some cases the mechanism of damping is not viscous (like hysteritic or coulomb friction damping). In such cases the equivalent viscous damping coefficient is formulated from experiments and theoritical analysis to be used in the equation of motion.
From: Yuriy Zhivotov.
Dear all! In the theory of vibration there is a concept of viscous friction.
Viscous friction is the average value of aerodynamic friction for one
cycle of oscillations of a beam. It is considered, that force of friction
is proportional to average speed of transverse motion of a center of masses
of a beam at low speeds.
Actually speed of moving of a center of masses of a beam changes from zero up to the maximal value during one cycle of oscillations. In the theory of vibrations also there will be a concept of internal friction. Internal friction is associated to moving layers of a beam be relative each other at transverse oscillations of a beam. The vibrating theory of a rotor dynamics has automatically transferred achievements of the theory of vibrations on process of a rotor rotation. Automatic carrying is the next mistake of scientists, which are engaged in a rotor dynamics. (the Basic mistake has been admitted, when process of a rotor rotation have replaced with process of oscillations of a rotor). Automatic carrying has resulted in internal contradictions in the theory of a rotor dynamics.
For example. F.M.Dimentberg in the textbook " Dynamics of machines " pays attention that internal friction arises at oscillations of a beam as longitudinal layers of a beam are cyclically stretched and compressed serially at each cycle. F.M.Dimentberg enters internal friction in the equation of a rotor dynamics as oscillations of a rotor occur to a flexure of a shaft in one and in other side. Through some pages in F.M.Dimentberg's this book writes, that on supercritical speeds the rotor rotates the light side outside. It is possible in the event that the shaft rotates in a bent condition without hesitation. In this case longitudinal layers of a shaft serially are not stretched and not compressed. Hence, internal friction will not exist at a rotor rotation.
So, F.M.Dimentberg contradicts to itself. Let's consider external friction and its influence on oscillations of a beam and a rotor rotation. External friction creates force of frontal aerodynamic drag if there are oscillations of a beam concerning a neutral line. External friction creates force of superficial aerodynamic drag if the rotor rotates. It is necessary to note, that vibrating dynamics neglects this difference. I think, that it is wrong. Today the majority of rotors rotate with high speeds.
Therefore, external friction should be proportional to a square (as a minimum) speeds of rotation (It recommends S. Timoshenko). Therefore it seems to me, that the idea of viscous friction cannot be applied at the solution of problems of dynamics of real rotors. However the account of external friction in the equation of a rotor dynamics also brings the contradiction in the vibrating theory of a rotor dynamics. F.M.Dimentberg marks, that friction in bearings also creates external drag. However F.M.Dimentberg suggests to not taking into account influence of friction in bearings as the torque can compensate influence of friction. In my opinion the torque can compensate influence of superficial aerodynamic drag also.
Therefore I also want to know that is understood as viscous friction in the equations of a rotor dynamics (the vibrating theory). I think, that the vibrating theory of a rotor dynamics is not capable to answer this question. In the near future we shall make presentation of a paper where this question has found the solution. It is a paper it has been directed to China for presentation on congress IFToMM.
Sincerely, Yuriy Zhivotov.
![]() About Resonance
About Resonance
Dear Friends, I have a reonance problem in a vertical pump.It used Bump Test to confirm the same using CSI-RBMCONSULTANT when equipment was off. The resonant frequency is matching the rotational frequency of the motor. Now,My doubt is that what and all maintenance work should I do the equipment to bring down the vibration? is it K (STIFFNESS) OR M(MASS) only and how? The height of equipment is around 2.5 mtrs with flexible coupling. please give your suggestions?
REGARDS, MALLIK
(http://www.vibinst.org/default.htm)
From: Alex J
We had similar problem with a brand new pump. It was pointed out to the
manufacturer, who brough several consultans to confirm it. Finally a new
thicker plate motor support was fabricated and vibration dropped from
0.3 in/sec to 0.05 in/sec. If this is a new pump go back to the OEM.
From: E Murphy
Mallik: We have changed the resonance frequency of a couple of pumps by
installing pieces of tire (8, one every 45 degrees) between the pump lower
flange and the support base. The natural frequency dropped about 150 CPM.
On one pump we added mass at the top of the motor (about 400 kg) and the
frequency dropped about the same amount. These solutions are far more
easy to implement than adding stiffness. Regards E Murphy
From: [email protected]
Generally the vertical pump frequency tuning method is stiffness change
as motor stand thickness change, adding motor basebolt, inserting fablica
material between motor and motor stand, etc. But to apply the stiffness
change method have to sharp peak of resonance curve in FRF plot. If resonance
curver is wide and broad on operating frequency, You would like to apply
the vibration dynamic absorber system. Regards
From: Yu. Zhivotov
Dear MALLIK!
Frequency of natural oscillations of system can be reduced if to operate councils of dear E Murphy 7/28/03 and <http://www.vibinst.org/_vibezonenew/00001154.htm> Alex J 7/28/03. The councils will give positive result contrary to the vibrating theory of a rotor dynamics, which does not take into account influence not rotating affixed masses.
If second advice of E Murphy gives positive result you try the vibrating units to attach to a motionless basis through elastic lining.
I do not know the scheme of your machine in the collected kind and, hence, I cannot give effective advice.
However the new theory of a rotor dynamics shows, that the critical speed very much will depends from position of rotating details concerning support. You can change position of a center of masses of a rotating detail concerning supports?
The new theory of a rotor dynamics shows, that the critical speed very much will depends from position of a vector of a unbalance in a rotating detail concerning support. You can change position of balancing loads along an axis of a rotating detail?
Both ways allow to reduce critical speed of a rotor rotation approximately in one and a half time. I wish success. Yu. Zhivotov.
From: Willem
WE have experienced resonance problems with vertical pumps. most of the
time the top of the pump is vibration most (motor act as a rigid body).
Despite all theories the solution a often a simple as adding a bracket
between the top of the motor an a body (wall, other motor) nearby. In
other words: hold it tight. Regards Willem
From: Alex J
I would be careful with this solution. Have seen the walls completely
cracked because of it.
From: Malcolm Leader
Add Mass to the top. About 25% of the mass acting in the "reed" motion will work. Never needs maintenance; cheap. Trust me. Malcolm
![]() Issue of the research study financing
Issue of the research study financing
The rotor dynamics is issues of the day for the national economy sectors of Ukraine. However, research studies in this area have no adequate financing. This case had resulted in the need to seek a sponsor.
The Science and Technology Center in Ukraine (http://www.stcu.kiev.ua) had been found as such sponsor.
The STCU provides the various research projects with a financial support on a competitive basis, if a foreign firm, institute or corporation, etc. recognizes the project as necessary. Earlier, we addressed a request to analyze and confirm utility of the new rotor dynamics research project to a number of noted scientists.
It enabled us to ascertain that the scientific society wants first to become familiar with the underlying theses of new "inertial" theory.
We respected recommendations of the scientists and are participants in 6th International Rotor Dynamics Conference.
In view of this, we address to firms, companies, scientific institutions, universities, etc. for a request to analyze the project submitted to STCU competition, to appreciate it at its true utility, and to apply own considerations to STCU management.
At your assent, we forward you the project electronic copy immediately.