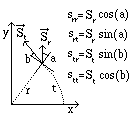Prev Up Top Next Contents
9.G Stabilita` delle cavita`
La stabilita` delle cavita` dipende da quattro fattori
[
916] [
917] [
918] [
919] [
920] :
- la resistenza alla rottura del materiale roccioso di cui sono fatte
le grotte;
- la presenza di discontinuita` (frattture, giunti di strato, faglie, ...);
- lo stato degli sforzi (stress) locale;
- le dimensioni a forma delle strutture ipogee.
Le condizioni geomeccaniche devono permettere l'evoluzione della
cavita` nel tempo.
La resistenza viene espressa in Kgp/cm2 o in
MPascal = 10 Kgp/cm2. Una altra unita` e`
ton/m2 = 0.1 Kgp/cm2.
Le rocce calcaree hanno valori di resistenza alla compressione dell'ordine di
900 Kgp/cm2 ed alla trazione di 50 Kgp/cm2.
La resistenza agli sforzi di taglio e` 125 Kgp/cm2.
Questi sono valori medi e bisogna tener conto che c'e` molta variabilita`.
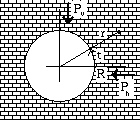
Fig. 392. Sforzi intorno ad una galleria
Lo stato degli sforzi nella roccia e` un tensore; un oggetto complicato.
Molto approssimativamente puo` essere considerato come una
composizione di due componenti di forza: una componente verticale
Pv, e una orizzontale Ph.
La componente verticale cresce con la profondita`, H,
proporzionalmente al peso specifico p della roccia:
Pv = p H, oltre a dipendere
anche dalla geomorfologia.
Il peso specifico delle rocce vale circa 2.5 Kg/l percio` il gradiente di
pressione e` circa 250-300 atm/Km.
Quella orizzontale e` determinata da spinte tettoniche (compressioni o
distensioni) e dalla ridistribuzione degli sforzi.
Il valore del rapporto fra le due componenti,
k=Ph / Pv, indica l'isotropia o meno
dello stato di sforzo.
A basse profondita` (meno di 500 m) sperimentalmente k
ha valori variabili fra circa 0.5 e 5.5. In profondita` si presume che
con la ridistribuzione degli sforzi k tenda ad 1
(condizioni idrostatiche).
In condizioni isotrope (k=1), lo sforzo tangenziale supera la
resistenza alla compressione a profondita` di circa due kilometri.
A basse profondita` in condizioni distensive, le cavita` possono
risultare instabili anche a poche centinaia di metri.
A basse profondita` (piccoli sforzi) predomina il comportamento
elastico della roccia per cui la stabilita` della cavita` e` determinata
dalla presenza di fratture e giunti.
Ad elevate profondita` (grandi pressioni) diventa rilevante
il comportamento plastico.
Le morfologie di crollo si distinguono in tre tipi:
- crollo a blocchi, di dimensioni superiori a quelle degli strati;
Questo e in genere associato a una stratificazione massiccia e a collassi
su grande scala;
- crollo a strati, con blocchi delle dimensione degli strati;
associato a strati non troppo spessi e con netti piani interstrato;
- crollo a pezzetti, con blocchi di piccole dimensioni. Dovuto alla
frammentazione dei blocchi caduti.
Frammenti di blocchi taglienti ed irregolari si notano negli ingressi delle
grotte alpine e sono dovute all'azione del gelo.
Il collasso naturale della volta avviene per progressivo cedimento delle
unita` [
921] . Gli strati cedono singolarmente oppure si staccano
dei blocchi cosicche` la volta rimane incurvata. E` un processo
rapido su scala geologica, se gli strati sono abbastanza sottili.
Una zona di compressione arcuata si sviluppa nel soffitto, generalmente
con altezza circa 1/3 della larghezza. Questo arco stabilizza la volta,
anche se la roccia e` fratturata. Pero` richiede uno sforzo compressivo
laterale, solitamente presente in profondita`, ma non vicino alla
superficie, dove la roccia si puo` rilassare ove non e` confinata.
9.G.1 Deformazioni
Per descrivere la stabilita` delle cavita`, cioe` la stabilita` della
roccia, bisogna ricorrere alla teoria degli sforzi nei mezzi continui.
Questa e` una branca abbastanza complessa della fisica matematica.
La ragione fisica risiede nel fatto che una forza applicata in una direzione
su un mezzo continuo puo` indurre sforzi (forze interne al mezzo) anche
in altre direzioni.
Per descrivere il problema si ricorre al calcolo tensoriale.
Vediamone gli aspetti generali.
Iniziamo con il formalismo per descrivere le deformazioni di un corpo
rigido. Per semplicita` limitiamo le formule a due dimensioni.
Un corpo subisce una deformazione (infinitasima) quando la porzione
al punto
u passa nel punto
u'.
Le caratteristiche della trasformazione possono essere descritte
in modo semplice in termini matematici quando la trasformazione e`
lineare
x' = a x + b y
y' = c x + d y
La trasformazione inversa, che dice da quale punto viene la porzione
del corpo che si trova nel punto (x',y'), risulta
x = ( d x' - b y' ) / D
y = ( a y' - c x' ) / D
dove
D=ad-bc e` il determinante della matrice
A
della trasformazione diretta.
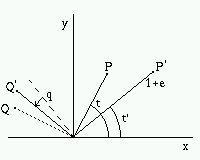
Fig. 393. Deformazioni
Nella trasformazione i segmenti vengono deformati e gli angoli
modificati. L'elongazione di un segmento e` legata al rapporto
fra la sua lunghezza dopo e prima della deformazione,
e dipende dall'orientazione del segmento
1 + e(t) = L' / L
La deformazione angolare descrive quanto un angolo retto si allarga
(positiva) o restringe (negativa).
Le direzioni vengono ruotate, tuttavia
ci sono due direzioni che restano immutate; sono gli assi principali
della deformazione. Se non ci sono dilatazioni o compressioni,
il corpo viene allungato nella direzione dell'asse
maggiore e schiacciato in quella dell'asse minore.
Per valutare elongazione, deformazione angolare e rotazione delle
direzioni si calcola come viene modificata una ellisse
A x
2 - 2 B x y + C y
2 = 1 dalla trasformazione.
Riportiamo solo i risultati finali [
922] .
Un segmento che forma un angolo
t con l'asse X dopo la deformazione
forma un angolo
t'
tan( t' ) = ( c + d tan(t) ) / ( a + b tan(t) )
tan( t ) = (c - a tan(t') ) / ( - d + b tan(t') )
La sua elongazione risulta
l = (1+e2) = ½(a2 + b2 + c2 + d2 )
+ ½(a2 - b2 + c2 - d2 ) cos(2t)
+ ( a b + c d ) sin(2t)
l'elongazione inversa
l' = 1/l = [ ½(a2 + b2 + c2 + d2 )
+ ½(d2 - b2 + c2 - a2 ) cos(2t')
- ( a c + b d ) sin(2t') ] / D2
Le direzioni degli assi principali sono quelle per cui l'elongazione
e` massima o minima,
tan(2t) = 2 (ab+cd) / ( a2 - b2 + c2 - d2 )
tan(2t') = 2 (ac+bd) / ( d2 - b2 + c2 - a2 )
Infine la rotazione degli assi principali risulta
tan( w ) ( c - b ) / ( a + d )
L'ellitticita` e` la radice quadrata del rapporto fra le lunghezze
dei due assi principali, R=(l
1 / l
2)
1/2.
La variazione (relativa) di area e` 1+d
A = ad - bd = D.
Infine la deformazione angolare e`
tan( q ) = [ 2 (ab+cd) cos(2t)
- a2 - b2 + c2 - d2 ) sin(2t) ] / (2D)
Le direzioni principali del tensore di deformazione determinano due
sistemi di linee ortogonali, campo di deformazione del corpo.
Queste linee terminano sulle zone non deformate con angoli di 45°
Per una trasformazione generica (non-lineare) si considera
l'approssimazione di primo ordine (cioe` la linearizzazione).
Il tensore
U di deformazione e`
dux/dx dux/dy
duy/dx duy/dy
ed e` legata alla matrice
A della trasformazione lineare,
A = 1 +
U.
9.G.2 Sforzo
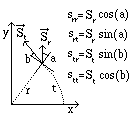
Fig. 394. Sforzo
Il tensore degli sforzi descrive lo stato delle forze che
agiscono all'interno del mezzo continuo. La componente
sik descrive la forza nella direzione
i
applicata su una superficie perpendicolare alla direzione
k
nel punto in esame.
Esso soddisfa due importanti relazioni. La
relazione di Cauchy, che discende dalla legge di Newton
applicata ai momenti torcenti delle forze, e che stabilisce che il
tensore degli sforzi e` simmetrico,
sik = ski
e la legge di Newton per la forze di volume
f,
fi = dk sik
Nel caso di un mezzo soggetto alla forza peso questa equazione diviene
dk sik = - d g,
dove d e` la densita`, e g la accelerazione di gravita`.
Il tensore degli sforzi deve soddisfare anche delle relazioni dovute
alle forze
F che agiscono sulla superficie del mezzo continuo,
precisamente le condizioni al contorno (o ai limiti).
Se
n e` il vettore normale alla superficie del mezzo, si ha
sik nk = Fi
Da sole queste relazioni non bastano a descrivere lo stato del mezzo
continuo. Ci vuole anche qualche relazione che lega gli sforzi alle
deformazioni, ed e` caratteristica del tipo di mezzo in esame
(mezzo elastico, mezzo plastico, etc.).
Prima pero` di completare le equazioni e risolvere lo stato di semplici
mezzi continui per arrivare ad una descrizione della stabilita`
delle cavita`, scriviamo queste relazioni esplicitamente in 2 dimensioni.
Il problema diviene bidimensionale in due casi: quando gli sforzi
sono piani, oppure quando le deformazioni sono piane.
Qui analizziamo il problema piano, cioe` ignoriamo completamente
la terza direzione. Questa e` una semplificazione e non corrisponde
ad alcuna delle due citate situazioni.
In due dimensioni (
x, e
y) l'equazione fondamentale e`
dx sxx + dy sxy = fx
dx sxy + dy syy = fy
In assenza di forze di volume (equazione omogenea) la soluzione piu` generale
e` espressa in termini delle derivate di una funzione,
X, detta
funzione degli sforzi:
sxx = dy2 X
sxy = - dx dy X
syy = dx2 X
Ruotando il sistema di coordinate di un angolo
t,
x' = x cos(t) + y sin(t)
y' = - x sin(t) + y cos(t)
il tensore degli sforzi diventa
s'xx = sxx cos2(t) + 2 sxy cos(t) sin(t)
+ syy sin2(t)
s'xy = ( - sxx + syy ) cos(t) sin(t)
+ sxy ( cos2(t) - sin2(t) )
s'yy = sxx sin2(t) - 2 sxy cos(t) sin(t)
+ syy cos2(t)
Scegliendo l'angolo in modo che s'
xy = 0, cioe`
il tensore ha solo le componenti principali, s'=diag(s
1, s
2),
dove
s1 = ½(sxx+syy) + sxy sin(2t) +
½(sxx-syy) cos(2t)
s3 = ½(sxx+syy) - sxy sin(2t) -
½(sxx-syy) cos(2t)
L'angolo
t e` una soluzione della equazione
tan(t) = 2 s
xy / (s
xx-s
yy).
Questa equazione ammette quattro soluzioni (fra 0 e 360°tuttavia esse sono equivalenti e corrispondono alle ambiguita`
di scelta (di 90°) degli assi.
Conviene introdurre le combinazioni
s+ = ½(sxx+syy)
s- = ½(sxx-syy)
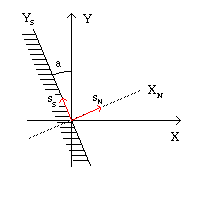
Fig. 395. Sforzo normale e di taglio
Le componenti normale, s
N, e di taglio,
s
S, dello sforzo lungo una
superficie la cui normale forma un angolo
a con il primo asse
principale degli sforzi, sono
sN = ½(s1+s3) + ½(s1-s3) cos(2a)
sS = - ½(s1-s3) sin(2a)
Attenzione: l'angolo
a e` l'angolo formato con le direzioni
principali del tensore degli sforzi, e queste non e` detto che
coincidano con gli assi orizzontale
x e verticale
y.
Dato che saremo interessati a soluzioni a simmetria cilindrica (cioe`
le gallerie) scriviamo queste relazioni usando le coordinate polari
| r = ( x2 + y2 )1/2
|
|
x = r cos(t)
|
| t = arctan( y / x )
|
|
y = r sin(t)
|
La trasformazione delle derivate (detta legge di trasformazione
covariante) risulta
| dx = cos(t) dr - sin(t)/r dt
|
| dy = sin(t) dr + cos(t)/r dt
|
| dr = cos(t) dx + sin(t) dy
|
| dt = - r sin(t) dx + r cos(t) dy
|
Le componenti del tensore degli sforzi si esprimono in termini di
quelle nel sistema di riferimento cartesiano (notate la similarita`
con le relazioni del tensore degli sforzi in un sistema di riferimento
ruotato di un angolo
t)
| srr = cos(t)2 sxx + 2 sin(t) cos(t) sxy
+ sin(t)2 syy
|
| srt = r (sin(t) cos(t) [syy-sxx]
- [sin(t)2-cos(t)2] sxy)
|
| stt = r2 (sin(t)2 sxx - 2 sin(t) cos(t) sxy
+ cos(t)2 syy)
|
L'equazione di equilibrio diventa
| dr( r srr ) + r-2 dt( r srt )
- r-2 ( r stt ) = fr
= r ( cos(t) fx + sin(t) fy )
|
| dr( r srt ) + r-2 dt( r stt ) = ft
= r2 ( - sin(t) fx + cos(t) fy )
|
In queste coordinate la soluzione dell'equazione omogenea si scrive
| srr = ( 1/r dr + r-2 dt2 ) X
|
| srt = ( 1/r dt - dr dt ) X
|
| stt = r2 dr2 X
|
9.G.3 Elasticita`
A basse profondita` nella roccia predomina il comportamento elastico,
per cui la stabilita` e` determinata dai punti di debolezza: fratture e
giunti (faglie e sovrascorrimenti).
Ad elevate profondita` gli sforzi sono piu` intensi e quindi interviene il
comportamento plastico. Si hanno cosi` le deformazioni, pieghe e
compressioni).
Lo spostamento dei punti del mezzo materiale soggetto allo sforzo, e`
il campo vettoriale u(x)
che descrive per ogni punto x di quanto si sposta in seguito alle
forze applicate: forze di superficie e forze di volume (eg, peso).
Il tensore di deformazione e` definito come
uik = (1/2) ( diuk + dkui ),
dove dk denota la
derivata nella direzione k. In realta` questa e` una approssimazione,
valida per piccoli spostamenti, che non tiene conto di termini di secondo
ordine.
In coordinate polari
| ur = cos(t) ux + sin(t) uy
|
| ut = - r sin(t) ux + r cos(t) uy
|
| ux = cos(t) ur - sin(t)/r ut
|
| uy = sin(t) ur + cos(t)/r ut
|
| urr = dr ur
|
| urt = 1/2 (dr ut + dt ur) - ut/r
|
| utt = dt ut + r ur
|
Un mezzo elastico e` determinato dalla relazione lineare fra il tensore
delle deformazioni e quello degli sforzi (legge di Hooke).
In due dimensioni (in tre dimensioni i coefficienti numerici sono
differenti) si ha
sik =
K ull aik + 2 U ( uik - 1/2 ull aik )
= L ull aik + 2 U uik
dove
ull =
u11 +
u22
e
aik e` la metrica (tensore metrico), che in
coordinate cartesiane vale
aik = diag(1, 1),
e in coordinate polari
aik = diag(1, r
2).
K e` detto modulo di compressione uniforme (o coefficiente di
dilatazione volumetrica) e
U e` il
modulo di scorrimento. Assumono valori sempre positivi.
Il secondo coefficiente di Lame e`
L = K - U.
La relazione inversa e`
uik = 1/(4K) sll aik
+ 1/(2U) ( sik - 1/2 sll aik )
Vediamo il primo esempio semplice: nel caso di compressione uniforme
sik = - p aik. Allora si ha
ull = -p/K e 1/K rappresenta la variazioni
relativa di volume al variare della pressione (a temperatura costante):
1/K = - 1/V dV/dp.
Si parla di deformazioni omogenee quando il tensore di deformazione
e` costante il tutto il mezzo. In tal caso anche il tensore degli
sforzi e` costante in tutto il mezzo.
La relazione fra i due tensori e` scritta in termini di due
nuovi coefficienti: il coefficiente di
Poisson
S = (K-U)/(U+2K), che rappresenta il
rapporto fra compressione trasversale e allungamento longitudinale,
e il modulo di trazione (o di Young
E = 6 K U / (U+2K),
| sik = E/(1+S) ( uik + S/(1-2S) ull aik )
|
| uik = 1/E ( (1+S) sik - S sll aik )
|
Questa tabella riporta valori indicativi del modulo di Young e del
rapporto di Poisson. Un rapporto di Poisson molto basso e` indice della
capacita` della roccia di accumulare sforzi senza subire deformazioni
(fino a che non si frantuma in maniera "esplosiva" a causa dell'elevato
rilascio d'energia).
| |
E (105 Kgr/cm2)
|
v
|
| marmo |
5.0 |
...
|
| calcite |
5.6 |
0.17-0.18
|
| granito |
5.9 |
0.11
|
| quarzite |
8.2 |
...
|
Scritte per esteso queste formule sono
| sxx = E/((1+S)(1-2S)) ((1-S) uxx + S uyy)
|
| sxy = E/(1+S) uxy
|
| syy = E/((1+S)(1-2S)) ( (1-S) uyy + S uxx )
|
| uxx = 1/E ( sxx - S syy )
|
| uxy = (1+S)/E sxy
|
| uyy = 1/E ( syy - S sxx )
|
In coordinate polari la relazione e`
| urr = 1/E ( srr - S r-2 stt )
|
| urt = (1+S)/E srt
|
| utt = 1/E ( stt - S r2 srr )
|
Le equazioni di equilibrio dei mezzi isotropi elastici si ottengono sostituendo
nella equazione fondamentale
dk sik = -
d gi
l'espressione del tensore degli sforzi in termini di quello di
deformazione e quest'ultimo in termini del vettore di spostamento.
D u + 1/(1-2S) grad div u = - 2(1+S)/E d g
Applicando l'operatore div a questa si ottiene
D div u = 0,
cioe` div u e` una funzione armonica.
Applicando l'operatore di Laplace,
D=dx2 + dy2,
si ha D D u = 0,
cioe` il vettore deformazione u e` una funzione biarmonica.
E` possibile anche esprimere la soluzione generale delle equazioni di
equilibrio in termini delle derivate di un vettore biarmonico arbitrario.
Nel caso bidimensionale senza forze di volume (caso omogeneo)
abbiamo sxx + syy = D X e
uxx + uyy = div u.
Quindi D D X = 0 cioe` X e` una funzione biarmonica.
La densita` di energia immagazzinata nelle tensioni interne al mezzo e`
En = uik sik
Per un messo elastico questa si scrive in coordinate polari
En = (1/2E) ( srr2
+ 2 (1+S) r-2 srt2
+ r-4 stt2
- 2 S r-2 srr stt )
9.G.4 Stabilita` delle cavita`
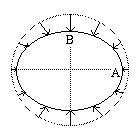
Fig. 396. Deformazione di compressione
Cominciamo vedendo cosa succede nella roccia piena, cioe` senza
cavita`. Come primo esempio prendiamo una compressione lungo i
due assi delle coordinate,
per un mezzo infinitamente esteso
La figura a destra mostra gli spostamenti dei punti su una circonferenza:
la circonferenza viene deformata in una ellisse.
In questo caso
uik = diag( A, B )
e il tensore degli sforzi e` pure diagonale,
sik = diag(P
H, P
V)
dove
PH e` la componente orizzontale della forza
di compressione e
PV e` quella verticale.
Risulta
| A = (1+S)/E ( S PV + (1-S) PH )
|
| B = (1+S)/E ( S PH + (1-S) PV )=
|
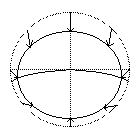
Fig. 397. Deformazione di compressione (anisotropa)
Come secondo esempio aggiungiamo la compressione dovuta
alla densita` del mezzo (cioe` una forza di volume diretta verso il basso).
| ux = A x - 2 C x y
|
| uy = B x + B' y2 + C x y
|
La figura a destra mostra gli spostamenti lungo una circonferenza
e lungo un asse orizzontale.
Anche in questo caso
uik = diag( A - 2 C y, B + 2 B' y)
e il tensore degli sforzi e` pure diagonale.
Se
B' = (1-S)/S
C esso ha la forma
sik = diag(P
H, P
V - d g y)
A = (1+S)/E ( S PV + (1-S) PH )
B = (1+S)/E ( S PH + (1-S) PV )
C = (1+S)/E S/2 ( -d g )
9.G.4.1 Gallerie
Consideriamo un mezzo con una cavita` circolare.
Questo rappresenta idealmente il condotto di una galleria
nell'ammasso roccioso.
Sulla superficie della cavita` deve annullarsi la componente
normale dello sforzo (in assenza di forze superficiali).
Conviene cercare la soluzione delle equazioni d'equilibrio, come
perturbazione alla soluzione del mezzo senza cavita` data dagli esempi
precedenti. Per semplicita` faremo riferimento al primo esempio.
ui = uoi + u'i
sik = soik + s'ik
La deformazione
u' soddisfa il problema omogeneo, percio`
s'ik si esprime in termini di derivate di una
funzione biarmonica generale, che si puo` scrivere come sviluppo
in serie di soluzioni indipendenti.
La condizione di annullamento all'infinito limita il numero
dei termini della serie (somme su
k>1),
X = ao log(r)
+ ∑ak r-k cos(k t)
+ ∑bk r-k sin(k t)
Per le condizioni al contorno (annullamento della componente normale
dello sforzo
srr) si ha
s'rr = - sorr
= - (PH + PV)/2 - (PH - PV)/2 cos(2t)
Conviene introdurre due combinazioni delle pressioni,
P+ = ( PH + PV) / 2
P- = ( PH - PV) / 2
Calcolando la componente
s'rr si ottiene che solo
due coefficienti di
X non sono nulli,
ao = -
P+ R2, e
a2 = 1/6
P- R4,
dove
R e` il raggio della cavita`.
Le componenti del tensore degli sforzi risultano
| srr = P+ ( 1 - [R/r]2 )
+ cos(2t) P- ( 1 - [R/r]4 )
|
| srt = - r sin(2t) P- ( 1 + [R/r]4 )
|
| stt = r2 P+ ( 1 + [R/r]2 )
+ r2 cos(2t) P- ( -1 + [R/r]4 )
|
La resistenza alla compressione della roccia
e` circa 900 Kgp/cm
2,
quella alla trazione 50 Kgp/cm
2
e quella a sforzi di taglio 125 Kgp/cm
2.
La pressione
PV e`
data dalla pressione idrostatica,
d g H, dove la densita`
della roccia e` circa 2500 Kg/m
3.
La pressione orizzontale e` dell'ordine di quella verticale,
potendo essere sia maggiore (se prevale la componente compressiva)
o minore (componente distensiva).
La condizione di stabilita` richiede che la componente tangenziale del
tensore degli sforzi non ecceda la resistenza della roccia alla compressione,
e quella di taglio non ecceda la resistenza agli sforzi di taglio
(PH + PV) <900 Kgp/cm2
(PH - PV) <125 Kgp/cm2
Prendiamo in esame la roccia soggetta a sforzi compressivi.
Assumendo che le pressioni orizzontale e verticale hanno lo stesso
ordine di grandezza, risulta che e` il primo vincolo a determinare la
stabilita` delle cavita`, le quali
sono possibili fino a profondita` dell'ordine di 1800 m.
Questa stima e` in accordo con i dati geofisici sulla presenza di cavita`
fino a profondita` di alcuni kilometri.
In condizioni anisotrope il secondo vincolo diventa importante.
Con i valori di K riportati sopra,
la profondita` limite e` ridotta all'ordine di poche
centinaia di metri.
Se c'e` una pressione interna nel condotto (galleria in regime freatico
allagata), la condizione al contorno diventa l'egualianza della
componente radiale del tensore degli sforzi con la pressione
idrostatica del fluido,
srr = Pi.
Analiticamente bisogna rimpiazzare P+ con
P+ - Pi.
Quindi risulta che il fluido aiuta a sostenere con la sua pressione
la galleria, come ci si aspetterebbe intuitivamente.
L'acqua produce una spinta idrostatica pari al suo peso specifico,
1 t/m
3. Se il livello dell'acqua scende di 10 m lo sforzo
effettivo aumenta di 10 t/m
3 [
725] .
9.G.4.2 Pareti
Consideriamo ora lo sforzo su una grande parete ammettendo sempre che a grande
distanza il tensore degli sforzi abbia la forma diagonale
so = diag( P
H, P
V).
Per semplicita` supponiamo che la parete sia infinitamente estesa e
il mezzo continuo occupi le regione
x >0.
Come sopra cerchiamo la soluzione della equazione omogenea, che si esprime in
termini di derivate della funzione degli sforzi,
X, che si
puo` scrivere come integrale
X = Int [ ak e- |k| x - i k y ] dk
in cui i coefficienti
ak sono determinati dalle
condizioni al contorno, cioe` dall'annullarsi della componente
sxx sul piano
x=0.
Se prendiamo che
sxx1 deve compensare
una pressione orizzontale
PH, risulta
X = PH (x2 - y2)/2
per cui il tensore degli sforzi globale, nelle vicinanze della parete,
risulta avere solo la componente
syy = P
H + P
V.
La presenza della parete porta alla concentrazione degli sforzi
(nella direzione tangenziale). In realta` abbiamo ricavato questo
risultato per una parete infinitamente estesa.
In pratica la parete e` finita ed allontanandosi da essa il tensore degli
sforzi ritorna ad essere
so.
9.G.4.3 Saloni
Quale ultimo esempio riportiamo i risultati per la cavita` sferica
(in tre dimensioni, cioe` una grande sala) dal libro
L. Landau, Liftschitz, "Teoria della elasticita`", ed. MIR ...
p. 37.
L'espressione finale del tensore degli sforzi risulta
sik =
qoik (
1 + 5(1-2S)/(7-5S) r-3 + 3/(7-5S) r-5 )
+ 15/(7-5S) r-3 [S - r-2]
( qoil nk nl
+ qokl ni nl )
+ 15/2(7-5S) r-3 [-5 + 7 r-2]
qolm nl nm
ni nk
+ 15/2(7-5S) r-3 [1 - 2S - r-2]
qolm nl nm
aik
+ 1/3 qoll [ aik + 1/2 r-2
( aik - ni nk ) ]
dove q
o e` il deviatore degli sforzi, che in tre
dimensioni si scrive
q
oik =
s
oik - 1/3 s
oll
a
ik .
Sulla superficie della cavita` gli sforzi diventano
sik =
15/(7-5S) [ (1-S) (soik
- soil nk nl
- sokl ni nl )
+ solm nl nm
ni nk
- S solm nl nm aik
+ (5S-1)/10 soll
( aik - ni nk ) ]
Risulta che nelle vicinanze della cavita` gli sforzi sono molto piu`
intensi che nelle lontananze. Questo incremento degli sforzi ha carattere
molto pronunciato e diminuisce rapidamente con la distanza
(fenomeno di concentrazione degli sforzi nei pressi delle cavita`).
9.G.5 Plasticita`
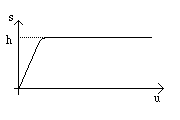
Fig. 398. Plasticita`
Un mezzo continuo ha un comportamento elastico fintanto che lo sforzo non
eccede un certo limite. Quando tale limite viene raggiungo il mezzo diviene
plastico e, se le regioni circostanti e i vincoli lo consentono, fluisce
subendo deformazioni sempre maggiori.
La figura a fianco mostra la relazione fra lo sforzo s e lo
scorrimento u. Il valore h e` la costante di plasticita`
del mezzo.
L'equazione che descrive il comportamento plastico e` la relazione che lega
il tensore degli sforzi ad
h. Introducendo il deviatore degli
sforzi,
| qik = sik - ½sll aik
|
| sik = qik + ½sll aik
|
che ha
qll=0, la relazione e` (scritta in termini del
tensore degli sforzi e del deviatore degli sforzi)
(sxx - syy)2 + 4 sxy2
= 2 h2
(srr - stt/r2)2
+ 4 srt2/r2
= 2 h2
q112 + 2 q122
+ q222 = 2 h2
Il legame fra sforzi e la velocita` v degli
scorrimenti in condizione plastiche pure, cioe`
senza elasticita`, e` qik = L vik
dove L e` un coefficiente di proporzionalita` e
vik e` il tensore delle velocita` di deformazione
vik = ½( di vk + dk vi )
Il fatto che qll=0 implica che div v=0,
cioe` non c'e` variazione di volume in assenza di elasticita`.
Percio` in condizioni plastiche si hanno due equazioni di equilibrio
(tra le forze di volume e le derivate del tensore degli sforzi), e una
relazione algebrica (fra le componenti del tensore degli sforzi).
Le equazioni della dinamica diventano D vk = fk.
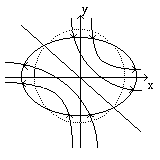
Fig. 399. Deformazioni plastiche
Come esempio consideriamo uno spostamento plastico con deformazione, ma
senza variazione di volume, in assenza di forze di volume.
| v1 = cos(a) x + sin(a) y
|
| v2 = - sin(a) x + cos(a) y
|
per cui risulta
| v11 = cos(a)
|
| v12 = sin(a)
|
| v22 = - cos(a)
|
Nella figura a destra e` schematizzato il movimento del mezzo plastico.
Non si ha scorrimento sulla linea diagonale.
Nella parte sopra di essa a destra si ha un flusso verso il basso. In
quella inferiore sinistra uno verso l'alto. Alcune linee di flusso
sono indicate.
L'angolo di intersezione delle linee di flusso con gli assi e` a.
Un cerchio viene deformato in una ellisse.
9.G.6 Crolli
I crolli sono classificabili in base alla dimensione dei massi:
- a blocchi, in cui i massi provengono da piu` strati;
- a strati, consistenti di pezzi di singoli strati;
- a frammenti, piccoli pezzi di roccia (cm - dm).

Fig. 400. Crollo di blocchi
Quando lo stato degli sforzi si dispone attorno alla cavita` secondo
quanto visto sopra, gli strati all'interno della superficie di sforzo
radiale nullo sono soggetti al solo sforzo dovuto al loro peso.
In queste condizioni uno strato e` come una sbarra appoggiata sui due
estremi, oppure come una trave infissa da una parte in un muro.
La teoria della elasticita` permette di valutare lo spessore minimo
sotto il quale si ha crollo dello strato.
La deformazione dello strato e` approssimativamente una flessione nella
direzione verticale. Denotiamo con
L la larghezza (ovvero la sporgenza)
dello strato e con
h lo spessore.
Supponiamo che sia molto lungo, in modo da trascurare
le variazioni nel senso della lunghezza.
L'equazione che descrive la flessione
z e`
D2 z = 12 (1 - s2) d g / (E h2) = R
(l'operatore differenziale e` il quadrato del Laplaciano).
Nelle nostre condizioni semplificate
z=z(x) con condizioni
all'estremo
x=0 definite da
z(0)=0 e
dz(0)=0.
Le condizioni all'altro estremo,
x=
L, dipendono se lo strato
appoggia alla parete oppure no. Nel primo caso sono come quelle
in
x=0; nel secondo sono
Dz(
L)=0 e
dDz(
L) = 0, cioe` l'annullamento del Laplaciano e della
sua derivata.
In questo secondo caso (strato infisso) risulta
z(x) =
R/24 (6
L2 x2 - 4
L x3
+
x4 ), e lo sforzo
sxx =
E/(1-
s2)
uxx risulta
sxx = 6 d g z h-2 (L - x)2
Il valore massimo dello sforzo si ha per
x=0, e per la stabilita` deve
essere inferiore alla resistenza
S della roccia.
Risulta quindi che lo spessore deve essere
h >3 d g L2 / S
Nel caso di strato appoggiato alle due pareti, risulta
z(x) =
R/12 (
L2 x2 -
L x3
+
x4/2 ) e lo spessore minimo per la stabilita` e` un terzo
che nel caso precedente
h >d g L2 / S
Uno strato di 50 cm di calcare puo` essere ampio fino a 25 m se appoggia
ai due estremi, e solo fino a 10 m se appoggia ad un estremo.
Uno strato spesso 5 m arriva difficilmente ad una ampiezza di 30 m
se sostenuto ad un solo estreno [
725] .
I soffitti tendono ad assumere una forma arcuata che permette di
distribuire gli sforzi e risulta percio` piu` resistente al collasso.
In pratica il crollo avviene per cedimenti strutturali della roccia.
Questo modello non tiene conto delle deformazioni plastiche
e della evoluzione delle microfratture.
Secondo la teoria di Tharp queste si propagano con velocita`
v = c (Ks / Kc)n
dove
Ks e` l'intensita` dello sforzo
(in Mpa/m
1/2),
Kc e` la resistenza alla
fratturazione della roccia, e
c e` una costante connessa alla
energia di attivazione.
La porosita` e la presenza di vacuoli agiscono come fattori inibitori
per la propagazione delle microfratture.
Il tempo di propagazione delle fratture va da alcune migliaia d'anni al
milione d'anni, ed e` quindi dello stesso ordine di grandezza del
tempo di evoluzione dei passaggi, percio` un crollo puo` aver luogo
in ogni istante, anche senza che intervengano altri processi ad
iniziarlo.
I processi che possono iniziare un collasso sono
- instabilita` meccanica dovuta all'allargamento della cavita`;
- passaggio da condizioni freatiche a condizioni vadose: la spinta
archimedea controbilancia il peso per circa il 42
- dissoluzione di fratture causata da un regime di
allagamento alternato;
- allargamento delle fessure, dovuto allo scorrimento di acqua;
- azione del gelo;
- forze distensive dovute a ricristallizzazione.
9.G.7 Dislocazioni
...
marco corvi - Mon Nov 19 11:34:13 2007
Prev Up Top Next Contents
This work is licensed under a Creative Commons
Attribution-NonCommercial-ShareAlike 2.0 Italy License.