

O Violão
O violão é um instrumento de corda, em sua maioria possuí 6 delas de diferentes espessuras mas de mesmo tamanho.
Porém existem violões de 6, 7 e 12 cordas que podem ser de nylon ou de aço. Tomaremos como base e exemplo o violão clássico: 6 cordas de nylon.
O violão é formado por diversas partes e por diversos materias. Veja na figura que se segue
 |
|
O violão é um instrumento de cordas que quando essas cordas sofrem uma perturbação elas emitem ondas sonoras. Essas ondas possuem algumas características que as diferenciam de outras ondas. São elas Intensidade, Altura e Tímbre.
A intensidade está relacionada ao tamanho da amplitude da onda, ou seja, refere-se ao volume daquele som. Podemos perceber uma diferença de intensidade no violão quando tocamos ele mais fraco e quando tocamos ele forte, assim estamos mudando a intensidade de seu som, ou seja, o volume.
A altura refere-se à freqüência com que esse som é emitido. Quanto maior for sua freqüência, mais alto é o som (agudo), e quanto menor a freqüência menor é a altura do som (grave). No violão existem cordas de diferentes expessuras, a corda mais grossa é mais grave, por isso tem uma pequena altura, e a corda mais fina possuí um maior altura, um som mais agudo.
O tímbre é o que podemos chamar da identidade do som, poís com ele podemos distinguir dois sons de mesma Intensidade e Altura. Ou seja se emitirmos um som em um violino e em um violão, mesmo tendo Freqüência e Volumes iguais, podemos distinguir qual é o som do violino e qual o som do violão pois cada intrumento possuí um tímbre diferente.
O Funcionamento
O violão convencional possuí 6 cordas de mesmo tamanho e espessuras diferentes. Para a afinação padrão de um violão essas cordas são tensionadas até um certo ponto, esse ponto é determinado pelo seguinte padrão:
MI (82,4hz) ; LA (110hz); RE (146hz) ; SOL (195hz) ; SI (246hz) ; MI (329hz) - corda mais grossa para a mais fina
Ao tocarmos o violão vibramos essas cordas nessas frequências. O vibrar da corda vibra o ar a que rodeia criando a onda sonora. Porém no violão temos o corpo que também é reconhecido como caixa de ressonância que possui um formato em 8. Devido a esse formato, semre há regiões da caixa que entram em ressonância com cada som emitido pelas cordas, amplificando-as tornando os sons fracos emitido pelas cordas em sons fortes.
A Física
O violão, assim como os demais instrumentos de corda, se constitui basicamente em cordas esticados e presas em ambas as extremidades. A perturbação produzida em um ponto qualquer entre os extremos de uma corda propaga-se para as duas extremidades. Nas extremidades, as perturbações são refletidas e voltam em sentido contrário sucessivamente. Temos portanto, a formação de uma onda estacionária.
A freqüência das ondas sonoras que as cordas emitem, dependem de três fatores: a densidade linear das cordas (µ), o módulo da tração a que elas são submetidas (F) e o comprimento da corda (L).
A densidade linear é calibrada pelos fabricantes dos encordoamentos. A tração é regulada com as cravelhas, que é o que o violonista faz quando afina o instrumento. O comprimento da corda varia conforme se pressionam as cordas com os dedos contra o braço do instrumento.
A menor freqüência de vibração, chamada freqüência fundamental ou primeiro harmônico da corda, corresponde à maneira mais simples de a corda vibrar, com nós nas extremidades fixas e um ventre intermediário.
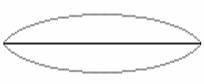
L = λ/2
Se essa onda tem comprimento λ = 2L e freqüência f = v/λ, logo f = v/2L.
O segundo modo de vibração constitui o segundo harmônico da corda e corresponde à presença de mais um nó e mais um ventre entres as extremidades da corda.
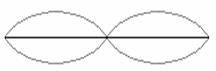
L = λ
Se o segundo harmônico tem comprimento de onda λ = L, a freqüência do segundo harmônico é f = v/L.
A cada novo modo de vibração, acrescem-se mais um nó e mais um ventre entre os extremos da corda. Assim, para o harmônico de ordem N, teremos comprimento de onda e freqüência dados por:
λ = 2L/N f = N.v/2L
A velocidade de propagação de uma onda transversal na corda é determinada por
onde F é a tração a que fica sujeita a corda, e µ é a densidade linear ( massa por unidade de comprimento.)
Logo, em função da tração na corda e da densidade linear, a freqüência é:
Por esta expressão, podemos entender como se produz uma melodia com um instrumento de corda. São três variáveis. Durante a execução, o músico controla o valor de L, porção vibrante da corda, ou muda de uma corda mais grossa para uma mais fina, alterando o µ. Para fazer a afinação do instrumento, ele controla a intensidade da força de tração por meio de roscas especiais (cravelhas). É assim que ele obtém as várias notas (freqüências).
Exercícios Resolvidos
1 . Uma corda de um violão oscila com um comprimento de onda de 60 cm. Os três menores valores possíveis para o comprimento da corda, em cm, são:
- 30, 60 e 90
- 30, 60 e 120
- 60, 90 e 120
- 60, 120 e 240
- 120, 180 e 240
Resolução
λ = 2L/N N = 1 è 60 = 2L/1 L = 30 cm
N = 2 è 60 = 2L/2 L = 60 cm
N = 3 è 60 = 2L/3 L = 90 cm
R. Letra “A”
2 . As cordas de um violão têm comprimento L. Nessas condições a primeira corda, que chamaremos mi1, deve ter freqüência fundamental de aproximadamente 660 Hz, enquanto a sexta corda mi2, deve estar um oitava abaixo, ou seja, sua freqüência fundamental deve ser de aproximadamente 330 Hz. Qual a razão entre as densidades lineares μ1/μ2 dessas cordas, supondo que ambas estejam submetidas à tração de mesmo módulo F?
R. ¼
3 . Uma corda de um violão tem 5g e 1 m de comprimento, tem a tensão de 968 N. Ache a velocidade das ondas transversais no fio.
V = raiz de força sobre mi! Mi = comprimento sobre massa!μ = 0.005/1 V = √968/0.005 Resposta: 440m/s
μ = 0.005 V = √193600
V = 440
4 . Se a freqüência do 3º harmônico numa corda vibrante de comprimento 1,2 metros é 150 Hz e sua massa é de 240 gramas determine com que velocidade as ondas se propagam ao longo dessa corda.
F = Nº de harmônicos ∙ V / 2L
150 = 3V / 2 ∙1.2
150 = 3V / 2.4
3V = 360
V = 360 / 3
V = 120 m/s5 . Uma corda de violão, tem 0,8 m de comprimento e a massa de 3 g. A corda está tensionada por uma força de 600 N. Qual a velocidade das ondas transversais na corda?
Resolução:
D = M/C V= √T/D
D = 0, 003/ 0,8 V= √600/ 0, 00375D= 0, 00375 V= √160 000
V= 400M/SExercícios para Resolver
1 . Uma corda de violão de 1 m de comprimento e densidade linear 1,0 · 10–5 kg/m tem suas extremidades fixas. Determine a freqüência do primeiro harmônico emitido pela corda quando submetida a uma força de tração de intensidade 6,4 N.
2 . Um fio de aço, de 5g e 1 m de comprimento, está fixo nas duas extremidades e tem a tensão de 632 N. Achar a velocidade das ondas transversais no fio. Achar o comprimento de onda e a freqüência da fundamental. Achar as freqüências do segundo e do terceiro harmônicos.