The system dynamics is expressed in so called “orbital” system of coordinates (that is: Cartesian rotating system, linked to the rocket and to the center of Earth). This system is non-inertial (rotating) therefore centrifugal and Coriolis accelerations have to be introduced.

The basic system dynamics is:

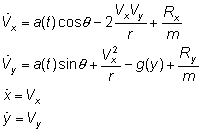
where:

a(t) – characteristic acceleration

r – distance to the center of the Earth

m – mass of the rocket

q – pitch angle

R – aerodynamic force

Discretization of the differential equations is done with the simplest Euler’s scheme.

Environment model

The Earth surface and gravitational field are assumed to be spherical. The linear velocity due to the Earth rotation (in the orbital plane) is calculated for the start location from its latitude and orbit inclination. Standard (international) model of atmosphere is used.

Used constants:

Grav. acceleration (polar): 9.83 m/s²

Earth radius: 6378 km

Gravitational parameter of Earth (m) 3.9893*10¹⁴m³/s²

Air density (sea level): 1.29 kg/m³

Launcher model

For each stage the following data has to be provided:

full mass (kg)

empty mass (+pressurization gas mass)* (kg)

specific impulse at sea level (s)

specific impulse in vacuum (s)

thrust (t)

Besides, for the entire rocket, the following data has to be provided:

payload mass (kg)

fairing mass (kg) and time of fairing jettison (s)

typical a/d areas (m²) and a/d coefficients (see. section “Aerodynamics”)

Fuel consumption is assumed constant (in the absence of throttling – see below). Thrust is calculated in the assumption that Isp dependency on the external pressure is linear (changing from от Isp_atm to Isp_vac).

(*) As fuel and oxidizer tanks are emptied, in order to maintain a nominal pressure, they should be filled with so called pressurization gas. For different rockets the pressure and chemical composition of the gas could be different, sometimes the exhaust products are used for this purpose. But, regardless of the details, the pressurization gas mass could be significant and should not be neglected. It should be included into the empty stage mass.

Aerodynamics

In the simplest case, for symmetrical body, drag force is directed along the axis of symmetry and determined by the well-known formula:

However, at nonzero attack angles the picture becomes more complex; the lift force emerges, etc.

The problem of precise aerodynamic force measurement is very difficult and for bodies of a complex shape can only be resolved through direct experiment (usually in wind tunnels). Solution is presented in the form of experimental tables or approximating curves.

The following model is often used as an approximation. It satisfactory estimates aerodynamic force for relatively small (to ~15 degrees) AOA.

(*) Note, that as rocket’s velocity is significant, we can neglect the viscose friction.

In velocity system of coordinates (i.e. system, linked to a velocity vector):

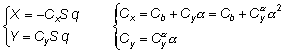
where:

a – angle of attack (angle between the axis of the rocket and velocity vector)

We will use trigonometric representation of this model in linked (to the body’s axes) system of coordinates:

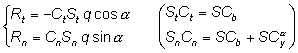
where:

R_t, R_n - a/d force projections of the body’s axes (main and side)

S_t, S_n - body’s typical areas (front and side sections)

(**) Usually values of a/d coefficients are taken for the same area (wing), but here we will use two different areas: frontal section area (typical area for the drag force) and area of the side section (typical area of the lift force).

It is easy to see that both representations are identical up to o(a²).

Throttling

It’s easy to see that with stages of the rocket working sequentially, the optimal mode is the one in which the engines always work at the full throttle. Then so called gravitational losses are minimal.

However, if at some moment stages must work simultaneously (usually, the first and the second), then it is usually more advantageous to reduce the fuel consumption of the second stage (during this phase). Such reduction of the fuel consumption (and the thrust) is called throttling.

The choice of the optimal throttle program covered with more details in: ”Optimal Control for Orbital Launcher” . In particular, it can be shown that, under certain assumptions, the optimal thrust program is piecewise-constant and consists of intervals of minimal and maximal thrust.

The spreadsheet allows for an arbitrary piecewise-constant thrust program.

User manual

The spreadsheet consists of several worksheets:

Main - The main page. Contains the input and output data

Simulation - Discrete simulation. Each line contains the system state at a certain time

Control - Several control (pitch) programs (see below). Each line contains control parameters at a certain time

Launchers - Data for some real launchers

Let’s start from the main page:

Launcher

Mass and thrust

For each stage, the corresponding column (I, II, III, IV) are filled with the following data:

full (fueled) stage mass

empty (dry) mass*

engines’ specific impulse (at sea level and in vacuum)

thrust in vacuum.

From this, fuel consumption is calculated automatically.

(*) As noted earlier, stage’s dry mass should include the mass of pressurization gas.

Also, the following data should be placed in the corresponding cells of the “Launcher” section:

payload mass

fairing mass (if any)

time of the fairing jettison.

From this, full launch mass is calculated automatically.

Aerodynamics

Aerodynamic parameters are set, in the corresponding column, for each stage*:

characteristic areas - S_x (frontal section) and S_y (horizontal section)

aerodynamic coefficients - C_x(drag) and C_y((lift).

Note that a/d coefficients C_x and C_y are set for system of coordinates, linked to the body axes. Above, in the description of the a/d model, they were designated as C_t and C_n respectively.

(*) To be precise, a/d parameters are set not for the rocket stage per se, but for the whole rocket during the period of the given stage work. I.e. in the first column we set a/d parameters for the rocket in the launch configuration, in the second – rocket’s parameters after the first stage separation, etc. If parameters are not set for some stage then they be considered zero for the corresponding period.

Thrust and throttling

By default, engines of the each next stage are fired immediately after the previous stage separation and work at full thrust.

More complex (piecewise-constant) program can be specified in the section “Throttle”.

The first column contains times of thrust change (in seconds). These values determine the intervals of constant thrust.

The columns that correspond to each stages determine the thrust (in percents) for the given stage during the given interval.

There are examples of different thrust programs in the section “Launchers” – notably, for the “Soyuz” and “Space Shuttle” launchers.

Please note the following:

Empty cells in thrust program correspond to the default program
The current stage always works at full thrust. Throttling is programmed only for the higher stages.
The time value t₀=0 can be omitted (see examples).

Also, if the provided capabilities are still not sufficient, there is a possibility of direct thrust programming. For that one has to reprogram the “Throttling” columns in the “Simulation” worksheet.

Spaceport and target orbit

“Spaceport” section contains the geographic parameters of the launchpad that affect the initial position and velocity of the rocket (latitude and altitude). The speed due to the rotation of Earth is calculated automatically. Initial velocity and its direction also can be specified (this may come handy for the airplane-based launch).

“Orbit” section contains parameters of the target orbit: altitude of the perigee/apogee and equatorial inclination. This data is then used for calculation of selected parameters of the orbit.

Data in the “Orbit” section is mainly of referral nature and does not affect the calculation of the trajectory – with one exception: inclination of the orbit combined with the lauchpad latitude determines the azimuth of the launch (the direction in which the rocket is launched). This value, in turn, determines the extent to which the rotation of the Earth “helps” the rocket. More precisely, the projection of the linear speed of the launchpad on the orbital plane is calculated in the cell “Earth rotation velocity” of the “Orbit” section.

Output

Section “System parameters” contains selected system parameters at the given time t. Moment t can be set arbitrary, by default it coincides with the last stage’s engine cutoff.

CV characteristic velocity

V velocity

V_x horizontal velocity

V_y vertical velocity

H altitude

stage current stage number

CV reserve current reserve of CV

mass mass

pitch pitch angle

Section “by stage” gives the same parameters at the moments of stage separations (times of the separations are determined automatically).

Section “Orbit” contains some parameters of orbit attained by the moment t (using t from the section “System parameters”).

Control

The rocket trajectory is controlled through the change of the pitch angle (the angle between the rocket main axis and the local horizon). The optimal choice of the pitch program is a quite complex problem. For more details see: ”Optimal Control for Orbital Launcher”.

Here we will call pitch control “optimal” if it delivers payload to the given altitude with given (usually, zero) vertical velocity and maximal horizontal velocity.

The spreadsheet supports following control models:

Linear - Piecewise-linear model

AOA + Linear - Angle of Attack + Linear model

A/d Drag - Aerodynamic model (drag only)

A/d Drag+Lift - Aerodynamic model (drag and lift)

To choose a model, enter symbol + next to its name (to the left) and remove symbol + from all the other models.

Detailed description of the models is given below. It is recommended for the inexperienced users to use the simplest (piecewise-linear, with one control interval) control program.

Control intervals

To define any control program one should start with defining one or several time intervals. On each such interval control program may have different parameters (piecewise control).

In the most cases, one interval (the entire active phase) is sufficient; however it may be useful to have several control intervals.

Control intervals are defined in the row t_i of the “Control” section. In the simplest case this row contains only two values: start (t₀=0) and end (different for each rocket) of the active phase.

Piecewise-linear control

In this program, during each control interval, tangent of the pitch is a linear function of time. Therefore, to define a program it is sufficient to define the pitch values q(t_i) in section “Pitch program/Linear”.

In the simplest case we define only one control interval, initial and final pitch values. Combined with the initial pitch restriction (see above) this model works quite satisfactory for the most of the vertical-launching rockets.

Note that in the vacuum linear pitch program is optimal. It is often used for the upper stages of the real rockets. As a rule, using any other control program makes sense only during the atmospheric stage of the ascent.

Note also that here we speak of linear dependency not of a pitch angle itself but rather of its tangent.

AOA+linear

The restriction on the angle of attack a (the angle between the main axis and the velocity) is often imposed on the atmospheric part of the trajectory. When the dynamic pressure is high, large angle of attack may lead to excessive load on rocket’s structure and, ultimately, to its destruction. In reality, in the atmosphere, AOA rarely exceeds 5 degrees.

To implement this restriction the following program can be used: in the atmosphere, pitch is determined by some (small) angle of attack, and then the linear control is used (see above). Notably, similar program is used in real life for lower stages of Soyuz launchers.

In the simplest case, AOA is assumed equal to zero. Then, to obtain the desirable trajectory, some small initial deviation from the vertical is necessary for a vertical-launched rocket.

Therefore, in addition to piecewise-linear control parameters (described above), we have to provide the duration of the atmospheric phase t_atm and the value of initial deviation Da. For the most rockets, the atmospheric phase can be approximated by the interval between start and the first stage separation. There is a certain reason in that: on the one hand, at the first stage separation the altitude is usually large enough. On the other hand, at the separation the AOA should be strictly controlled.

It is possible to implement more complex (then zero) AOA program for the atmospheric phase. To do that, reprogram column “Control (AOA)/a ”” of ”Control” worksheet.

Aerodynamic model (drag)

Physical model that accounts for the drag force leads to more complex pitch program. As far as I know, this program can not be expressed in the closed form. However, it can be computed by resolving (numerically) a system of ordinary differential equations. For more information, see: ”Optimal Control for Orbital Launcher”.

On each control interval, such program is determined by two free parameters: initial pitch value q(t_i) and some (adjoined) parameter F_h(t_i). Selection of the free parameters requires considerable accuracy: small changes in parameters may change system’s behavior significantly (up to the emergence of instability).

Aerodynamic model (drag + lift)

This model differs from the previous by accounting not only for a drag but rather for the full aerodynamic force. Despite larger complexity of the adjoined system equations, the usage of this model is very similar to the previous one. As a rule, the result is quite similar as well. When selecting the free parameters, the stability of the system is somewhat lower compared to the previous.

Restrictions

Whatever the control program is, it should satisfy the restrictions that are imposed by rocket’s design, launchpad construction, etc. “Restriction” section of the spreadsheet specifies some of such limitations.

Launch position

Most of the rockets are launched from a vertical position. Moreover, due to the design of the launchpad, vertical position should be maintained for the first several seconds of the flight. “Launch position” field specifies rocket’s initial position in degrees (vertical position corresponds to 90 degrees).

Clearing tower (sec)

“Clearing tower” field determine how long after the launch the rocket must remain in the specified position.

Max turn (deg/sec)

The angular speed of rocket turn can not exceed a certain limit. “Max turn” field determines such maximal angular speed

q - c

For most of the rockets the thrust must be directed precisely along the rocket’s axis – otherwise the rocket will spin. This field enforces the fixed angle (for example, zero) between the thrust vector and the aerodynamic axis of the vehicle. Naturally, this restriction makes sense only for the control that accounts for the lift force.

Q-Alpha

Aerodynamic structural load depends not only on dynamic pressure but also on the angle of attack. Because, in the first order of approximation, the load grows proportionately to the dynamic pressure, and lateral load grows proportionately to the AOA, restricting the maximum of their product is often used as a structural limitation.

On free parameters selection

Free parameters

As was shown above, for each control interval, the optimal (for the given physical model) program is determined by two free parameters.

Initial and final value of the pitch angle can be taken as the free parameters. Here we should not be distracted by the fact that initially rocket is in strictly vertical position – theoretically, nobody prevents us from changing rocket’s position immediately after the launch (as often happens in reality).

The number of the free parameters immediately follows from imposed boundary values. Namely: from the control point of view, we are interested in three terminal system parameters – vertical velocity, horizontal velocity and altitude (as we aim at orbital insertion rather then at particular coordinates – we are not interested in distance). The initial state of the system is known. Also, we impose an optimality restriction on the trajectory (maximal terminal horizontal velocity). After that, there are only two undetermined border conditions left: terminal altitude and terminal vertical velocity.

Therefore, we should find such control parameters that deliver given altitude and vertical velocity at the end of the trajectory. By construction of the optimal trajectory, horizontal velocity will be then maximal (naturally, only under the assumptions of the chosen physical model).

Strictly speaking, as Maximum Principle is only a necessary condition of optimality, the horizontal velocity does not necessarily have to be maximal or even extremal. However, provided that the input data is reasonable, it usually is.

If using n control intervals, we need to determine n+1 free parameters (2n if we allow discontinuity of the control). Because in the most cases it is sufficient to use only one interval, we will consider only this case.

Parameters of the various control models

Selection of the parameters is the easiest for the linear program. Initial and final values of the pitch angle are defined explicitly; the calculation of the control is trivial. Besides, the system’s behavior is stable to the small change of the parameters.

For the aerodynamic models, selection of the parameters is more complicated. First of all, the final value of the pitch angle can not be defined explicitly. Instead, some (adjoined) parameter has to be specified which determines the behavior of the adjoined system, and, ultimately, the control function. Secondly, the system is not very stable to the small changes of the parameters. They should be modified very carefully or the system’s behavior becomes unpredictable.

Combined program “AOA+linear” represents a special case. Effectively, it uses two control intervals: atmospheric (control by AOA) and vacuum (linear control). Implemented program of AOA control has one free parameter (value of the initial deviation). Linear control interval has, as usual, two free parameters. Therefore, for this model we must select three control parameters.

In some cases, the duration of the atmospheric interval also can be considered a free parameter. Then the total number of the free parameters would be four.

Parameter selection technique

Obviously, the control parameters can be selected manually. Sometimes, indeed, it has to be done this way. But in most cases the manual labor can be avoided or significantly reduced. The methods described above use standard Solver add-in.

Let’s consider two cases:

- search for two control parameters

- search for more then two control parameters

1. Search for two control parameters

This case usually corresponds to the search for the control parameters on the single control interval. Such parameters can be, for example, initial and final values of the pitch angle for the single interval of the linear control. Or, for example, initial value of the pitch angle and the adjoined variable for a/d models.

In this case the parameters only have to satisfy the border conditions. Optimality of the trajectory (under the assumptions of the given control model) is ensured by the very form in which control is constructed. Therefore, we have to find the values of the two parameters which deliver given terminal altitude and vertical velocity (usually, zero).

One of the approaches to such search is to minimize some function that serves as a measure of deviation from the boundary conditions (so called penalty function). For example, such function can be defined as: f = DH²+DV_y², where DH and DV_y – deviations of terminal altitude and vertical speed. This method can be used in the following way:

1. Using values for H and V_y from the section “System parameters”, place the penalty function in some cell f

2. Use Solver as follows:

Set Target Cell: f

Equal to: min

By Changing Cells: cells with unknown parameters

Subject to the Constraints: -

Default penalty function can be found in the “Control optimization” section.

2. Search for more then two control parameters

A search for more then two parameters may be necessary if more then one control interval is used. In this case satisfying the boundary conditions is not sufficient for the optimality. Two following methods can be used for the parameter search:

a) Direct optimization with restrictions

Use Solver in the following way:

Set Target Cell: V_x

Equal to: max

By Changing Cells: cells with unknown parameters

Subject to the Constraints: V_y=0, H=H*

b) Penalty function method

1. Place a target function (that includes a penalty function) in some cell f. Target function can be defined as:

f = a(DH² + DV_y²) - V_x

(where a – some constant, that determines the strictness of boundary conditions)

2. Use Solver in the following way:

Set Target Cell: f

Equal to: min

By Changing Cells: cells with unknown parameters

Subject to the Constraints: -

Default target function can be found in the “Control optimization” section.

Appendix А – columns description

Simulation worksheet

Worksheet “Simulation” implements the dynamics of the system. Each row corresponds to a state of the system at some moment. Below is the brief description of the columns.

t Time since launch (in seconds and minutes)

Stage Number of the current stage (minimal)

Pitch Pitch angle. Determined by the current control.

Coordinates

Altitude Altitude

Distance Distance (horizontal) from the launchpad (not used)

Velocity

V_x Horizontal velocity (relative to the surface and air)

V_x (abs) Horizontal velocity (absolute, i.e. accounting for Earth rotation)

V_y Vertical velocity

V Full velocity (relative to the surface and air)

m Full mass

Thrust (N) Full thrust (in newtons)

a Acceleration (characteristic)

CV Characteristic velocity

Acceleration

g Current gravitational (free fall) acceleration

(without Earth rotation – it’s accounted for in centrifugal acceleration)

a_x Horizontal acceleration

a_y Vertical acceleration

a centr. Centrifugal acceleration (absolute V_x is used)

а coriol. Coriolis acceleration (absolute V_x is used)

Atmosphere

T (°C) Temperature

r Relative density (to the sea level)

aerodynamics

AOA Angle of attack

q Dynamic pressure

C_x A/d drag coefficient (in linked system)

C_y A/d lift coefficient (in linked system)

R_t Projection of a/d force (in linked system)

R_n Projection of a/d force (in linked system)

R_x Projection of a/d force (in main system)

R_y Projection of a/d force (in main system)

Throttling Engines throttling program (by stage)

Thrust (kgf) Engines thrust (by stage)

Dry mass Current dry mass (including pressurization gas)

Fuel mass Current fuel mass (by stage)

Appendix B – FAQ

1. Spreadsheet recalculation is very slow

In Excel 2000 (and earlier versions) there exists a problem of so-called forward cross-worksheet references. In spreadsheets with large amount of cross-worksheet references this problem may lead to dramatic recalculation slowdown. If this problem appears it is recommended to use a special version: LaunchModel 2000.

2. Simulation ends at 600^th step/second. How to increase the number of steps ?

All rows of the simulation (starting from the second) are identical (up to the relative references). Therefore, to increase the time of the simulation, just copy down the last line for as far as needed. This should be done for both worksheets “Simulation” and “Control”.

Besides, don’t forget to increase correspondingly data area for the chart in the “Main” worksheet.

3. Can I increase the precision by reducing the time step ?

You can change the time step in the cell Dt in the «Main» worksheet.

By default the time step equals one second. Then, for a typical rocket, the discretization error is about 10 m/s. This model is a rather crude estimate and does not claim such precision anyway. That’s why we can assume default step as small enough for our purpose.

In other words, you can reduce discretization error but the model will not provide such precision for different reasons.

4. Why Runge-Kutta methods are not used ?

Runge-Kutta methods, as well as other higher order methods, assume the continuity of the right side of the differential equation. In this case, functions of thrust and mass substantially discontinuous at the moment of stage separation. The error due to the discontinuity will be larger then the precision increase due to the higher order methods.

Besides (see above): the model does not provide such precision for the reasons that are not related to the discretization.

5. How to reach a certain orbit ?

You can solve one of the three problems:

a) to reach a maximal velocity in perigee (and, consequently, a maximal apogee altitude) when perigee altitude and payload mass are given

b) to find a maximal payload mass when apogee and perigee altitudes are given

c) to build a trajectory when perigee, apogee and payload mass are given

- The problem (a) is solved automatically (for a given control). It is sufficient to find a control that satisfies the boundary conditions (see above: “Control” and, in particular: “On free parameters selection”)

- The problem (b) is solved by the search: we change the payload mass and for each value solve the problem (a).

- Alternatively to solve the problem (b), one can build a target function that will maximize the payload mass while minimizing deviation from the specified orbit. Then the problem is solved by minimizing the target function through variation of both control parameters and the payload mass.

- The problem (c) can also be solved either by search or by direct target function optimization: in this case we vary the time of engines cutoff (cell t in section “System parameters”).

Note that any of these problems can be solved by a direct minimization of the appropriate target function using Solver. See “Parameter selection technique” section above.