The first counterexample to the rigidity conjecture is the flexible connelly sphere, which is a non-convex polyhedron that may be "flexed". Connelly constructed the first embedded polyhedral surface that flexes by combining 4 parts together: a bottom part, a top part, and two crinkles.
The bottom part of the embedded polyhedral surface is obtained by deleting c and the 4 rods incident to c of the flexible octahedron in fig. 3, and each triangle is replaced with an upsidedown bottomless tetrahedron (a pit). Similarly, the top is obtained by deleting c' and the 4 rods incident to c of the flexible octahedron, and each triangle is replaced with a bottomless tetrahedron (a mountain). If the two aforementioned parts are glued together along their common
boundary, we get a polyhedral surface that flexes, as in fig. 6c.
 |
fig. 6a - The interior of the Flexible Connelly Sphere. The two parts of the bricard's octahedron can be seen easily. |
 |
fig. 6b - The exterior of the Flexible Connelly Sphere. |
 |
fig. 6c - The finished Flexible Connelly Sphere after taping the top and bottom pieces together. |
 |
fig. 6d - One of the two self-intersections. |
Unfortunately, this
surface has two self-intersections s and s' which corresponds to the crossing points of fig. 3 (as shown in fig. 6d). One
simple way is to cut out a small quadrilateral hole ghfh' at both
s and s', however this would create two holes on the
surface and the surface is not a closed polyhedron anymore. Therefore
a "mechanism" that possess the following properties is required to
close the polyhedral surface:
- Remove self-intersection.
- Cover the cutout surface during flexing of the ridge (a distance of gf along the valley.)
The Crinkle
 |
 |
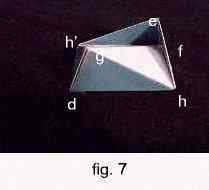This is where the crinkles are used to remove
the self-intersections. The crinkle is a simple mechanism that is also
based on the Bicard flexible octahedra. Start with 4 isoceles triangles ehf, eh'f, dhg, dh'g, then connect those 4 triangles to the quadrilateral cutout mentioned above as per fig. 7. Then we can say that the frameworks h(defg> andh'(defg) flex in conjunction because the crinkle is symmetric along dgfe, therefore dgef always remains coplanar regardless of the locations of h and h'. If we form a line through the midpoints of diagonals ge and df, the line is perpendicular to the diagonals. Realizing the fact that this line always perpendicular to the the midpoint of diagonal hh', according to the aforementioned lemma, we can say that the distance between of de is always equal to the length of diagonal gf. Therefore the crinkles (one at each intersection) can always cover the holes created by the cutout. This completes the counterexample to the rigidity conjecture because this closed polyhedral surfaface flexes without any self intersection.
The above example was then simplified to a polyhedral surface of total of 11 vertices and 18 faces by Kuiper and Deligne. The next section will present the simplest known flexible polyhedron with only 9 verticies.
PREV: Bricard's Flexible Octahedron
NEXT: Steffen's Simplest Known Flexible Polyhedron
Illustrated by Jonathan Shum
Center for Intelligent Machines
McGill University, Montreal, Canada.