Construction of Flexible Polyhedra

Bricard's flexible octahedra

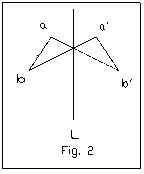LEMMA. Let aba'b' be a 4-gon with equal opposite sides ab=a'b', a'b=ab'. (Assume a,b,a',b' are not all in one line.) Then there is a unique line L meeting the diagonals aa', bb' intheir centers such that rotation by 180� about L leaves the 4-gon invariant by interchanging a with a' and b with b'.

Proof. If the diagonals aa' and bb' coincide, then aba'b' is a parallelogram. And L must be the line through this common midpoint perpendicular to the plane of the 4-gon aba'b'. On the other hand, if the midpoints x,y of aa' and bb' are distinct. Then the line L=xy needs to be perpendicular to both aa' and bb' because only a 180� rotation about L will interchange a with a' and b with b'. This is because aya' is an isoceles triangle with xy the median to the base. So xy is perpendicular to aa'. Similarly L is also perpendicular to bb'. This completes the proof.

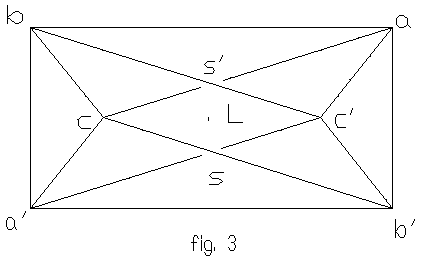
Now we can use the above lemma to construct the flexible octahedra by Bricard. Start with a 4-gon aba'b' with opposite sides equal, if we join a point c which is not on the line of symmetry to each vertex of the 4-gon, such "pyramid" will flex in E� (as long as c does not lie outside of the parallelogram if aba'b' coplanar because the edges will intersect.) Flex the "pyramid" and rotate 180� about L, then we can locate c' at exactly the same position as c before rotation. Finally joining c' to each vertices of the 4-gon will yield a flexible octahedron.

The example below showed a planar 4-gon aba'b' with rotation axis L perpendicular to the plane, note that this flexible octahedra will flex if we fixed ba' and twist a into and b' out of the plane but not to the other direction because of the bad intersections of the edges.

The flexible octahedron in figure 3 cannot be made with surfaces (due to its self-intersecting nature), but the framework is easy to build with straws and strings as in figure 4. See the flexible octahedra in motion in fig. 5. Click here for clearer images of the Flexible Octahedron

	fig. 4 Bricard's flexible octahedron made with straws and strings.
	fig. 5 Bricard's Flexible Octaheron In Motion

PREV: Rigidity Theories
NEXT: Flexible Connelly Sphere

Illustrated by Jonathan Shum
Center for Intelligent Machines
McGill University, Montreal, Canada.