Displaying 4-dimensional Structures

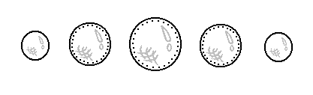
In the very first section of the material, we were made familiar with the hypersphere as it exists in the form of 3-dimensional slices. These slices are displayed once again here on the right below. In the section after that section (the previous section) we were introduced to what can be considered to be a 'working model' of a 4-dimensional plane. The goal of this section is to bring these 2 concepts together. As we learned in the previous section, our best conception of the fourth dimension exists in the form of the concept of multiple instances of our own 3-dimensional plane. Consider, for the sake of study, the '3-dimensional plane' spoken of here to exist in the form of the room that you are probably occupying right now. Because an array of 3-dimensional planes extends perpendicular to the third dimension (and hence outside of it), an array of 3-dimensional planes is what we will consider to be a 4-dimensional occurrence. Because we live in a 3-dimensional world, however, comprehending a '4-dimensional occurrence' can be difficult. Given the limitations we are under right now, we cannot approach an array of 3-dimensional planes as it exists as a 4-dimensional occurrence. Rather, our means of conceiving of an array of 3-dimensional planes exists in the form of what was introduced in the previous section as a "compressed" array of 3-dimensional planes. A "compressed" array of 3-dimensional planes, take note, is not a physical structure, but is rather a mental concept invented for our use as a way to envision the dimension above our own. It consists of the concept of what could be best described as multiple 3-dimensional planes occupying the space that we perceive our own 3-dimensional plane to take up.

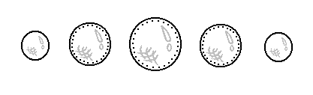Where, though, you may ask, do the actual planes themselves lie (given that it's not logically possible for multiple planes to occupy the space of a single plane)? The planes that we are assuming to occupy the 'same space' as our own plane, are in reality components of a 4-dimensional occurrence: they are separate from our plane by means of extension into the fourth dimension - separate by means of extension into directions that we, given our current knowledge, cannot comprehend! The assumption that these planes all occupy the 'same space' as our own 3-dimensional plane, you see, is the best possible conclusion that we can come to as of our own dimension, concerning the location of these planes in relation to our own 3-dimensional plane. (This is why, in the sequence shown in the previous section, the planes surrounding the creature's plane were moved onto the creature's plane: the best conclusion that the creature could come to concerning the location of these planes was that they occupied the 'same space' as his own plane). There exists a point later in the material, however, in which we document in detail the 4-dimensional directions that give each plane a distinct '4-dimensional separateness' from every other plane in the array. This future section, in showing us these directions, will allow us to think of an array of 3-dimensional planes from a 4-dimensional point of view, and will give insight as to how thinking in terms of a "compressed" array of 3-dimensional planes would relate to this 4-dimensional viewpoint. Because our concept, at the present moment, concerning the location of planes surrounding our own, is limited to how the planes are portrayed in their "compressed" state, we are to rely upon how they exist in this arrangement (that they occupy the 'same space' as our own plane) as our "best guess" as to where the planes actually lie. We have yet to arrive, however, at the section where we will be able to go beyond the limitations we are under right now, as stated - and in doing so expose these directions that we "can't comprehend" for what they truly are.

A hypersphere is considered to be a 4-dimensional object, for the very reason that it requires multiple 3-dimensional planes to be constructed. Because a 4-dimensional object is spread out across multiple 3-dimensional planes, in turn, a 3-dimensional 'slice' of the object ends up on each plane (as is the case with the hypersphere). In this sense a 4-dimensional object could be thought of as being an array of 3-dimensional objects. Being a step closer toward understanding how we would portray a hypersphere, we will now attempt to visualize what represents how we would directly experience a hypersphere: the 'compressed hypersphere'. What is the 'compressed hypersphere'? The 'compressed hypersphere' is the result of an attempt to contain an object of the fourth dimension - the hypersphere - within the third dimension. The first step involved in visualizing the 'compressed hypersphere' is to imagine that each and every slice of the hypersphere (as displayed above on the right) is itself assigned to its own 3-dimensional plane, each 3-dimensional plane being spatially separate, lined up side by side. The next step is to imagine, as we've done before, these multiple 3-dimensional planes to occupy the space that we perceive our own 3-dimensional plane to take up. As a result, the slices of the hypersphere end up occupying the same space as the 3-dimensional planes to which they were originally assigned. In effect, several 3-dimensional planes worth of slices are contained within the limits of our own 3-dimensional plane. The result is the 'compressed hypersphere' - the hypersphere "compressed" within the boundaries of the third dimension. Because we have "compressed" several 3-dimensional planes worth of slices onto a single 3-dimensional plane (the 3-dimensional plane that we happen to occupy), the slices end up "overlapping" on the plane onto which they were "compressed".

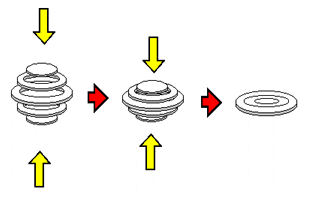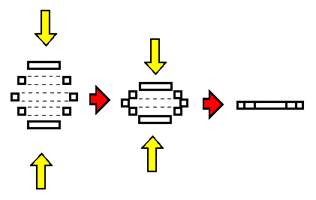
The fact that all of the slices now occupy the same space (that they "overlap") is a sort of "side effect" involved in containing the 4-dimensional hypersphere within the third dimension. In order to better understand the nature of how this "side effect" and the process of "compressing" structures are related, view to the right the formation of the 'compressed circle' and the 'compressed sphere'. The 'compressed circle' (shown in the illustration on top to the right) is the result of containing the 2-dimensional circle within the first dimension: as you can see, slices that began spread across several 1-dimensional planes end up on but a single 1-dimensional plane. The 'compressed sphere' (shown in the bottom illustration to the right) is the result of containing the 3-dimensional sphere within the second dimension: as you can see, slices that began spread across several 2-dimensional planes end up on but a single 2-dimensional plane. Upon viewing these two illustrations, one can quite clearly see that once put in a "compressed" state, the slices in these examples "overlap" in the same fashion as do the slices of the 'compressed hypersphere'. There is a means by which we can deal with the complications that the "overlapping" of the slices of the 'compressed hypersphere' brings, however: we are to "mentally designate" a unique fourth spatial coordinate to each individual slice found within the 'compressed hypersphere' - a coordinate standing for the 3-dimensional plane the slice was on before the hypersphere was "compressed". What this means is that each individual slice of the 'compressed hypersphere' is linked to a corresponding off-plane slice that lies on its own separate, unique plane. This concept can be observed upon examining how the "overlapping" slices in the illustrations of the 'compressed circle' and the 'compressed sphere' to the right relate to the positions they occupied before being "compressed". The 'compressed hypersphere' - the result of containing several 3-dimensional planes worth of the slices of the hypersphere onto our own 3-dimensional plane - represents our basic conception of how we would experience being in the actual presence of a hypersphere. What, however, if our purpose was not to 'directly experience' the hypersphere, but rather to study its slices in detail?

A stack-diagram is used to study up close the slices of structures that extend into the next dimension. The hypersphere is such a structure. This method of portraying structures is notably different from the approach just described: rather than relating the structure to the plane we physically occupy, this method involves constructing a diagram as the means of portraying the structure. We are to assume, as part of the process of becoming familiar with this concept, that the slices of a hypersphere are spread across a given array of 3-dimensional planes (the ends of which extend, as stated earlier, into the fourth dimension). Our goal, as of now, is to represent this hypersphere in stack-diagram form.

It is upon being introduced to each new dimension that there is provided a new pair of directions into which extension can occur. We will name these directions 'direction A' and 'direction B'. The planes of the previous dimension extend into these 2 opposite directions (as we witnessed in the sequence shown in the previous section), forming an array that is arranged in a distinct linear fashion. It is for this reason that a stack-diagram is therefore also linear, extending by its own nature into 2 opposite directions. To create a stack-diagram, we first line up horizontally in a row the slices of the structure being displayed, presenting them in the same linear fashion in which they are arranged in physical reality (as is done in the top illustration to the left). The next step is to associate the linear extension that occurs in the stack-diagram, with the extension into the next dimension that occurs in physical reality. We do this - as is done in the bottom illustration to the left - by labeling the diagram's directions of extension using the names of the actual directions that they represent: the directions that we identified above as 'direction A' and 'direction B'. The result, as you can see, is the hypersphere as we will be working with it: in stack-diagram form. In the next section we become more familiar with using a stack-diagram to portray structures.