MATRICES AUMENTADAS
Existe una forma fácil de representar sistemas de ecuaciones lineales, que nos permite efectuar el algoritmo de la eliminación gaussiana, trabajando sólo con los coeficientes sin necesidad de colocar las variables, por ejemplo:
Hay dos puntos que prestar atención en este arreglo. Las variables en todas las ecuaciones deben escribirse en un mismo orden, y deben quedar "alineadas", es decir, viendo el ejemplo anterior, 5x1 debe quedar debajo de 3x1, y asi sucesivamente.
Un arreglo rectangular de números se llama Matriz. La matriz (2) recibe el nombre de Matriz aumentada del sistema (1). Los Renglones (lineas horizontales) de la matriz aumentada contienen los coeficientes de la ecuación correspondiente junto con el término constante de dicha ecuación.
Ejemplo 1.- La matriz aumentada del sistema de ecuaciones lineales:
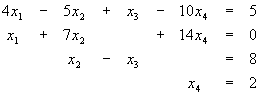 es
es 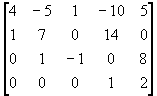
Ejemplo 2.- La matriz:
es la matriz aumentada del siguiente sistema de ecuaciones lineales:
Ejemplo 3.- Resolver el siguiente sistema de ecuaciones lineales mediante la técnica de eliminacion gaussiana

 su matriz aumentada es
su matriz aumentada es 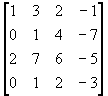
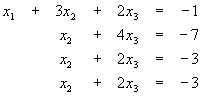
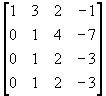
Puesto que la tercera y cuarta ecuación o renglón, se resta la tercera de la última ecuación o renglón y nos queda:
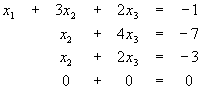
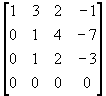
Ahora restamos la segunda ecuación o renglón de la tercera para eliminar la variable xx2 de esta última ecuación.
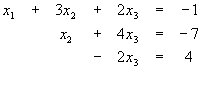
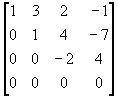
Ahora dividimos la última ecuación entre (-2) para simplificar la ecuación:
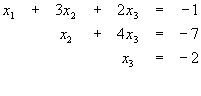
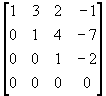
Puesto que x3 = -2 , mediante sustitución regresiva en la segunda ecuación x2 = 1, y sustituyendo estos valores en la primera ecuación determinamos que x1 = 0
RESPUESTA.- El conjunto solución es:
Ejercicios Resueltos y propuestos
|
|