The Soma Cube Puzzle

The Soma Cube Puzzle - 2

Shifting 7

A SOMA challenge: The number 7 piece can occupy 4 positions in the cube (not counting rotations and reflections). Construct the SOMA Cube with the 7 piece in each of the following positions:

Bury the 7

A SOMA Challenge: Construct the "Buried 7" solution of SOMA cube, shown at the right, where the number 7 piece is placed so that it's central cube is at the center of the SOMA cube. Only the three outward faces of its three arms are visible (shown in yellow). Of course, more than one solution may be possible.

The Balancing Soma Cube

This interesting information about the Soma Cube was published in Martin Gardner's Mathematical Games column in July, 1969.

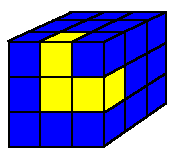
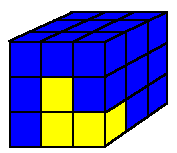
Martin Gardner notes in the article that there are 240 different ways the cube can be formed not counting rotations and reflections as being different. This figure was established in 1962 by John Conway and M.J.T. Guy, who were mathematicians at the University of Cambridge. In analyzing his work, Conway discovered the curious fact that only one of the 240 solutions allows the Soma cube to be balanced on a pedistal that touches only the central square of the cube's 3 by 3 unit base. This solution is diagrammed below. The central square of the bottom layer is the one that rests on the pedistal.

TOP

MIDDLE

BOTTOM

6	7	7
6	6	7
3	1	1

5	5	7
3	6	4
3	1	4

5	2	4
5	2	4
3	2	2

Addendum:
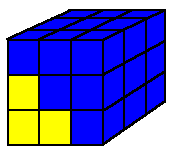
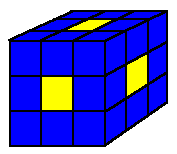
The following additional solution to the balancing cube has been produced by Stuart Collins of Nottingham, UK in June, 1998 and refutes Conway's uniqueness assertion stated above!

Are there more solutions to this problem? Mr. Collins conjectures that any of the flat 4-cube pieces ( 2,3, and 4 ) might serve as the balance piece. It only remains to be shown that the 3 piece can serve this function.

TOP

MIDDLE

BOTTOM

2	2	1
7	1	1
7	7	3

2	6	6
5	5	3
7	5	3

2	4	6
4	4	6
4	5	3

Piece Duplication

Doubling each dimension of any piece will multiply the volume by 8. For any of the pieces comprised of 4 unit cubes, this increases the volume from 4 cubic units to 32 cubic units. For piece number 1, the volume increases from 3 cubic units to 24 cubic units. This equals the total number of unit cubes in the remaining 6 pieces. This poses a possible problem: Can you construct a figure similar to the number 1 piece but with all dimensions doubled, using the remaining 6 Soma pieces? The answer is yes, and the challenge is to construct this figure.

Solutions for selected figures in the Soma Gallery

I am including a few illustrations of how to solve these figures. The viewer is urged to make every effort to solve these figures without consulting these solutions. They can all be done if you work at it for awhile. You certainly get more satisfaction if you discover the solution yourself. Then, once you solve it, you may wish to compare your solution with mine.

These figures have graphics showing the solutions:

The Castle
The Gallows
The Pyramid
The Scorpion
The Tunnel
The Church
The Bed

Two Set Figures

If you have two Soma sets, you can try some of the two set constructions. We have illustrations of the following two set figures:

Three Ways Out (Illustrated)

More Illustrations:
Memorial II
Up and Down
The Factory
The British Square
The Sentry Tower

Two Set Figure Solutions:

Three Ways Out

Gallery

Return to Home Page

This page hosted by Get your own Free Home Page

Hosted by www.Geocities.ws