
Calculating a River's Current

"Hey GM, how fast is the water moving?"
If you are the kind of GM that answers that question with, "as fast as I want it to move!" then this page is not for you. Stop wasting your time and turn around now. On the other hand, if you are the kind of GM that likes some realism in your game world, and you want the answer you give to that question to match what the players see on the map, then this page is for you.
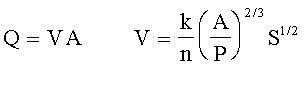
How do I use this?
That is known as Manning's Equation. There are at least two ways to apply it to achieve realism in your game world. First, it will let you estimate the current of a river or stream you see on one of your maps. Second, if you are drawing a map that includes a river or stream for which you have already decided a current, it will let you figure out how wide and deep to make it, and how much slope to depict with contour lines. Further down the page, we will also address converting currents to "movement points" as used in the rules of Pilot's Almanac.
Once you have figured out this technique you can also twist it around, working it backwards and sideways, to sort out a few other things as well. And, since we have the magic of Java and the web, it will be much less painful than all those wordy math problems you hated while in school!
The Links
To make this as easy as it is, we have to go off-site to scrounge some additional information and to open up some Java applications. Clicking on the buttons below should open up new windows that give you access to them. If you have a slow machine or connection, you may want to read through the rest of this page, then come back and open them once you are familiar with how we will use them.
Enough Talk! Let's Get Started!
Let's use Manning's Equation to estimate the current of the Ulmerien River at the village of Feryce. We will take our measurements just across from where the mill sits on its small island. (Click here:  to open up a map inset.)
to open up a map inset.)
 Start by using the link-button in the list above to open up the Manning's Equation site. Note that the selected button indicates we are working in feet and seconds. Even if you prefer working in metric, leave it here for this example. Now, under the heading "Select Calculation," click the uppermost button to choose "Velocity (V) and Discharge (Q)" then use your mouse and keyboard to clear out the default values in each block.
Start by using the link-button in the list above to open up the Manning's Equation site. Note that the selected button indicates we are working in feet and seconds. Even if you prefer working in metric, leave it here for this example. Now, under the heading "Select Calculation," click the uppermost button to choose "Velocity (V) and Discharge (Q)" then use your mouse and keyboard to clear out the default values in each block.
Now that we are ready to begin, take some measurements from the map to determine the area of the cross-section of the river. Here, with my CC2-MH version of the map, I measure a width of 260 feet from the beginning of the deep water on the north side all the way over to the bank on the south side. For depth, the map key indicates the river is at least 15 feet deep. As GM, you have to decide just how deep you want it to be, but for this example, let's say it is about 16 feet deep. Mulitplying the two figures together, we get a cross-section area of 4,160 feet, so we will enter 4160 into that block.
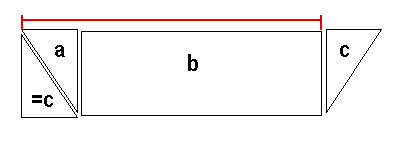 "Wait a minute!" I hear you say. "Why didn't you measure from one bank all the way to the other?" Since the banks here at Feryce are not straight up and down, that technique would result in an inaccurate measurement. To be perfectly accurate, I could calculate the area of the deep water, then add the triangular areas near the banks. But I also can just measure from the edge of the deep water on one side to the bank on the other and it will work out fairly close. If the banks are straight up and down, as they are in some places, then you should measure from one bank to the other.
"Wait a minute!" I hear you say. "Why didn't you measure from one bank all the way to the other?" Since the banks here at Feryce are not straight up and down, that technique would result in an inaccurate measurement. To be perfectly accurate, I could calculate the area of the deep water, then add the triangular areas near the banks. But I also can just measure from the edge of the deep water on one side to the bank on the other and it will work out fairly close. If the banks are straight up and down, as they are in some places, then you should measure from one bank to the other.
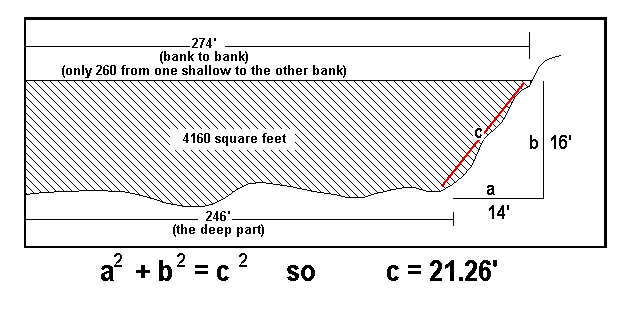
Next, calculate the "wetted perimeter" of the river. This is pretty much the width of the bottom (along the deep part), plus the length of the slope of each underwater bank (see the illustration at left). I use my rusty geometry to figure out the bank's length with a simple calculator -- from the map, I measure the shallow bit of water at each bank as about 14 feet wide; I've made the depth of the river 16 feet; so the length of each slope works out to about 21.26 feet.

We add up the length of the two slopes and the width of the river's bottom to get 288.52 feet, so we enter 288.52 into the block for "Wetted Perimeter."
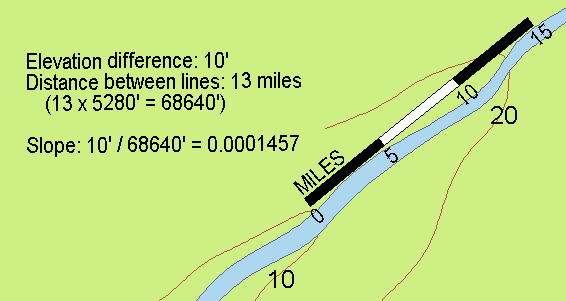
Next, determine the slope of the river's bottom. If working from a map that shows contours crossing the river, calculate the percentage of slope of the river bottom by measuring the contour interval (elevation difference represented by the contour lines) and dividing that figure by the distance between two adjacent contour lines that cross the stream (see illustration). Most of the time, however, you are going to find there is only one line crossing the stream, and maybe none, because the lines that would cross the stream are further apart than your map is wide. In that case, you can use the estimated values from the table below.
I calculated the average slope of the Ulmerien by determining the river's elevation as derived from the map of Geda (80 feet above sea level at the banks), then dividing by the length of the river between Geda and the sea. That works out to an average slope of 0.0001457 which is what I used for the slope of the river bottom at Feryce.
| Mountain Stream | 0.0075758 | 0.25 mile |
| Highland Stream | 0.0037879 | 0.5 mile |
| Highland River Valley (Noron) | 0.0011364 | 1.7 miles |
| Lowland River Valley (Olokand) | 0.0002841 | 6.7 miles |
| Flat Plains (Tashal - Dyrisa) | 0.0000947 | 20 miles |
| Coastal Reaches (Golotha) | 0.0000473 | 40 miles |
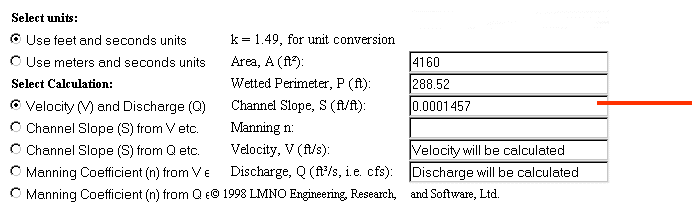
Once you've determined the slope of the bottom, plug it in here.
Nearly there! We have just one more number to look up. It is called "Manning's n" and is a measure of the turbulence and friction created by the condition of the river's bottom. Check the real-life examples (from the list of links above) or choose a value from the table below.
| Canal - clean & straight | 0.022 |
| Canal - gravelly | 0.025 |
| Canal - weedy | 0.03 |
| Canal - stones or cobbles | 0.035 |
| Natural - clean & straight | 0.03 |
| Natural | 0.033 |
| Natural - weedy | 0.04 |
| Natural - large stones | 0.065 |
| Major River | 0.035 |

The Ulmerien is a major river, so we will use that value (from the table above) and plug it in here.
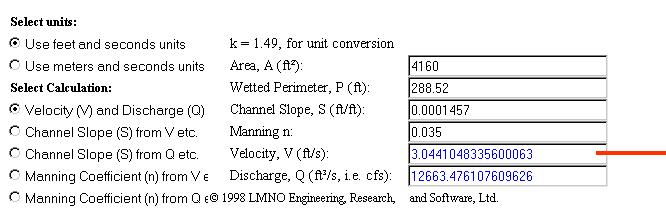 Now click on that button and let's see what we get! If you've used the same values I have, you should get a result that indicates a current of about 3.04 feet per second. Now, that number doesn't mean much to most of us, so use the button from the list of links (above) to get to an online site that will quickly convert that number into something more usable. I like working in metric for the rest of this, so I converted it to: 3.34 kilometers per hour.
Now click on that button and let's see what we get! If you've used the same values I have, you should get a result that indicates a current of about 3.04 feet per second. Now, that number doesn't mean much to most of us, so use the button from the list of links (above) to get to an online site that will quickly convert that number into something more usable. I like working in metric for the rest of this, so I converted it to: 3.34 kilometers per hour.
"How fast is that?" you ask. Well, a Hârnic talbar can be rowed at 4 kilometers per hour in smooth water. If the captain shouts and threatens, the crew can make that 6 kilometers per hour for a while. So, with a river current of 3.34 kilometers per hour, a rowing talbar would be able to make slow progress upriver in the area of Feryce.
Starting From Scratch
You have probably already noticed one shortcoming of using Manning's Equation: before you can use it, you have to know the dimensions of the watercourse as well as its slope. You can pull them from a map, as we did above, but where do you start if you are just now making the map?
Well, you could just invent them, drawing the river at whatever size looks nice. But true pedants (or grognards, if you prefer) will not be happy with that approach unless their invention ties into the rest of the world they are creating. One way to help that happen is to take a look at the catchment area of the river and the amount of precipitation it collects. You can easily measure the catchment area from the map. But, unless your world is much more developed than most, you will have to invent the amount of annual precipitation. Once you have those two facts, you can use a very simplified application of the Rational Formula to estimate the cross section of the watercourse. Nowadays, sophisticated computer models have replaced the rational formula in most applications, but it is still widely used for properly sizing drainage systems in urban area and will meet your needs pretty nicely.
As its name implies, the Rational Formula is a straight-forward approach that assumes most of the precipitation that falls within a catchment area makes its way to the watercourse and flows downstream. Some is lost to plant and animal life, some is absorbed into the soil, and some evaporates, but the rest makes it there and flows away, creating a watercourse of a certain dimension if all the precipitation is to be handled without flooding every time it rains. The percentage that makes it to the watercourse is handled by the dimensionless variable "C" in the formula which ranges in value between 0 and 1.0. If all the water makes it to the watercourse (the world is paved and nothing evaporates), then C = 1.0. If only half makes it, then C = 0.5, etc.
The value "A" is the area of the catchment, and "I" is the amount of precipitation it collects over a given time period. You can use any system of measure you like. I convert mine to depth and area measurments in feet and time periods in seconds so that I end up with a flow rate ("Q") expressed in cubic feet per second.
Let's take the Ulmerien as an example. My rough measurement gives the Ulmerien's catchment area as about 45 hexes, or about 3,897,000 acres, or about 169,753,320,000 square feet. If I assume an annual precipitation of 4 feet per year, and use a loss coefficient of 0.95, then we have:
Dividing by 31,104,000 (the number of seconds in a H�rnic year), I get a flow rate of 20,739 cubic feet per second at the mouth of the Ulmerien. Bear in mind that is the average flow rate - it will be higher at some times and lower at others.
But what do you do with that figure? Well, you have to go back to making some assumptions. First, what is the average current here at the mouth of the river? Let's make it only one foot per second (about one kilometer per hour, or 1 MP in game terms). That then means the cross section of the river has to be 20,739 square feet. If I had made the current two feet per second (about 2.2 kilometers per hour) then the cross section of the river would be half that, or about 10,370 square feet. But let's stick with the original figure of 20,739 square feet and a current of one foot per second.
And, finally we have to assume one of the dimensions - either the river's width, or its depth. Let's assume the river is 16 feet deep here at the mouth. That then makes its width about 1,296 feet, or about 395 meters, or about one quarter of a mile at the mouth.
What about some point upstream? What should the river look like at a spot, say, five leagues upstream from Geda?
My rough measuring says the catchment for the river up to that spot amounts to about nine hexes, or about 779,400 acres, or about 33,950,664,000 square feet. So, we have:
Dividing by 31,104,000 (the number of seconds in a H�rnic year), I get a flow rate of 4,366 cubic feet per second at the spot on the Ulmerien River I have named Jerembak. If we make the current here about 4.5 feet per second (about 5 kilometer per hour) then our cross section has to amount to 970 square feet. If we make the river about six feet deep here, then its width must be 162 feet, or about 50 meters, or about one quarter of a furlong.
That seems about right, because at Geda, the river is about 200 feet wide as I measure it on the map. How deep is the river at Geda? Well, we have a catchment area of about 12 hexes, or about 1,039,200 acres, or about 45,267,552,000 square feet. So, we have:
Dividing by 31,104,000 (the number of seconds in a H�rnic year), I get a flow rate of 5,822 cubic feet per second at Geda. If we assume a current of about 4 feet per second (about 4.4 kilometers per hour), then we have a cross section of about 1,456 square feet. At this spot, the Ulmerien is about 200 feet wide, but measured from one bank to the other shallow (see above), we get a width of about 175 feet. That then makes the depth of the Ulmerien at Geda about 8 feet and four inches (8.3 feet).
Now, take a look at the web page that runs Manning's Equation for you and you will note you can switch the calculation so that Q (flow rate) is your input and, if you have the dimension of the channel already, slope and velocity (current) will be calculated for you. By working back and forth, and making some reasonable assumptions in the absence of facts, you can pretty much sort out your river. If you get stuck, remind yourself it is just a game and recall the words of Aristotle:
It is the mark of an educated person to look for precision in each class of things just so far as the nature of the subject admits.
Movement Points
According to the rules offered in Pilot's Almanac, a "reasonably navigable" river has a current of between one and three movement points (MP), with faster rivers having currents of between four and six movement points. I have deduced that one MP, as used in the rules concerning river currents and oar-propelled vessels, is equal to about one kilometer per hour. A talbar that is "pressing the oarsmen" has a movement rate of six kilometers per hour, so in light winds is capable of moving upstream in all but the fastest currents under oar power alone. Anything over about five kilometers per hour, however, is not really navigable unless some sort of cable pull is used to move vessels upstream.
That said, you now have all the information you need to calculate the current of the rivers on your maps, and to assign them a movement point value based on the ratio of one MP for each kilometer per hour of the river's current.


This page hosted by
 Get your very own!
Get your very own!