Main: The Wave equation

The three dimensional problem

The three dimensional wave equation problem is

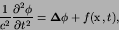$\begin{displaymath} {1\over c^{2}}{{\partial^2 \phi}\over{\partial {t}^2}} = {\hbox{\boldmath$\Delta$}}\phi + f({\hbox{\boldmath$x$}},t), \end{displaymath}$

(39)

together with a radiation condition. Specifically, waves should travel outwards from points where 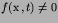$f({\hbox{\boldmath$x$}},t)\neq 0$ towards infinity rather than travel in from infinity.

The associated Green's function, 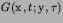$G({\hbox{\boldmath$x$}},t;{\hbox{\boldmath$y$}},\tau)$ satisfies

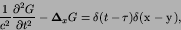$\begin{displaymath} {1\over c^{2} }{{\partial^2 G}\over{\partial {t}^2}}-{\hbox... ...ta(t-\tau)\delta({\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}), \end{displaymath}$

(40)

together with the radiation condition that disturbances should radiate away from the point of disturbance, 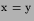${\hbox{\boldmath$x$}}={\hbox{\boldmath$y$}}$ , rather than towards it.

For the usual reasons, it follows that the solution of (8.1) is

$\begin{displaymath} \phi({\hbox{\boldmath $x$}},t) = \int_{-\infty}^{\infty}\ke... ...ath $y$}},\tau) \,d^{3}{\hbox{\boldmath $y$}}\kern 4pt d\tau. \end{displaymath}$

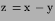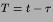If we introduce ${\hbox{\boldmath$z$}} = {\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}$ and $T=t-\tau$ then (8.2) becomes

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}}-{\hbox{... ...math $\Delta$}}_{z}G = \delta(T)\delta({\hbox{\boldmath $z$}}) \end{displaymath}$

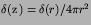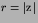Since $\delta({\hbox{\boldmath$z$}})=\delta(r)/4\pi r^{2}$ , where $r=\left\vert{\hbox{\boldmath$z$}}\right\vert$ it follows that G=G(r,T). Thus

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}}-{1\over... ...{\partial {r}^2}}(rG)={1\over 4\pi r^{2}}\delta(T)\delta(r), \end{displaymath}$

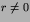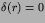For $r\neq 0$ we have $\delta(r)=0$ , hence after multiplying through by r

$\begin{displaymath} \left({1\over c^{2}}{{\partial^2 }\over{\partial {T}^2}} - {{\partial^2 }\over{\partial {r}^2}}\right)(rG) = 0 \end{displaymath}$

which is the one-dimensional wave equation for rG(r,T). Using the D'Alembert solution for the one-dimensional wave equation we conclude that

$\begin{displaymath} G(r,T) = {F(T-r/c)\over 4\pi r} + {E(T+r/c)\over 4\pi r} \end{displaymath}$

for some functions F(T-r/c) and E(T+r/c). (The factor of 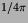$1/4\pi$ is introduced purely for convenience in what follows.)

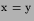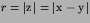The radiation condition that disturbances should radiate away from ${\hbox{\boldmath$x$}}={\hbox{\boldmath$y$}}$ rather than towards it becomes the condition that disturbances should move away from r=0 ( $r=\left\vert{\hbox{\boldmath$z$}}\right\vert=\left\vert{\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}\right\vert$ ) rather than towards r=0. Since F(T-r/c) represents a wave moving away from r=0 and E(T+r/c) represents a wave moving towards r=0, it follows that we must take

$\begin{displaymath} G(r,T) = {F(T-r/c)\over 4\pi r}. \end{displaymath}$

This solution is singular as $r\to 0$ , so we define a ``generalised version'' of it by

$\begin{displaymath} G(r,T) = \lim_{\epsilon\to 0} \left( H(r-\epsilon){F(T-r/c)\over 4\pi r}\right) \end{displaymath}$

where the point r=0 is excluded, and use the result from section 5.4 that

$\begin{displaymath} {\hbox{\boldmath $\Delta$}}_{z}€\left[ \lim_{\epsilon\to 0}... ...= {f''(r)\over 4\pi r} - f(0)\delta({\hbox{\boldmath $z$}}). \end{displaymath}$

This shows that

$\begin{displaymath} {\hbox{\boldmath $\Delta$}}_{z}G = {F''(T-r/c)\over 4c^{2}\pi r} - F(T)\delta({\hbox{\boldmath $z$}}) \end{displaymath}$

and, differentiating G twice with respect to T we obtain

$\begin{displaymath} {{\partial^2 G}\over{\partial {T}^2}} = {F''(T-r/c)\over 4\pi r} \end{displaymath}$

so that

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}} - {\hbo... ...{\boldmath $z$}}) = \delta(T)\delta({\hbox{\boldmath $z$}}). \end{displaymath}$

Thus

$\begin{displaymath} F(T) = \delta(T) \end{displaymath}$

and therefore

$\begin{displaymath} G(r,T) = {\delta(T-r/c)\over 4\pi r}. \end{displaymath}$

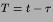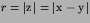Recalling that $T=t-\tau$ , $r=\left\vert{\hbox{\boldmath$z$}}\right\vert=\left\vert{\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}\right\vert$ ,

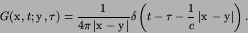$\begin{displaymath} G({\hbox{\boldmath$x$}},t; {\hbox{\boldmath$y$}},\tau) = {1... ...{\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}\right\vert\right). \end{displaymath}$

(41)

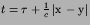Note that G=0 except where $t=\tau+ {1\over c}\left\vert{\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}\right\vert$ .

An important point:

The delta function in the Green's function (8.3),

$\begin{displaymath} G({\hbox{\boldmath$x$}},t; {\hbox{\boldmath$y$}},\tau) = {1... ...{\hbox{\boldmath$x$}}-{\hbox{\boldmath$y$}}\right\vert\right). \end{displaymath}$

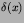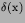is a scalar delta function not a vector delta function. That is, it is a one dimensional delta function $\delta(x)$ rather than a three dimensional delta function $\delta({\hbox{\boldmath$x$}})$ .

Main: The Wave equation

Hosted by www.Geocities.ws