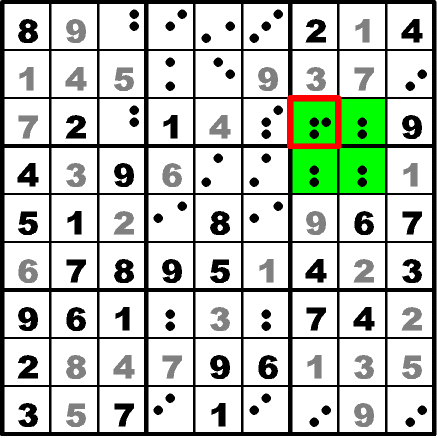
On April 9 2006, I was enjoying a cup of coffee and participating in my favorite Sunday morning ritual; solving the daily Sudoku puzzle from the local newspaper! As usual I got stuck, so the next thing to do was to fill the rest of the grid with dots:

I was still stumped, until I noticed a strange pattern on the 4 colored (green) squares. All 4 squares have candidates 5 or 8; except for the (red) highlighted square, which also has candidate 6 to boot.
Then it dawned on me... if the (red) highlighted square was not 6, then the 4 colored (green) squares would have two answers...
| either: | or: | |||
| 5 | 8 | 8 | 5 | |
| 8 | 5 | 5 | 8 | |
OH-NO! Even if the other 77 (out of 81) squares were filled out, there is no way they could influence the 4 remaining squares to become either one answer or the other. Which brings us to the most sacred of Sudoku rules: "Every Sudoku puzzle has a unique solution". Because of the sacred rule, then the highlighted square has to be 6, in order for the puzzle to have a single solution.
I'm calling this method (though it's occurence is extremely rare) the HIGHLANDER; as "There could BE only ONE".
However, using this method could be dangerous. It assumes that the particular Sudoku you are working on has been thoroughly checked out to assure that there can be only one solution. If you are working with a puzzle designed by Michael Mepham or Will Shortz, then you're OK. Then again if you're relaxing in the park filling out a Penny Press book... beware!