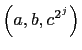 is a solution to a primitive
Pythagorean triangle, where
is a solution to a primitive
Pythagorean triangle, where This section in pdf form triples3.pdf
It is well-known that if ![]() is a solution to a
Pythagorean triangle, where
is a solution to a
Pythagorean triangle, where ![]() is the hypotenuse, then the
Mersenne prime
is the hypotenuse, then the
Mersenne prime ![]() divides
divides ![]() , and the Fermat prime
, and the Fermat prime ![]() divides
divides
![]() . In this section, I show that if
. In this section, I show that if
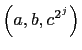 is a solution to a primitive
Pythagorean triangle, where
is a solution to a primitive
Pythagorean triangle, where ![]() is a non-negative integer, then
every Mersenne prime less than or equal to
is a non-negative integer, then
every Mersenne prime less than or equal to
![]() divides
divides ![]() , and every Fermat prime less
than or equal to
, and every Fermat prime less
than or equal to
![]() divides
divides ![]() .
.
If ![]() is a solution to the Pythagorean triangle
is a solution to the Pythagorean triangle
![]() then
then ![]() is a Pythagorean triple. If,
additionally,
is a Pythagorean triple. If,
additionally, ![]() , and
, and ![]() are pairwise relatively prime then
are pairwise relatively prime then
![]() is a primitive Pythagorean triple (PPT), and
is a primitive Pythagorean triple (PPT), and
![]() is a Primitive Pythagorean triangle.
is a Primitive Pythagorean triangle.
All PPT's are given by the parametric equations
When computing the PPT
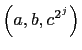 , it is
convenient to express
, it is
convenient to express ![]() , and
, and ![]() in terms of Gaussian
integers
in terms of Gaussian
integers
![]() . To do so, let
. To do so, let ![]() where
where ![]() and
and ![]() are relatively prime, positive integers having opposite parity.
Let
are relatively prime, positive integers having opposite parity.
Let ![]() and
and
![]() . And let
. And let ![]() be a non-negative
integer. Then there exists positive integers
be a non-negative
integer. Then there exists positive integers ![]() and
and ![]() such that
such that
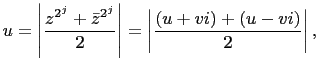 and
and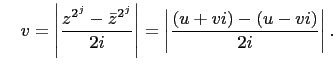
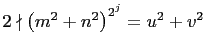 . Hence
. Hence
Thus, all primitive Pythagorean triples of the form
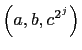 are given by the parametric equations
are given by the parametric equations
Then
If
![]() and
and ![]() are positive integers such that
are positive integers such that
![]() is a primitive Pythagorean triangle, and if
is a primitive Pythagorean triangle, and if ![]() divides
divides ![]() then we are
going to show the following:
then we are
going to show the following:
Previously, it was shown (here), that those three
items are true for the case ![]()
I will, first, state and prove a theorem on the divisors of ![]() ,
and of
,
and of ![]() , where
, where
![]() is a PPT. Then the case
where
is a PPT. Then the case
where ![]() will be proven in the corollary. If
will be proven in the corollary. If ![]() in
equation (19) then
in
equation (19) then
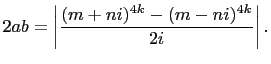
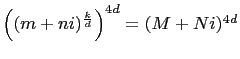 for some
for some
Which implies
Similarly,
Which implies
Therefore
![]() where
where
![]() and
and
![]() . Which implies
. Which implies
Similarly
Then, if
Therefore
Let
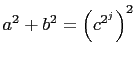 be a primitive Pythagorean
triangle where
be a primitive Pythagorean
triangle where ![]() is a nonnegative integer. Let
is a nonnegative integer. Let ![]() be any
Mersenne prime less than or equal to
be any
Mersenne prime less than or equal to ![]() . And, let
. And, let ![]() be
any Fermat prime less than or equal to
be
any Fermat prime less than or equal to ![]() . Then
. Then
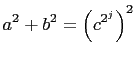
is a primitive Pythagorean triangle where
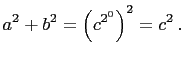
So there exists integers
![$\displaystyle \left(c^{2^{j+1}}\right)^2=\left[\left(c^{2^j}\right)^2\right]^2
=\left(a^2+b^2\right)^2
=\left(a^2-b^2\right)^2+(2ab)^2$](img351.gif)
. Let