


Next: Primitive Pythagorean triangles where
Up: Primitive Pythagorean triangles where
Previous: Primitive Pythagorean triangles where
Contents
From Table (1), let
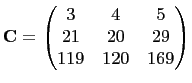
and
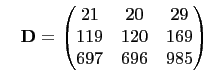
So, solving for
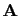 in the matrix equation
in the matrix equation
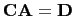 , we find that
, we find that
Let
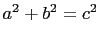 . Then
. Then
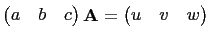 where
where
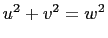 , and
, and 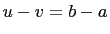 . Furthermore,
. Furthermore,
where 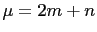 and
and 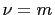 . Therefore, if
. Therefore, if 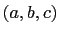 is a
primitive Pythagorean triple then so is
is a
primitive Pythagorean triple then so is 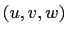 . Thus, if
. Thus, if
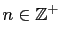 , then
, then
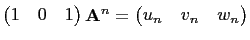 gives the
gives the 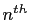 primitive Pythagorean triple such that
primitive Pythagorean triple such that
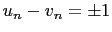 .
.
We have, using matrix
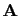 , if
, if 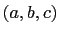 is a primitive
Pythagorean triple then
is a primitive
Pythagorean triple then
where 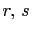 and
and 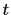 are pairwise relatively prime,
are pairwise relatively prime,
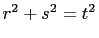 , and
, and
Also, 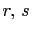 , and
, and 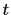 are positive integers, since
are positive integers, since 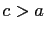 . Hence
. Hence
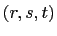 is a primitive Pythagorean triple.
is a primitive Pythagorean triple.
Similarly, if 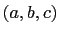 is a primitive Pythagorean triple then
is a primitive Pythagorean triple then
where 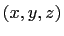 is a primitive Pythagorean triple such that
is a primitive Pythagorean triple such that
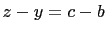 .
.
Let
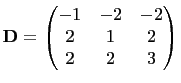
and
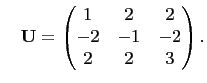
Joe Roberts2 has shown that
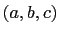 is a Primitive Pythagorean triple if and only if
is a Primitive Pythagorean triple if and only if
where
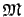 is a finite product of the matrices
is a finite product of the matrices
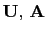 , and
, and
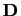 .
.



Next: Primitive Pythagorean triangles where
Up: Primitive Pythagorean triangles where
Previous: Primitive Pythagorean triangles where
Contents
f. barnes
2008-04-29
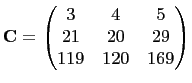 and
and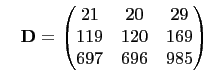
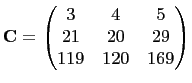 and
and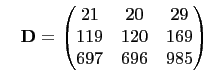
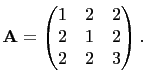
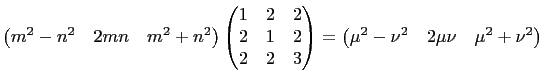
![]() , if
, if ![]() is a primitive
Pythagorean triple then
is a primitive
Pythagorean triple then
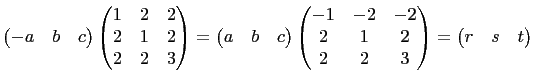
![]() is a primitive Pythagorean triple then
is a primitive Pythagorean triple then
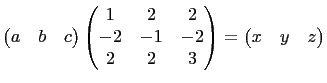
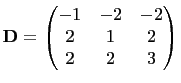 and
and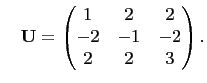
![]() is a Primitive Pythagorean triple if and only if
is a Primitive Pythagorean triple if and only if