A perfect number is a positive integer that is equal to the sum of
its divisors excluding itself. For example ![]() is a perfect number
since its divisors are
is a perfect number
since its divisors are ![]() and
and ![]() where
where ![]() All
even perfect numbers are of the form
All
even perfect numbers are of the form
![]() where
where ![]() is a prime. Such primes are called Mersenne primes.
The first five perfect numbers are
is a prime. Such primes are called Mersenne primes.
The first five perfect numbers are
It's not known if there are any odd perfect numbers.
From corollary (1) and theorem (2) we see that
it is no coincidence that the area of the ![]() triangle, the
smallest Pythagorean triangle, is
triangle, the
smallest Pythagorean triangle, is
![]() , the smallest perfect
number.
, the smallest perfect
number.
Let ![]() be a positive integer such that
be a positive integer such that ![]() is a prime
(Mersenne prime). And let
is a prime
(Mersenne prime). And let
![]() be a primitive
Pythagorean triangle. Then, as table (4) shows, the area
be a primitive
Pythagorean triangle. Then, as table (4) shows, the area
![]() is a multiple of the perfect number
is a multiple of the perfect number
![]()
Examples
Consider the two primitive Pythagorean triangles
![]() and
and
![]() In this case
In this case ![]()
Since
![]() is a prime, we know that each area must be
a multiple of the perfect number
is a prime, we know that each area must be
a multiple of the perfect number
![]() And
indeed,
And
indeed,
![]() and
and
![]()
Consider the two primitive Pythagorean triangles
![]() and
and
![]() In this case
In this case ![]()
Since
![]() is a prime, we know that each area must be
a multiple of the perfect number
is a prime, we know that each area must be
a multiple of the perfect number
![]() And
indeed,
And
indeed,
![]() and
and
![]()
Consider the two primitive Pythagorean triangles
![]() and
and
![]() In this case
In this case ![]()
Since ![]() is a prime, we know that each area must be a
multiple of the perfect number
is a prime, we know that each area must be a
multiple of the perfect number
![]() And
indeed,
And
indeed,
![]() and
and
![]()
Note: Since
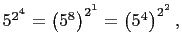
![]() is also a multiple of each of 6 and
28.
is also a multiple of each of 6 and
28.
That is,
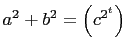 is a primitive Pythagorean
triangle where
is a primitive Pythagorean
triangle where